こんにちは!
前回こんな記事を書きました↓

本記事は『Pythonで物理シミュレーションをしよう!』シリーズの”Day4”です!
Contents
前回までに学んだこと
”Day3”の記事では「地面に反発する猫」の物理シミュレーションを実践しました。

本記事では「トランポリン(柔らかい地面)で弾む猫」の物理シミュレーションを実践します。

「トランポリンで弾む猫」をキラキラした瞳で見つめる”くるる”ちゃんが今日も可愛い(*・ω・)ノ♪
【Day4】Pyxelで物理シミュレーション
うーん。。


”Day3”記事で説明した”反発”は反発係数を使って速度が変化する物理シミュレーションでした。
今回は”トランポリンのばね”により、猫に加わる力が変化する物理シミュレーションです。
正解!
【復習】ばねの特性と復元力
“ばねの特性”については、以下の記事で説明済みです。

大正解!なので、本記事では復元力の概要のみ説明します。

”Day1”の記事で説明した通り、猫には重力という力が加わっています。
また、”ばね”には縮んだり・伸びたりしたとき、元に戻ろうとする復元力という力が発現します。この復元力は『フックの法則』より、算出することができます。
【フックの法則】
F = k・x(復元力:F, 自然長からの長さ:x, ばね定数:k)
技術や知識の積み重ねが大事です!
物理シミュレーション -復元力-
次は、トランポリン(復元力)の物理シミュレーションを考えてみます。
総復習
本記事の内容は、”Day1~Day3”記事で学んだ知識を総動員します!
Pythonで物理シミュレーションをしよう!-Day1-
物理(力学)の基礎を学び、物理シミュレーションの『雛形ソースコード』を使って自由落下運動の物理シミュレーションをPyxelでアニメーション化する

Pythonで物理シミュレーションをしよう!-Day2-
猫と地面(物体同士)の当たり判定を学び、物体同士が衝突した後の物理シミュレーションを実践

Pythonで物理シミュレーションをしよう!-Day3-
物体同士が衝突して反発する物理シミュレーションを実践

”Day1~Day3”記事の内容を理解できていれば、以降の説明もスムーズに理解できます。まだ、”Day1~Day3”記事を読んでいない人は先に読むことをオススメします!
大正解!
トランポリンの物理シミュレーション -当たり判定-
「トランポリン」≒「ばね」というイメージで話を進めます。
”Day1~Day3”までは猫と地面との当たり判定でしたが、今回は猫とばねとの当たり判定です。
ただし、猫が当たる対象が地面でもばねでも当たり判定の条件式は同じなので、今まで使ってきた以下の【当たり判定のソースコード】を流用することができます。
|
1 2 3 4 |
if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): # トランポリンに当たったときの処理(着地したときの処理) |
なので、本記事ではトランポリンに当たったときの処理のみを考えます。
テストで高得点とってお仕舞!とせずに…
- 学んだ知識がどこで活かせるか?
- この課題は過去に修得した知識や技術で解決できないか?
などを考えられるフクロウになってほしいです!

”くるる”ちゃんのモチベーションは今日も大樹のように高い!!
過去に開発したソフトウェアやネット上で公開しているソースコードを参考にして、効率良く作業できると良いですね
トランポリンの物理シミュレーション -衝突後の処理-
続いて、猫とトランポリンが当たったときの処理を考えてみます。
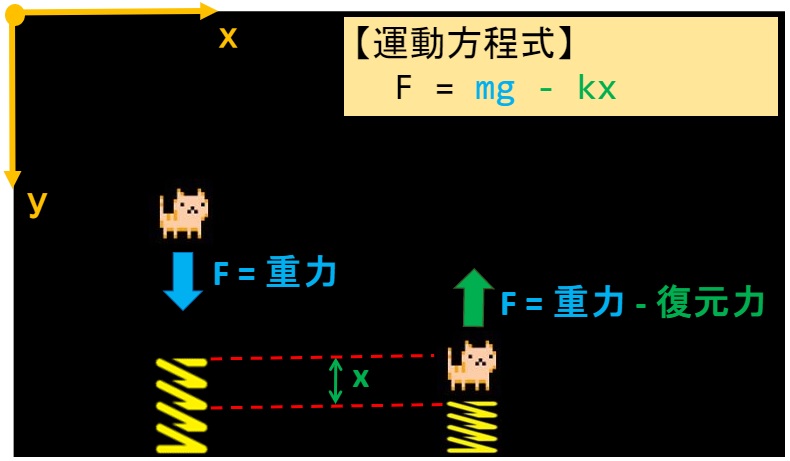
猫には常に”重力”が加わっていますが、ばねに当たったときは復元力も加わります。
数式に落とし込んでみます。
【重力の運動方程式】
f1 = m・g (質量:m[kg], 重力加速度g[m/s^2])
【復元力の運動方程式】
f2 = k・x (ばね定数:k[N/m], 変位x[m])
【トランポリンに当たったときの運動方程式】
F = f1 – f2
F = m・g – k・x
※y軸の向きに注意
|
1 2 3 4 5 6 7 8 9 10 |
# f = m * g (自由落下) f = self.Cats[i].weight * G # トランポリンに衝突 if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): x = self.Cats[i].pos.y + CAT_H - self.ground.pos1.y # f = m * g - k * x (重力 - 復元力) f += -K * x |
正解!今回はパラメータ定義を以下のように設定しています。
【各パラメータ】
- 猫の質量:m = 1 [kg]
- 重力加速度:g = 9.8 [m/s^2]
- ばね定数:k = 10 [N/m]
繰り返しですが、トランポリンに当たっているときに、猫に加わる力は以下の式で算出できます。
【トランポリンに当たったときの運動方程式】
F = m・g – k・x
以下の式に各パラメータを代入して…
【トランポリンに当たったときの運動方程式】
F = m・g – k・x
F = 1*9.8 – 10・x
猫に力が加わっていない状態(F = 0)なら、猫は静止するはずなので…
0 = 1*9.8 – 10・x
10・x = 9.8
x = 0.98
変位がx = 0.98で静止する!
はやぶさ先生の出題は「猫が弾むときの最小変位xを求めること」です。
つまり、『復元力 > 重力』を求めて猫に上向きかかる力の境界条件を求める!
10・x > 9.8
x > 0.98
できた!変位xが0.98より大きいときに猫が弾む!
最近、三歳になった”くるる”ちゃん天才なのでは?
少し補足すると本シリーズの物理シミュレーションでは「1pixel = 1m」でアニメーション化しています。
つまり、猫が1[pixel]でもトランポリンに食い込めば弾むようにk=10[N/m]を設定しました。

- 慌てないで!一つずつ丁寧に理解していきましょう!
- 基礎から”しっかり”理解できれば、応用もできます!!
- くるるちゃんのように本記事で楽しく物理を勉強してほしい!!!
最終的に完成したソースコード -トランポリンで弾む猫-
最終的に完成した「トランポリンで弾む猫」のソースコードが以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
import pyxel # ====== Image parameters ====== WINDOW_H = 120 WINDOW_W = 160 CAT_H = 16 CAT_W = 16 # ===== Physical parameters ===== FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] K = 10 # ばね定数 [N/m] class Vec2: def __init__(self, x, y): self.x = x self.y = y class cat: def __init__(self, img_id): self.pos = Vec2(0, 0) self.vec = 0 self.vel = 0 self.weight = 1 self.time = 0 self.img_cat = img_id def update(self, x, y, dx): self.pos.x = x self.pos.y = y self.vec = dx class Ground: def __init__(self): self.pos1 = Vec2(30, WINDOW_H - 20) self.pos2 = Vec2(WINDOW_W - 30, WINDOW_H) self.color = 14 # pink class App: def __init__(self): self.IMG_ID0_X = 60 self.IMG_ID0_Y = 65 self.IMG_ID0 = 0 self.IMG_ID1 = 1 # self.IMG_ID2 = 2 pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel") pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png") pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png") pyxel.mouse(True) # make instance self.Cats = [] self.ground = Ground() # self.mouse_count = 0 pyxel.run(self.update, self.draw) def update(self): if pyxel.btnp(pyxel.KEY_Q): pyxel.quit() # ====== ctrl cat ====== if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON): new_cat = cat(self.IMG_ID1) new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec) self.Cats.append(new_cat) cat_count = len(self.Cats) for i in range(cat_count): if self.Cats[i].pos.y < WINDOW_H: # f = m * g (自由落下) f = self.Cats[i].weight * G # トランポリンに衝突 if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): x = self.Cats[i].pos.y + CAT_H - self.ground.pos1.y # f = m * g - k * x (重力 - 復元力) f += -K * x # a = f / m (ニュートンの運動方程式) alpha = f / self.Cats[i].weight # v += a * dt (積分:加速度 ⇒ 速度) self.Cats[i].vel += alpha * DT # y += v * dt (積分:速度 ⇒ 位置) self.Cats[i].pos.y += self.Cats[i].vel * DT # 経過時間 self.Cats[i].time += DT # debug print("Cat No.", i) print("v = ", self.Cats[i].vel) print("y = ", self.Cats[i].pos.y) print("f = ", f) # Cat update self.Cats[i].update(self.Cats[i].pos.x, self.Cats[i].pos.y, self.Cats[i].vec) else: del self.Cats[i] break def draw(self): pyxel.cls(0) pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16) pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16) # ======= draw cat ======== for cats in self.Cats: pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5) # ======= draw ground ======== pyxel.rect(self.ground.pos1.x, self.ground.pos1.y, self.ground.pos2.x, self.ground.pos2.y, self.ground.color) App() |
”Day1~Day3”の記事で作成したソースコード同様、画像上の任意の位置でマウス左クリックすると猫が自由落下する物理シミュレーションを楽しめます(*・ω・)ノ♪
高い位置から落下させたとき、低い位置から落下させたときに「猫がどんな運動をするのか?」を観測してみてくださいね。
おわりに
『Pythonで物理シミュレーションをしよう!Day4 -復元力-』について説明しました。
pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本記事を書きあげました。
本記事をきっかけに「物理」や「プログラミング」に興味をもってくれる人が増えたら最高に嬉しいです!

(あ…いつもセリフとられた!笑)
”Day4” 完
次回予告(?)
『Pythonで物理シミュレーションしよう!』シリーズ記事ですが、次回が最終回になります。
”Day5”まで書けば、キリ良く「約1週間で完結するチュートリアル」といえるので!笑

お…おう!次回は…
分かった!次回の内容はシークレットにしよう(ソースコードが未完成だから公開できないわけじゃないよ…笑)
本記事楽しかったかな?次回もお楽しみに~