こんにちは！
以前『Pythonでレトロゲームを作ろう！』シリーズの記事を書きました。
というフクロウが目の前にいるので…
『Pythonで物理シミュレーションをしよう！』シリーズの記事を書こうと思います。
Contents
対象読者
Pyxelの使い方については、下記の記事で説明済みです。
という人は…
本シリーズ記事ではPyxelの基本的な使い方よりも「物理シミュレーション」の説明に注力します。
なので、本シリーズは以下の読者を想定して書きます。
【対象読者】
- Pythonで物理シミュレーションを学びたい人
- 物理シミュレーションをアニメーションで可視化したい人
- 数学・物理を学び、実践としてプログラミングまでしたい人
- （Pyxelの基本的な使い方が分かる人）
本シリーズでは「質点系の力学」を扱います。もっと複雑な物理シミュレーションを期待していた人には、ごめんなさい（今は力不足で書けないけど、いつかは…）
物理とは
ところで…
テーブルの上で静止するコップ、放物線を描く野球ボール、木から落ちるフクロウなど…あらゆる現象は「何らかの法則」に従って発現すると考えられています。
その「何らかの法則」を明らかにするのが”物理”という学問です。
力学とは
また、なぜ静止し続けるのか？なぜ動き続けるのか？なぜ木から落ちたのか？などを考えたとき…
「物体にどんな”力”が加わり、どんな運動をするのか？」という”力”に着目して現象を明らかにする学問が”力学”です。
正解！
大正解！！”くるる”ちゃんは賢いなぁ
ドヤ顔してる”くるる”ちゃんが今日も可愛い(*･ω･)ﾉ♪
物理を勉強すると”目に映る何気ない現象”を見るのがちょっと楽しくなるかも？（Hello, Physical World！）
物理シミュレーションとは
閃いた！
「繰り返し実施することが困難な現象」や値段が高いなど「何らかの理由で用意することが困難な物体の運動」を観測する場合…
物体の運動方程式を考え、その運動方程式を用いてシミュレーションすることで、現実世界の現象（物体の運動）をバーチャルで観測することができます。
泣き止んだ”くるる”ちゃんは勉強する気満々です！笑
- 物体の現象を数式化（モデル化）して物理シミュレーションを行います
- 物理シミュレーションにより、現実世界の現象を”再現”⇒”観測”することで、時間やコストを節約できます
- 実際には危険を伴う現象でもバーチャルなので安全に観測できます
ニュートンの運動則
物理…運動方程式……シミュレーション……
色んな勉強方法がありますが、今回は基礎から丁寧に学べるような説明にしますね(*･ω･)ﾉ♪
- 慣性の法則
物体に力が加わらない限り、静止している物体は静止し続け、運動している物体は等速直線運動を続ける - ニュートンの運動方程式
物体に加わる力は、物体の運動量の時間的変化に等しいため、以下の式で表現できる
F = m・a ( 単位 : [N] = [kg]・[m/s^2] ) - 作用・反作用
物体Aが物体BをFの力で押すとき、物体Aには-F（反対方向）の力が加わる
正解！どの法則も超重要だけど、今回は第二法則（ニュートンの運動方程式）がメインだね！
- 自分に合った勉強方法を見つけて下さいね
- ニュートンの運動則はどれも超重要です
ニュートンの運動方程式
ニュートンの運動方程式を私のなりの言葉で噛砕いて表現すると…
『質量m[kg]の物体に力F[N]が加わると、加速度a[m/s^2]が生じる』
となります。式変形すると分かりやすいです。
F = m・a ( 単位 : [N] = [kg]・[m/s^2] )
a = F / m ( 単位 : [m/s^2] = [N] / [kg] )
数式の意味を理解することが重要だよ！
無言の敬礼がカッコイイぞ！
数式の”成り立ち”や”意味”に興味を持ってほしい！
加速度・速度・位置の関係と微分積分
えーと…ニュートンの運動方程式によると…
おしい！正確には”6Nの力を加え続けると”だね！
加速度をグラフで表現すると以下のようになります。
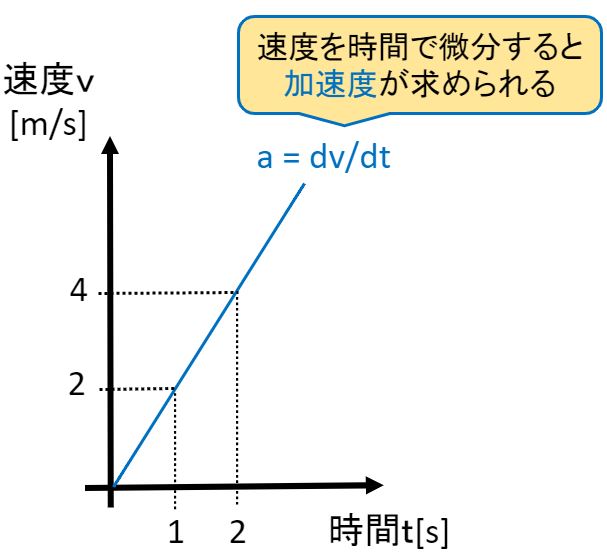加速度が２というのは、時間が１s経過する毎に速度が２ずつ増加するという意味です。
つまり、速度と時間のグラフの傾きが加速度です。
そして、傾きは速度dvを微小時間dtで割った以下の式で表現できます。
a = dv / dt ( 単位 : [m/s^2] = [m/s] / [s] )
正解！
大正解！！
- 位置を時間で微分したものが速度
v = dx/dt ( 単位：[m/s] = [m] / [s] ) - 速度を時間で微分したものが加速度
a = dv/dt ( 単位 : [m/s^2] = [m/s] / [s] )
また、加速度は位置を二階微分したものとも言えますね。
同様に積分についても確認しておきましょう！
- 加速度を積分したものが速度
v = ∫a・dt ( 単位：[m/s] = [m/s^2] * [s] ) - 速度を積分したものが位置
x = ∫v・dt ( 単位 : [m] = [m/s] * [s] )
猛禽類ジョーク！！
- 単位から数式の成り立ちを理解できる場合があります
- 繰り返す！数式の”成り立ち”や”意味”に興味を持ってほしい！
物理シミュレーションのフロー
えーと…
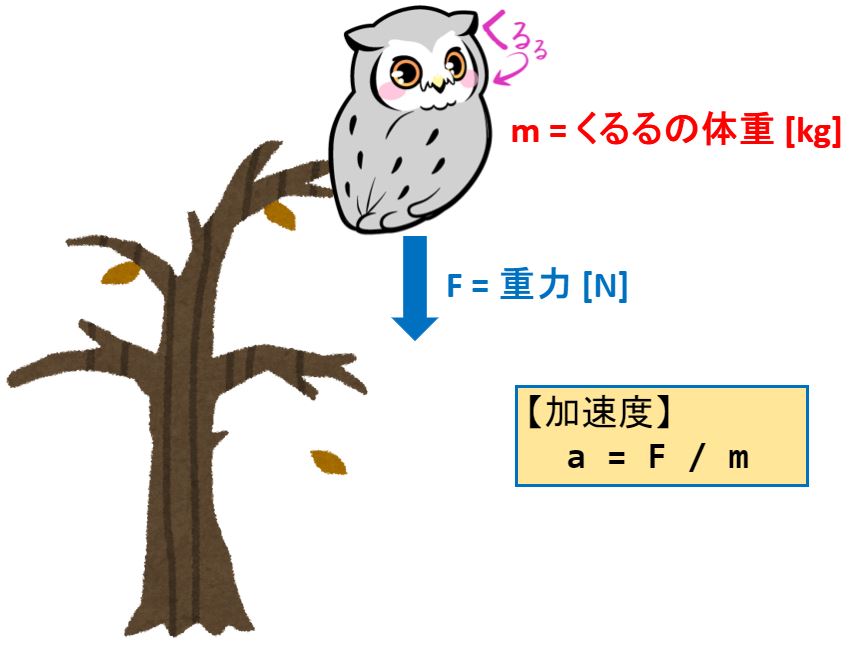体重0.2kgの”くるる”に重力という力が加わっていて…
【ニュートンの運動方程式】
a = F / m
ニュートンの運動方程式から加速度を求められる…
加速度を積分したら速度、速度を積分したら位置が求められるから…
物理シミュレーションのフローはこんな感じだね！
【物理シミュレーションのフロー】
- 物体に加わる力を求める
- ニュートンの運動方程式から加速度を求める
- 加速度を積分して速度を求める
- 速度を求めて位置を求める
- ❶～❹を繰り返す
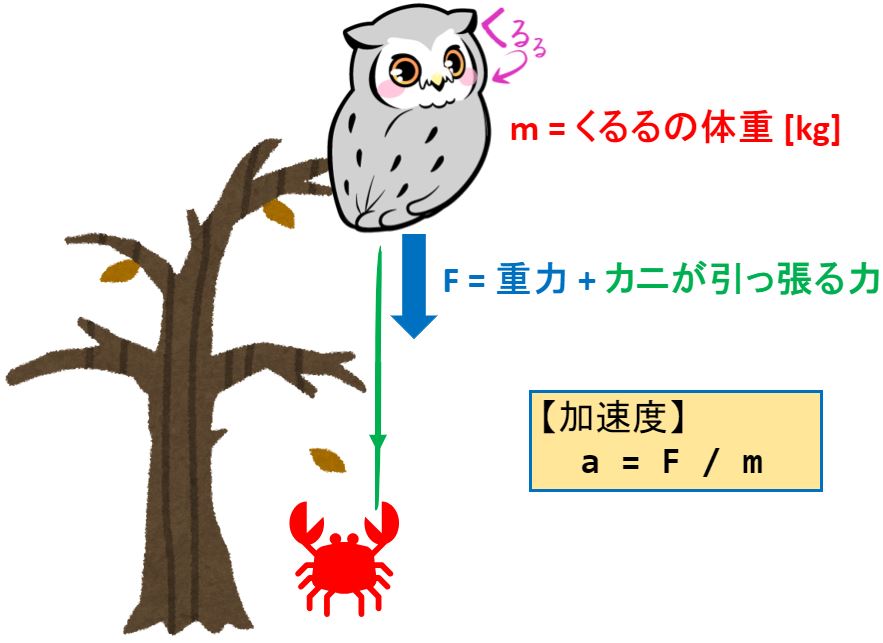
少しだけ補足すると、”くるる”ちゃんに加わる下向きの力の合計”F”から加速度を求めるので、”F”の式は以下の通りです。
【くるるに加わる下向きの力】
f1 = 重力
f2 = カニが引っ張る力
…
fn = ???な力
【全ての力の合計値”F”】
F = f1 + f2 + … fn
ただし、今回は”くるる”に加わった力が”重力”のみとします。また、重力は質量mと重力加速度ｇの掛け算で求められます。
F = f1
F = 重力
F = m・g ( 単位 : [N] = [kg] * [m/s^2] )
※本記事では重力加速度g = 9.8とします
猛禽類ジョーク！！
- 繰り返す！「物体にどんな”力”が加わり、どんな運動をするのか？」という”力”に着目して現象を明らかにする学問が”力学”です
- 物体に加わる”力”の向きと大きさに着目しましょう
- 力⇒加速度⇒速度⇒位置の演算結果に基づき物理シミュレーションを行います
【Day1】Pyxelで物理シミュレーション
今までの説明が物理（力学）の基礎になります。以降からは、本題の『Pythonで物理シミュレーション』を実践していきます！
今までのところをもう一度読み返すも良し！休憩するのも良し！すぐに先に進むのも良しです！
物理シミュレーションの雛形ソースコード
物理シミュレーションのフローは以下の通りでしたね。
【物理シミュレーションのフロー】
- 物体に加わる力を求める
- ニュートンの運動方程式から加速度を求める
- 加速度を積分して速度を求める
- 速度を求めて位置を求める
- ❶～❹を繰り返す
これをPythonで実装したコードが以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] for i in range(n_count): # f = m * g （力） f = m * G # a = f / m （ニュートンの運動方程式） alpha = f / m # v += a * dt （積分：加速度 ⇒ 速度） vel += alpha * DT # y += v * dt（積分：速度 ⇒ 位置） y += vel * DT # 経過時間 time += DT |
これが物理シミュレーションの『雛形コード』になります。
汎用性の高い『雛形コード』は色んなところで大活躍します
ソースコードの解説❶ -フレームレート-
FPSは”frames per second”の略称で１秒間に処理できるフレーム数（画像数）のことだよ。
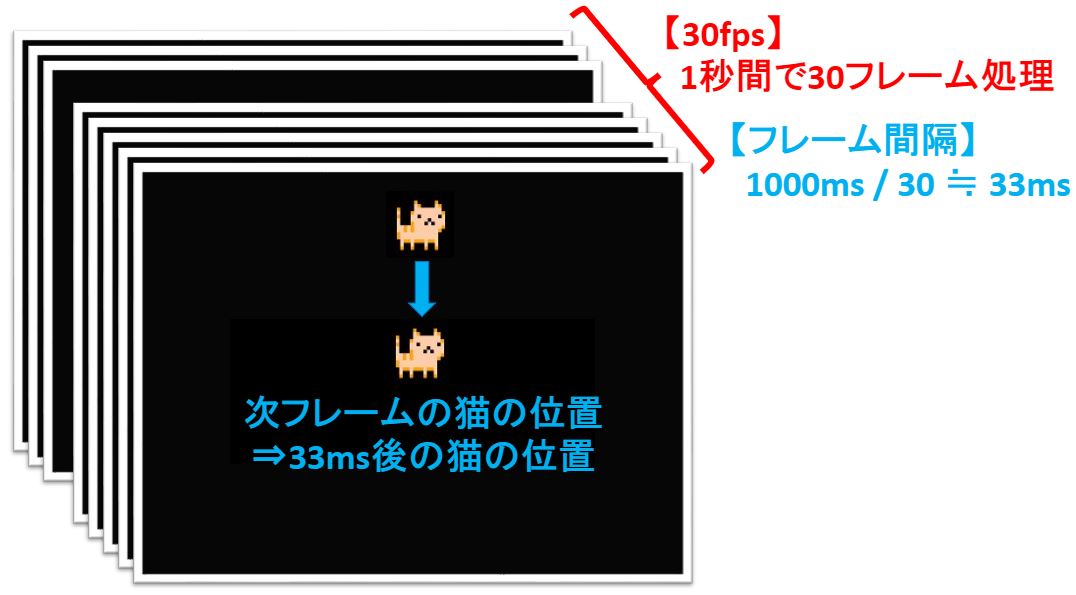
30fpsの場合は１秒間で30フレーム処理することになります。またフレーム間隔はfpsの逆数で求められます。
【フレーム間隔】
フレーム間隔 = 1 / fps ( 単位 : [s/f] = 1 / [f/s] )
ミリ秒で演算しても良いです(*･ω･)ﾉ♪
【フレーム間隔】
フレーム間隔 = 1000 / fps ( 単位 : [ms/f] = 1000[ms] / [f/s] )
30fpsの場合は33msecがフレーム間隔です。
つまり、猫が落下するアニメーション（物理シミュレーション）を考えたとき、次フレームには33msec後の落下位置に猫を描画すれば良いです。
正解！
ソースコードの解説❷ -基準と力の向き-
あれ？
F = 重力
F = -m・g ( 単位 : [N] = [kg] * [m/s^2] )
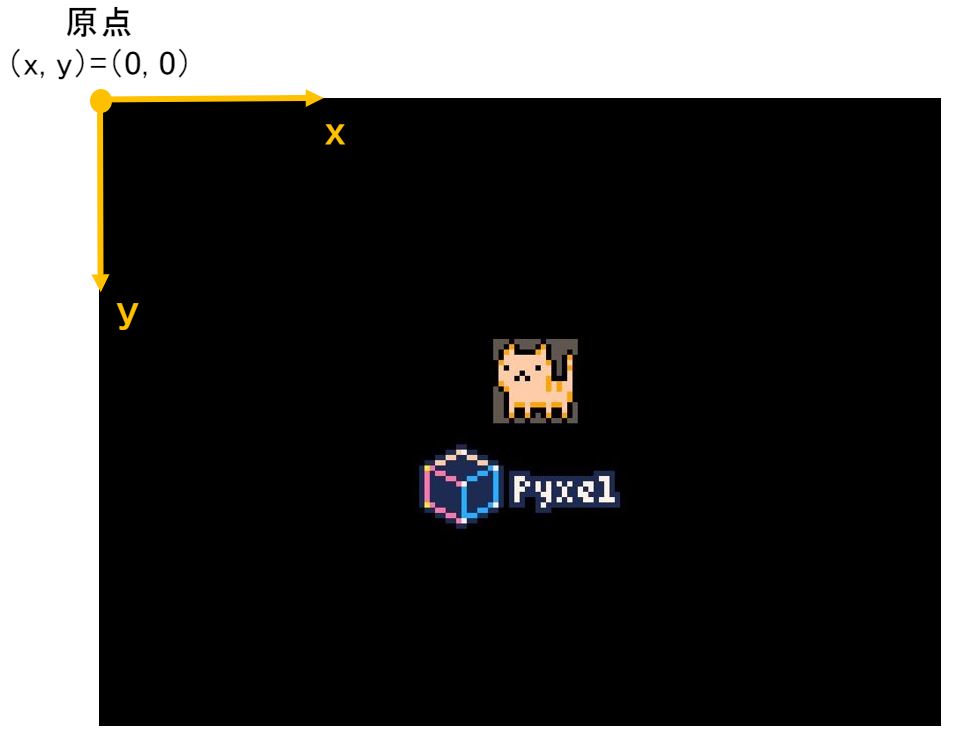
正解！”y軸の向き”と”力の向き”が同じならプラス、”反対向き”ならマイナスです。
たぶん”くるる”ちゃんは左下原点で説明している本かソースコードを読んだんじゃないかな？
原点を左下に設定してから、物理シミュレーションを行うことも多いので、”くるる”ちゃんの感覚は正しいよ。
ただ、基準を気にせず、下向きはマイナス・右向きはプラスみたいな覚え方は良くないかもしれないね。
最近、三歳になった”くるる”ちゃん天才なのでは？
- 基準軸の向きと力の向きが同じ：プラス方向の力
- 基準軸の向きと力の向きが反対：マイナス方向の力
最終的に完成したソースコード
”くるる”ちゃん最終的に完成させたソースコードはこちらです↓
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
import pyxel # ====== Image parameters ====== WINDOW_H = 120 WINDOW_W = 160 CAT_H = 16 CAT_W = 16 # ===== Physical parameters ===== FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] class Vec2: def __init__(self, x, y): self.x = x self.y = y class cat: def __init__(self, img_id): self.pos = Vec2(0, 0) self.vec = 0 self.vel = 0 self.weight = 1 self.time = 0 self.img_cat = img_id def update(self, x, y, dx): self.pos.x = x self.pos.y = y self.vec = dx class App: def __init__(self): self.IMG_ID0_X = 60 self.IMG_ID0_Y = 65 self.IMG_ID0 = 0 self.IMG_ID1 = 1 # self.IMG_ID2 = 2 pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel") pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png") pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png") pyxel.mouse(True) # make instance self.Cats = [] # self.mouse_count = 0 pyxel.run(self.update, self.draw) def update(self): if pyxel.btnp(pyxel.KEY_Q): pyxel.quit() # ====== ctrl cat ====== if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON): new_cat = cat(self.IMG_ID1) new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec) self.Cats.append(new_cat) cat_count = len(self.Cats) for i in range(cat_count): if self.Cats[i].pos.y < WINDOW_H: # f = m * g （力） f = self.Cats[i].weight * G # a = f / m （ニュートンの運動方程式） alpha = f / self.Cats[i].weight # v += a * dt （積分：加速度 ⇒ 速度） self.Cats[i].vel += alpha * DT # y += v * dt（積分：速度 ⇒ 位置） self.Cats[i].pos.y += self.Cats[i].vel * DT # 経過時間 self.Cats[i].time += DT # Cat update self.Cats[i].update(self.Cats[i].pos.x, self.Cats[i].pos.y, self.Cats[i].vec) else: del self.Cats[i] break def draw(self): pyxel.cls(0) pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16) pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16) # ======= draw cat ======== for cats in self.Cats: pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5) App() |
物理シミュレーションで遊ぼう！
作成したソースコード起動し、画像上の任意の位置でマウス左クリックすると猫が自由落下する物理シミュレーションを楽しめます(*･ω･)ﾉ♪
- マウス左クリックで猫インスタンス生成
- 猫が画面下端まで来ると、インスタンスを破棄
という仕様なので、画面外でもずーっと自由落下しているわけではないよ
カニ登場！
うーん。。
（メガ…なんだって？）
ソースコードの69行目にカニが引っ張る力を追加します。
|
1 2 |
# f = 重力 + カニが引っ張る力 f = self.Cats[i].weight * G + 10**6 |
物理シミュレーション結果↓
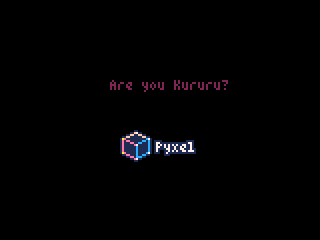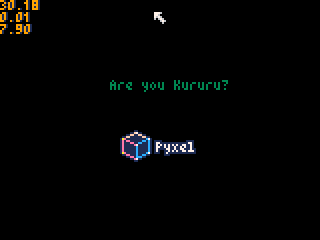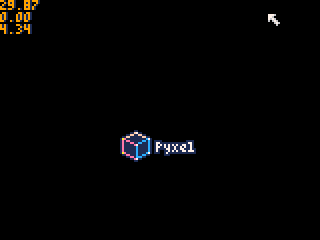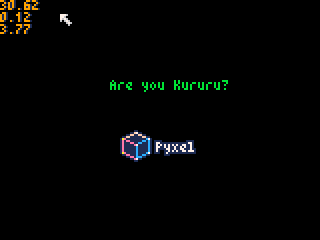
試しに10^4[N]に変更してみます。
|
1 2 |
# f = 重力 + カニが引っ張る力 f = self.Cats[i].weight * G + 10**4 |
物理シミュレーション結果↓
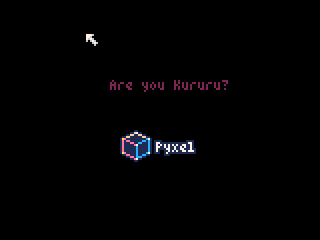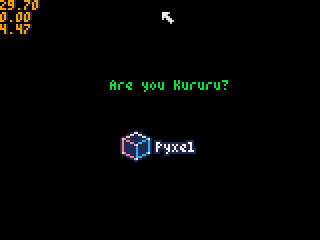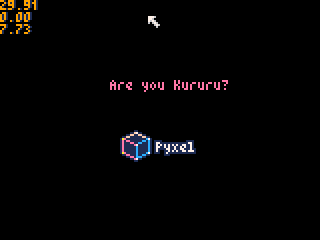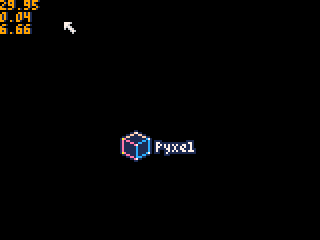
ソースコードを色々と改造して物理シミュレーションを楽しんで下さいね
おわりに
『Pythonで物理シミュレーションをしよう！Day1 -自由落下-』について説明しました。
pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本記事を書きあげました。
という人が少しでもいると嬉しいです。
次回予告
『Pythonで物理シミュレーションしよう！』シリーズ記事ですが、何記事書くかなどについて、あまり決めていません。
ただし、重要な基礎の部分は本記事にギュッと凝縮して書いています。
なので、本記事の内容を理解⇒応用することで様々な物理シミュレーションを実現できるようになります。
”くるる”ちゃんのように好奇心旺盛に色々な物理シミュレーションに挑戦して下さいね！
さっそく好奇心旺盛なフクロウがキラキラした目でお願いしてきた。
”くるる”ちゃん優しいな～
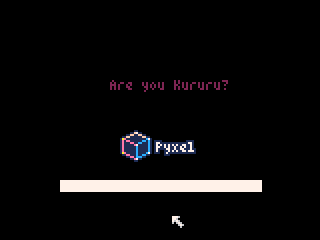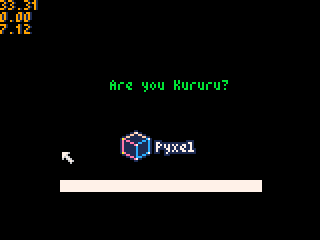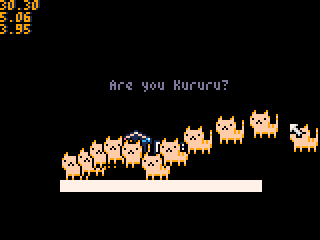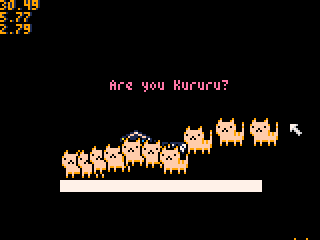
「地面に綺麗に着地する猫」と「地面に反発する猫」
本記事楽しかったかな？次回もお楽しみに～
