こんにちは!
前回こんな記事を書きました↓

本記事は『Pythonで物理シミュレーションをしよう!』シリーズの”Day2”です!
Contents
前回までに学んだこと
”Day1”の記事で以下のことを勉強しました。
- 物理(力学)の基礎
- 物理シミュレーションの『雛形ソースコード』の作り方
- 自由落下運動の物理シミュレーションをPyxelでアニメーション化
忘れている人や不安な人は、もう一度”Day1”の記事を読んでみてね(*・ω・)ノ♪
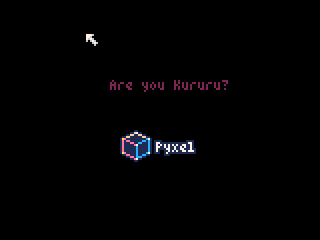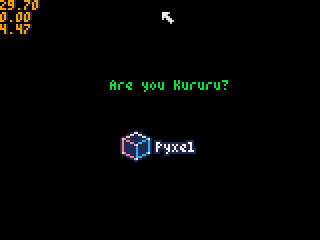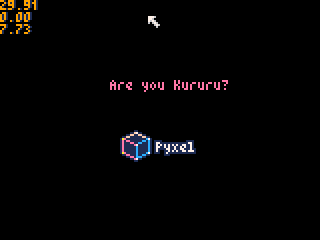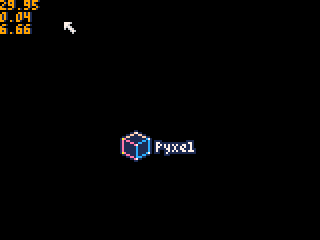
「自由落下する猫」と「下から強い力で引っ張られて落下する猫」
”Day1”の記事を読めば、自分の好きな”キャラ”で自由落下運動を実践できるようになります!
【Day2】Pyxelで物理シミュレーション
”Day1”の記事では自由落下させて終了でしたが、本記事では着地させます。
「地面に綺麗に着地する猫」と「地面に反発する猫」
大丈夫!本記事で丁寧に解説するし、以下の記事を読んだ”くるる”ちゃんなら「地面に綺麗に着地する猫」のプログラムはもう作れるはずだよ!


くるるちゃんは何か閃いたようです!
勉強は積み重ねが大事です。頑張って学んだ”過去”の自分が”現在”や”未来”の自分を助けてくれる日が必ずきますよ
猫と地面の当たり判定
最初に猫と地面の座標を確認します。
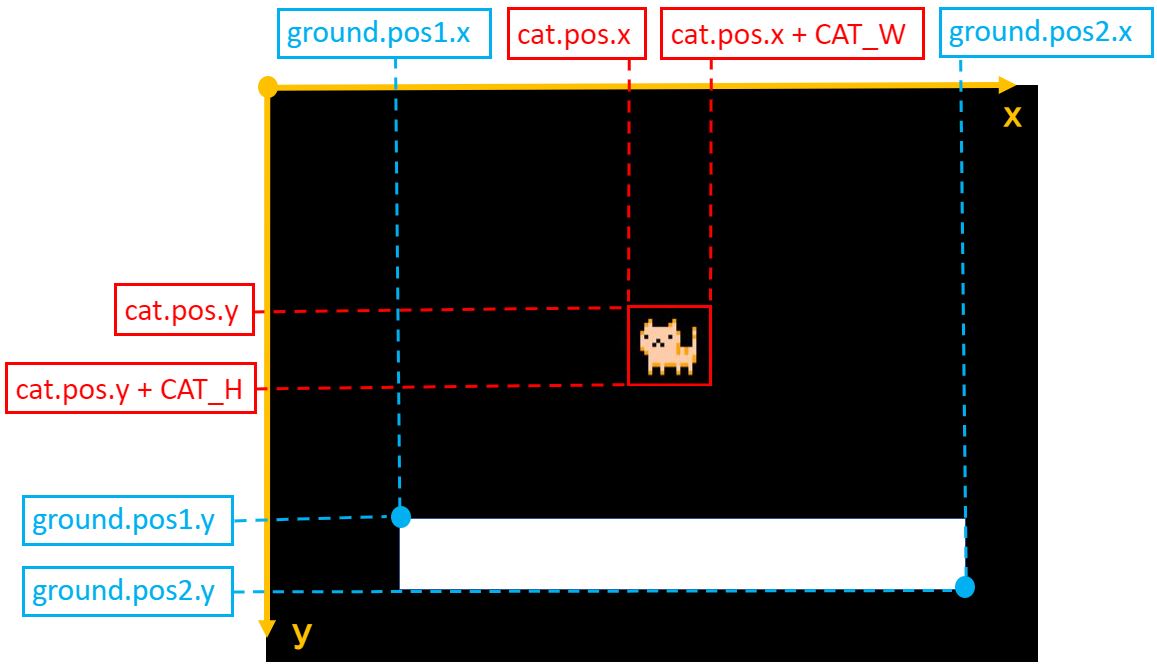
猫が落下する・しないは猫と地面の当たり判定で考えることができます。
【猫が落下】
猫の足が地面よりも上にある状態(地面に当たっていない)
【猫が着地】
猫の足が地面に接触あるいは地面に足が埋まる状態(地面に当たっている)
これを数式に落とし込むと…
【猫が落下】
self.Cats[i].pos.y + CAT_H < ground.pos1.y
【猫が着地】
ground.pos1.y <= self.Cats[i].pos.y + CAT_H
※y軸が下方向なことに注意
【猫が着地】の式が”当たり判定”の条件式になります。
画面の左端から右端まで地面が続いている場合、上記の条件式のみで良いのですが、今回は右端と左端に隙間がある地面を扱います。
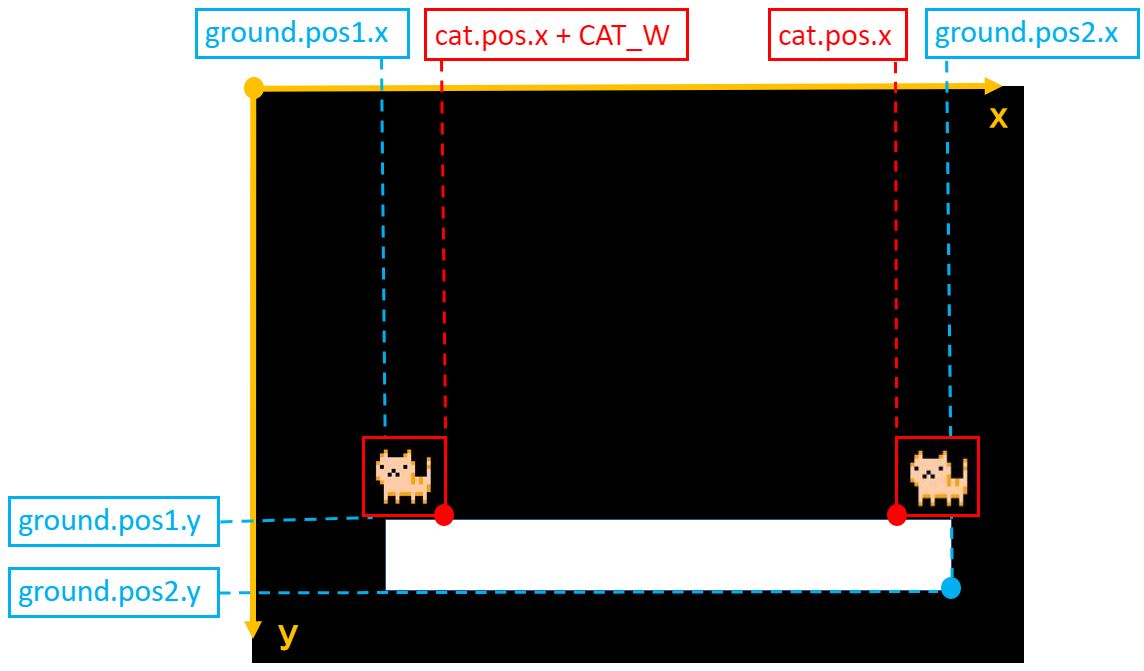
さきほど同様、猫が地面より下に落下する・しないは猫と地面の当たり判定で考えることができます。
【猫が地面より下に落下】
猫が地面の外側にいる状態(地面に当たっていない)
【猫が着地】
猫が地面の内側にいる状態(地面に当たっている)
これを数式に落とし込むと…
【猫が地面より下に落下】
Cats[i].pos.x + CAT_W < ground.pos1.x
かつ
ground.pos2.x < Cats[i].pos.x
【猫が着地】
ground.pos1.x <= Cats[i].pos.x + CAT_W
かつ
Cats[i].pos.x <= ground.pos2.x
【猫が着地】の式が”当たり判定”の条件式になります。
以上から、猫と右端および左端に隙間がある地面との当たり判定は以下のよう表現できます。
【猫が着地】
猫の足が地面に接触あるいは地面に足が埋まる状態
かつ
猫が地面の内側にいる状態
これを数式に落とし込むと…
【猫が着地】
ground.pos1.y <= self.Cats[i].pos.y + CAT_H
かつ
ground.pos1.x <= Cats[i].pos.x + CAT_W
かつ
Cats[i].pos.x <= ground.pos2.x
|
1 2 3 4 |
if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): # 地面に当たったときの処理(着地したときの処理) |
正解!
以下の記事で『当たり判定』を勉強済みの”くるる”ちゃんは”スッと”理解できたようです。

シューティングゲームなどにも使われる『当たり判定』について、もっと勉強したい人は『Pythonでレトロゲームを作ろう!Day 6-当たり判定-』の記事を読んでみてね(*・ω・)ノ♪
繰り返す!勉強は積み重ねが大事です
物理シミュレーション -地面に綺麗に着地-
猫と地面との『当たり判定』の条件式まで説明しました。
次は、地面に当たったときの処理(着地したときの処理)を考えてみます。

「猫が地面に綺麗に着地した」というのが、どんな現象(どんな状態)なのか?を考えてみます。
”くるる”ちゃん…すごい!
ただ、「着地した瞬間の衝撃を猫が吸収して…」というのをシミュレーションするのは、とても難しいので、「静止状態になった」という現象だけを再現します。
つまり、猫が地面に当たったとき”猫の落下速度=0”にすれば良いです。
|
1 2 3 4 5 |
# 地面に衝突 (綺麗に着地:速度 = 0) if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): self.Cats[i].vel = 0 |
正解!
最終的に完成したソースコード -地面に綺麗に着地-
最終的に完成した「猫が地面に着地する物理シミュレーション」のソースコードが以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 |
import pyxel # ====== Image parameters ====== WINDOW_H = 120 WINDOW_W = 160 CAT_H = 16 CAT_W = 16 # ===== Physical parameters ===== FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] class Vec2: def __init__(self, x, y): self.x = x self.y = y class cat: def __init__(self, img_id): self.pos = Vec2(0, 0) self.vec = 0 self.vel = 0 self.weight = 1 self.time = 0 self.img_cat = img_id def update(self, x, y, dx): self.pos.x = x self.pos.y = y self.vec = dx class Ground: def __init__(self): self.pos1 = Vec2(30, WINDOW_H - 15) self.pos2 = Vec2(WINDOW_W - 30, WINDOW_H - 10) self.color = 7 # white class App: def __init__(self): self.IMG_ID0_X = 60 self.IMG_ID0_Y = 65 self.IMG_ID0 = 0 self.IMG_ID1 = 1 # self.IMG_ID2 = 2 pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel") pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png") pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png") pyxel.mouse(True) # make instance self.Cats = [] self.ground = Ground() # self.mouse_count = 0 pyxel.run(self.update, self.draw) def update(self): if pyxel.btnp(pyxel.KEY_Q): pyxel.quit() # ====== ctrl cat ====== if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON): new_cat = cat(self.IMG_ID1) new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec) self.Cats.append(new_cat) cat_count = len(self.Cats) for i in range(cat_count): if self.Cats[i].pos.y < WINDOW_H: # f = m * g (力) f = self.Cats[i].weight * G # a = f / m (ニュートンの運動方程式) alpha = f / self.Cats[i].weight ''' # a = g (加速度) alpha = G ''' # v += a * dt (積分:加速度 ⇒ 速度) self.Cats[i].vel += alpha * DT # 地面に衝突 (綺麗に着地:速度 = 0) if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): self.Cats[i].vel = 0 # y += v * dt(積分:速度 ⇒ 位置) self.Cats[i].pos.y += self.Cats[i].vel * DT # 経過時間 self.Cats[i].time += DT # Cat update self.Cats[i].update(self.Cats[i].pos.x, self.Cats[i].pos.y, self.Cats[i].vec) else: del self.Cats[i] break def draw(self): pyxel.cls(0) pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16) pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16) # ======= draw cat ======== for cats in self.Cats: pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5) # ======= draw ground ======== pyxel.rect(self.ground.pos1.x, self.ground.pos1.y, self.ground.pos2.x, self.ground.pos2.y, self.ground.color) App() |
”Day1”の記事で作成したソースコード同様、画像上の任意の位置でマウス左クリックすると猫が自由落下する物理シミュレーションを楽しめます(*・ω・)ノ♪
おわりに
『Pythonで物理シミュレーションをしよう!Day2 -衝突-』について説明しました。
pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本記事を書きあげました。

冒頭で紹介した「地面に反発する猫」の物理シミュレーションについても説明したかったのですが…
意外と本記事のボリュームが多くなってしまったので、次回”Day3”の記事で説明しますね。
どうすれば、「反発する猫」のシミュレーションを実装できるか考えるのも面白いですよ(*・ω・)ノ♪
余裕がある人は自作してみて、”Day3”の記事で答え合わせするのも良いですね!

夢中でプログラミングしている”くるる”ちゃんが今日も可愛い!
本記事楽しかったかな?次回もお楽しみに~