【Pyxel】Pythonで物理シミュレーションをしよう！ Day 5 -復元力２-

こんにちは！

くるる

人気フクロウの”くるる”@kururu_owl だよー

はやぶさ

現役エンジニアの”はやぶさ”@Cpp_Learningです

前回こんな記事を書きました↓

【Pyxel】Pythonで物理シミュレーションをしよう！ Day 4 -復元力-こんにちは！前回こんな記事を書きました↓ https://cpp-learning.com/pyxel_p...

本記事は『Pythonで物理シミュレーションをしよう！』シリーズの”Day5”です！

くるる

本記事が最終回だよー。このシリーズが終わっちゃうのは悲しいけど、最後まで楽しく勉強するぞー♪

はやぶさ

あっ！最終回のことだけど…まぁ本記事の最後にお知らせします。今日も楽しく物理シミュレーションを実践しましょう！

くるる

（この流れはもしや…？）

Contents

1 前回までに学んだこと
2 【Day5】Pyxelで物理シミュレーション
3 バンジーの物理シミュレーション
4 最終的に完成したソースコード -バンジージャンプ猫-
5 おわりに
6 次回予告

前回までに学んだこと

”Day４”の記事では「トランポリンで弾む猫」の物理シミュレーションを実践しました。

くるる

トランポリンで遊ぶ猫がとても可愛い♪

本記事では「バンジージャンプする猫」の物理シミュレーションを実践します。

くるる

スパイダーマンみたい！笑

…え？スパイダーマン！？

街中を蜘蛛の糸で飛び回るスパイダーマンと伸縮するロープで”びよんびよん”する猫が”くるる”ちゃんの中ではリンクしたようです！笑

ヒーロー大好きな３歳児の”くるる”ちゃんが今日も可愛い(*･ω･)ﾉ♪

【Day5】Pyxelで物理シミュレーション

くるる

「トランポリン」と「伸縮するロープ」ってどちらも”ばねの特性”がある気がする！

正解！

”Day４”記事では猫がトランポリンに当たったときに、ばねの特性（復元力）で弾んでいました。

今回のバンジーは最初から猫がロープ（ばね）に繋がれている状態の物理シミュレーションです。

くるる

”ばねの特性”を理解したら、トランポリン・バンジー両方の物理シミュレーションができるようになる！？

大正解！”ばねの特性”は物理の基礎ですが、基礎をしっかり修得していれば、あらゆる対象の物理シミュレーションが自作のソースコードで実現できますよ！

くるる

基礎力アップしたい！

はやぶさ

基礎力アップしたい！

応用技術に注目しがちですが、基礎をしっかり修得し、応用も創造できる『骨太な技術者』になりたいですね(*･ω･)ﾉ♪

基礎が大事！

バンジーの物理シミュレーション

”くるる”ちゃんが黒板に何かを書き始めました！

くるるの技術ノート

トランポリ：”復元力”で猫が弾む
バンジー：”復元力”でロープが伸縮
どちらも”復元力”という力による現象

くるる

はやぶさ先生のヒントのおかげで、ソースコード自作できそう！

はやぶさ

じゃあ、以降の説明は”くるる”ちゃんに任せて良いかな？

くるる

任せて―

マインドマップ・テキスト・グラフ・イラストなど、脳内にあるイメージを何らかの形で可視化すると、頭の中が整理できますよ

【復習】トランポリンと復元力

くるる

まずは復習からいくよー

”Day４”の記事で勉強したトランポリンは以下のイメージだったよね♪

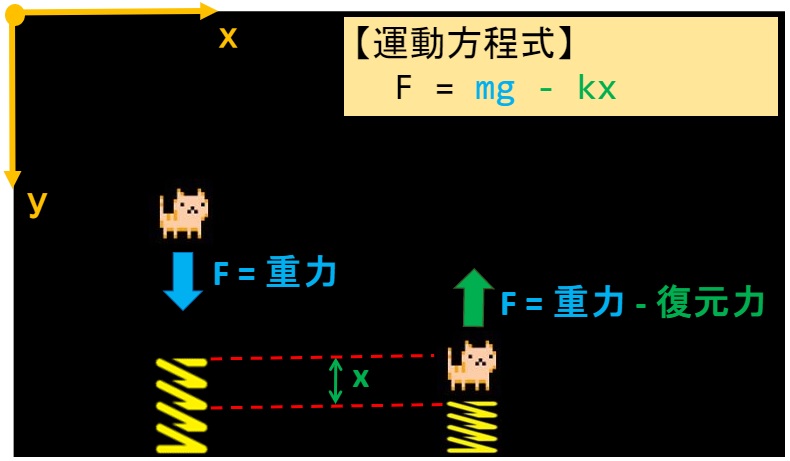
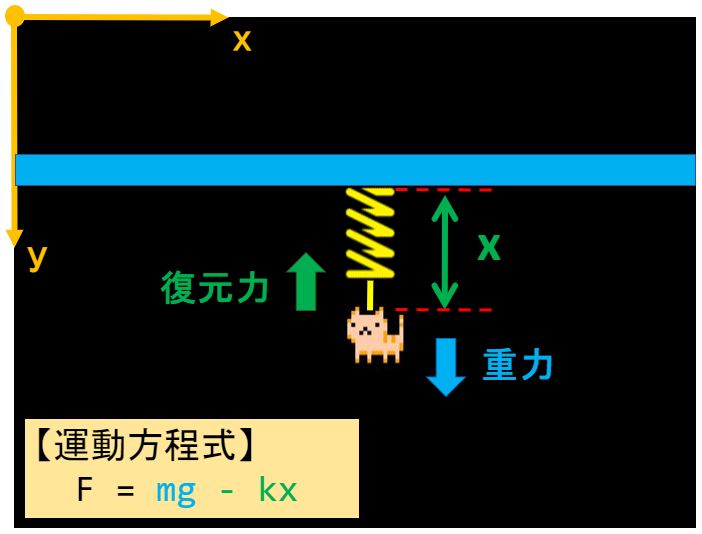
猫には常に”重力”が加わっているけど、ばねに当たったときには復元力も加わる！

これを数式に落とし込んでみるる(*･ω･)ﾉ♪

【重力の運動方程式】

f1 = m・g　(質量：m[kg], 重力加速度g[m/s^2])

【復元力の運動方程式】

f2 = k・x　(ばね定数：k[N/m], 変位x[m])

【トランポリンに当たったときの運動方程式】

F = f1 – f2

F = m・g – k・x

※y軸の向きに注意

最後はソースコードに落とし込む！

# f = m * g （自由落下）
f = self.Cats[i].weight * G

# トランポリンに衝突
if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H)
 and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W)
 and (self.Cats[i].pos.x <= self.ground.pos2.x)):
    x = self.Cats[i].pos.y + CAT_H - self.ground.pos1.y
    # f = m * g - k * x （重力 - 復元力）
    f += -K * x

# f = m * g （自由落下）

f = self.Cats[i].weight * G

# トランポリンに衝突

if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H)

and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W)

and (self.Cats[i].pos.x <= self.ground.pos2.x)):

x = self.Cats[i].pos.y + CAT_H - self.ground.pos1.y

# f = m * g - k * x （重力 - 復元力）

f += -K * x

はやぶさ

前回学んだことをしっかり説明できています！素晴らしい！

InputするだけでなくOutputすることが知識や技術を習得するための近道だと感じています。人に説明するも良し！本サイトのソースコードを改良するも良しです！楽しく”Input ⇒ Output”を実践して下さいね

バンジーロープと復元力

くるる

本題いくよー

本記事の前半で”はやぶさ先生”が以下のヒントをくれました

はやぶさ

今回のバンジーは最初から猫がロープ（ばね）に繋がれている状態の物理シミュレーションです。

このヒントに基づいて、絵を描いてみます。

”Day４”の記事で勉強したトランポリンと違って、猫には常に重力と復元力が加わるので、条件分岐なしの以下の数式で表現できます。

【重力の運動方程式】

f1 = m・g　(質量：m[kg], 重力加速度g[m/s^2])

【復元力の運動方程式】

f2 = k・x　(ばね定数：k[N/m], 変位x[m])

【ばね変位】

x = Yc – Y　(猫のy座標 – 天井のy座標)

【バンジーの運動方程式】

F = f1 – f2

F = m・g – k・x

※y軸の向きに注意

最後はソースコードに落とし込む！

# ばね変位：x（猫のｙ座標 - 天井のｙ座標）
x = self.Cats[i].pos.y - self.ceiling.pos2.y
# f = m * g - k * x（重力 - 復元力）
f = self.Cats[i].weight * G - K * x

# ばね変位：x（猫のｙ座標 - 天井のｙ座標）

x = self.Cats[i].pos.y - self.ceiling.pos2.y

# f = m * g - k * x（重力 - 復元力）

f = self.Cats[i].weight * G - K * x

はやぶさ

大正解！くるるちゃんはしっかり基礎が身についてるよー

くるるちゃんと同じように自力で数式を算出できた人は、大変よくできました！まだ、難しいと感じる人は、自分のペースで良いので丁寧に理解していきましょう(*･ω･)ﾉ♪

くるるの失敗！？

くるる

あれ？間違えちゃったかも…

さきほどまで、自信満々だった”くるる”ちゃんが(´・ω・｀)な顔をしています。

はやぶさ

くるるちゃん！大丈夫だよ！さっきの数式で正解だよ。何が不安なのか教えてくれるかな？

うん。。

以下の絵は伸びた”ばね”が縮むときに発生する復元力が上方向（y軸と反対の向き）にのみ働くイメージで書いたの。

でも、このシミュレーション結果を見てみると…

“ばね”が天井よりも上に伸びてから縮むときは、下方向（y軸と同じ向き）の力が働くと思うの。

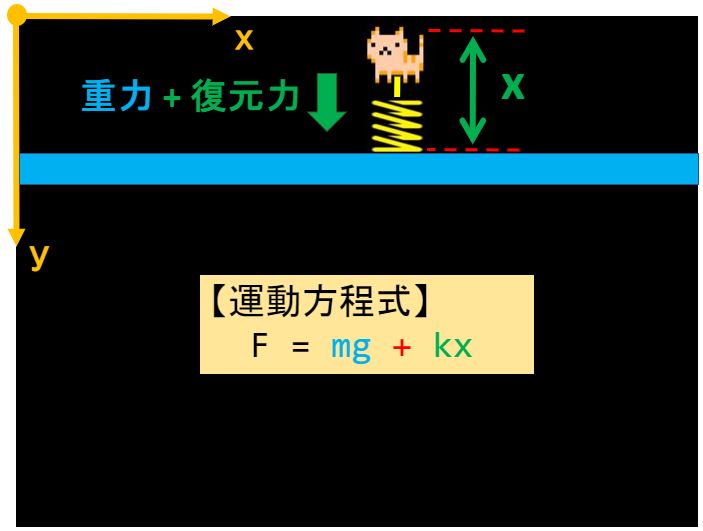
つまり、猫が天井より上か下かで条件分岐が必要だと思うの！

はやぶさ

あぁ…なるほど。。

はやぶさ

くるるちゃん”Day３”の記事で反発係数を自力で算出してたよね？今回も同じように具体的な数値を代入してみたらどうかな？

今回はパラメータ定義を以下のように設定しています。

【各パラメータ】

猫の質量：m = 1 [kg]
重力加速度：g = 9.8 [m/s^2]
ばね定数：k = 5 [N/m]
天井の位置（ｙ座標）：Y = 30[pixel]

※ 1m = 1pixel

猫が天井よりも下にいるときと上にいるときの”力の向き”を考えてみて下さい。

くるる

やってみる！

猫が天井よりも下にいるとき

天井の位置：Y = 30[pixel]で固定値だから、猫の位置：Ycが天井よりも下にいる状態は以下の通りです。

【猫が天井よりも下にいるときの条件式】

Y < Yc

30 < Yc

もし猫の位置：Yc = 40なら、ばね変位は以下の式で算出できます。

【猫が天井よりも下にいるときの”ばね変位”】

x ＝ Yc – Y

x ＝ 40 – 30

x ＝ 10

先ほど求めたバンジーの運動方程式に代入してみます。

【バンジーの運動方程式】

F = m・g – k・x

F = 1*9.8 – 5・10

F = 9.8 – 50

F = -40.2

F < 0

Fがマイナスになったので、くるるの予想通り上方向（y軸と反対の向き）の力が発生して、猫が上方向に運動するね♪

はやぶさ

正解！じゃあ猫が天井より上にいるときは？

猫が天井よりも上にいるとき

同じように考えてみます。

【猫が天井よりも上にいるときの条件式】

Y > Yc

30 > Yc

もし猫の位置：Yc =20なら、ばね変位は以下の式で算出できます。

【猫が天井よりも下にいるときの”ばね変位”】

x ＝ Yc – Y

x ＝ 20 – 30

x ＝ -10

先ほど求めたバンジーの運動方程式に代入してみます。

【バンジーの運動方程式】

F = m・g – k・x

F = 1*9.8 – 5・(-10)

F = 9.8 + 50

F = 59.8

F > 0

Fがプラスになってる！！

具体的な数値を代入することで、下方向（y軸と同じの向き）の力が発生して、猫が下方向に運動する状態を確認できた！

そして、猫の位置が天井より上でも下でも同じ運動方程式が使えることも分かった！猫の位置によって数式を変える必要はないみたい！

はやぶさ

大正解！

算出した運動方程式に対し、具体的な数値を代入することで、不自然な解になっていないか？
を確認できますよ(*･ω･)ﾉ♪

くるる

はやぶさ先生ありがとう！今回は間違えちゃったけど、はやぶさ先生のおかげで二度と間違えない気がするよ♪

どういたしまして(*’ω’*)

間違えてもOK！失敗しても大丈夫！！重要なのは、その後の行動です。勇気を出して自分の失敗を告白してくれた”くるる”ちゃんに拍手♪おかげで丁寧な解説ができました

最終的に完成したソースコード -バンジージャンプ猫-

以上より、最終的に完成した「バンジージャンプ猫」のソースコードが以下です。

import pyxel

# ====== Image parameters ======
WINDOW_H = 120
WINDOW_W = 160
CAT_H = 16
CAT_W = 16

# ===== Physical parameters =====
FPS = 30     # フレームレート [f/s]
DT = 1 / FPS # ステップ時間 [s]
G = 9.8      # 重力加速度 [kg.m/s^2]
K = 5        # ばね定数 [n/m]

class Vec2:
    def __init__(self, x, y):
        self.x = x
        self.y = y

class cat:
    def __init__(self, img_id):
        self.pos = Vec2(0, 0)
        self.vec = 0
        self.vel = 0
        self.weight = 1
        self.time = 0
        self.img_cat = img_id

    def update(self, x, y, dx):
        self.pos.x = x
        self.pos.y = y
        self.vec = dx

class Ceiling:
    def __init__(self):
        self.pos1 = Vec2(0, 30)
        self.pos2 = Vec2(WINDOW_W, 35)
        self.color = 12 # blue

class Spring:
    def __init__(self):
        self.pos1 = Vec2(0, 0)
        self.pos2 = Vec2(0, 0)
        self.color = 12 # blue

    def update(self, x1, y1, x2, y2, color):
        self.pos1.x = x1
        self.pos1.y = y1
        self.pos2.x = x2
        self.pos2.y = y2
        self.color = color

class App:
    def __init__(self):
        self.IMG_ID0_X = 60
        self.IMG_ID0_Y = 65
        self.IMG_ID0 = 0
        self.IMG_ID1 = 1
        # self.IMG_ID2 = 2

        pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel")
        pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png")
        pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png")

        pyxel.mouse(True)

        # make instance
        self.Cats = []
        self.Springs = []
        self.ceiling = Ceiling()

        pyxel.run(self.update, self.draw)

    def update(self):
        if pyxel.btnp(pyxel.KEY_Q):
            pyxel.quit()

        # ====== ctrl cat ======
        if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON):
            new_cat = cat(self.IMG_ID1)
            new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec)
            self.Cats.append(new_cat)

            new_spring = Spring()
            self.Springs.append(new_spring)

        cat_count = len(self.Cats)
        for i in range(cat_count):
            if self.Cats[i].pos.y < WINDOW_H:
                # ばね変位：x（猫のｙ座標 - 天井のｙ座標）
                x = self.Cats[i].pos.y - self.ceiling.pos2.y
                # f = m * g - k * x（重力 - 復元力）
                f = self.Cats[i].weight * G - K * x
                # a = f / m （ニュートンの運動方程式）
                alpha = f / self.Cats[i].weight
                # v += a * dt （積分：加速度 ⇒ 速度）
                self.Cats[i].vel += alpha * DT
                # y += v * dt (積分：速度 ⇒ 位置)
                self.Cats[i].pos.y += self.Cats[i].vel * DT
                # 経過時間
                self.Cats[i].time += DT

                # debug
                print("Cat No.", i)
                print("v = ", self.Cats[i].vel)
                print("y = ", self.Cats[i].pos.y)
                print("f = ", f)

                # Cat update
                self.Cats[i].update(self.Cats[i].pos.x, 
                                    self.Cats[i].pos.y, 
                                    self.Cats[i].vec)

                # Spring update
                self.Springs[i].update(self.Cats[i].pos.x + CAT_W / 2, 
                                        self.ceiling.pos2.y, 
                                        self.Cats[i].pos.x + CAT_W / 2, 
                                        self.Cats[i].pos.y,
                                        pyxel.frame_count % 16)

            else:
                del self.Cats[i]
                break

    def draw(self):
        pyxel.cls(0)
        pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16)
        pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16)

        # ======= draw cat ========
        for cats in self.Cats:
            pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5)

        # ======= draw springs ========
        for springs in self.Springs:
            pyxel.line(springs.pos1.x, springs.pos1.y, 
                       springs.pos2.x, springs.pos2.y, 
                       springs.color)

        # ======= draw ceiling ========
        pyxel.rect(self.ceiling.pos1.x, self.ceiling.pos1.y, 
                    self.ceiling.pos2.x, self.ceiling.pos2.y, 
                    self.ceiling.color)

App()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

import pyxel

# ====== Image parameters ======

WINDOW_H = 120

WINDOW_W = 160

CAT_H = 16

CAT_W = 16

# ===== Physical parameters =====

FPS = 30 # フレームレート [f/s]

DT = 1 / FPS # ステップ時間 [s]

G = 9.8 # 重力加速度 [kg.m/s^2]

K = 5 # ばね定数 [n/m]

class Vec2:

def __init__(self, x, y):

self.x = x

self.y = y

class cat:

def __init__(self, img_id):

self.pos = Vec2(0, 0)

self.vec = 0

self.vel = 0

self.weight = 1

self.time = 0

self.img_cat = img_id

def update(self, x, y, dx):

self.pos.x = x

self.pos.y = y

self.vec = dx

class Ceiling:

def __init__(self):

self.pos1 = Vec2(0, 30)

self.pos2 = Vec2(WINDOW_W, 35)

self.color = 12 # blue

class Spring:

def __init__(self):

self.pos1 = Vec2(0, 0)

self.pos2 = Vec2(0, 0)

self.color = 12 # blue

def update(self, x1, y1, x2, y2, color):

self.pos1.x = x1

self.pos1.y = y1

self.pos2.x = x2

self.pos2.y = y2

self.color = color

class App:

def __init__(self):

self.IMG_ID0_X = 60

self.IMG_ID0_Y = 65

self.IMG_ID0 = 0

self.IMG_ID1 = 1

# self.IMG_ID2 = 2

pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel")

pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png")

pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png")

pyxel.mouse(True)

# make instance

self.Cats = []

self.Springs = []

self.ceiling = Ceiling()

pyxel.run(self.update, self.draw)

def update(self):

if pyxel.btnp(pyxel.KEY_Q):

pyxel.quit()

# ====== ctrl cat ======

if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON):

new_cat = cat(self.IMG_ID1)

new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec)

self.Cats.append(new_cat)

new_spring = Spring()

self.Springs.append(new_spring)

cat_count = len(self.Cats)

for i in range(cat_count):

if self.Cats[i].pos.y < WINDOW_H:

# ばね変位：x（猫のｙ座標 - 天井のｙ座標）

x = self.Cats[i].pos.y - self.ceiling.pos2.y

# f = m * g - k * x（重力 - 復元力）

f = self.Cats[i].weight * G - K * x

# a = f / m （ニュートンの運動方程式）

alpha = f / self.Cats[i].weight

# v += a * dt （積分：加速度 ⇒ 速度）

self.Cats[i].vel += alpha * DT

# y += v * dt (積分：速度 ⇒ 位置)

self.Cats[i].pos.y += self.Cats[i].vel * DT

# 経過時間

self.Cats[i].time += DT

# debug

print("Cat No.", i)

print("v = ", self.Cats[i].vel)

print("y = ", self.Cats[i].pos.y)

print("f = ", f)

# Cat update

self.Cats[i].update(self.Cats[i].pos.x,

self.Cats[i].pos.y,

self.Cats[i].vec)

# Spring update

self.Springs[i].update(self.Cats[i].pos.x + CAT_W / 2,

self.ceiling.pos2.y,

self.Cats[i].pos.x + CAT_W / 2,

self.Cats[i].pos.y,

pyxel.frame_count % 16)

else:

del self.Cats[i]

break

def draw(self):

pyxel.cls(0)

pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16)

pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16)

# ======= draw cat ========

for cats in self.Cats:

pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5)

# ======= draw springs ========

for springs in self.Springs:

pyxel.line(springs.pos1.x, springs.pos1.y,

springs.pos2.x, springs.pos2.y,

springs.color)

# ======= draw ceiling ========

pyxel.rect(self.ceiling.pos1.x, self.ceiling.pos1.y,

self.ceiling.pos2.x, self.ceiling.pos2.y,

self.ceiling.color)

App()

実は本記事”Day5”のソースコードは、”Day４”記事で紹介したソースコードとほとんど同じです。

どちらも”ばね特性”（復元力）を題材にしているので、当然かもしれませんが…それでも学びがあったのではないでしょうか？

くるる

すごーーく勉強になりました

くるるちゃんは、また１つ賢くなりました♪

おわりに

『Pythonで物理シミュレーションをしよう！Day5 -復元力２-』について説明しました。

”Day４”と同じ”ばねの復元力”を題材にしたチュートリアルでしたが、簡単に違いをまとめると以下の通りです。

【Day4 -トランポリンの物理シミュレーション-】

猫とばねが非接触の状態がある
復元力が上方向にしか発生しない

【Day5 -バンジーの物理シミュレーション-】

猫とばねが常に接触状態
復元力が上下方向に発生する

くるる

同じ題材なのに、新鮮な気持ちで楽しめた！

はやぶさ

ありがとう！

pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本記事を書きあげました。

本記事をきっかけに「物理」や「プログラミング」に興味をもってくれる人が増えたら最高に嬉しいです！

くるる

くるるのおかげで、はやぶさ先生は最高に喜んでる！笑

はやぶさ

そうだね。くるるちゃんと勉強するのは最高に楽しいぞー。じゃあ、今日はいつものセリフ一緒にやるか！

くるる

駆け出しエンジニア”くるる”@kururu_owl と

はやぶさ

理系応援ブロガー”はやぶさ”@Cpp_Learningは

くるる

頑張る理系を応援します！

息ピッタリでした！笑

本シリーズ最終回？？

次回予告

『Pythonで物理シミュレーションしよう！』シリーズ記事ですが、本記事が最終回の予定でした。

ただ、”くるる”ちゃんが最終回とは別の理由で泣き出すから…

くるる

蜘蛛の糸に吊るされたスパイダーマンは静止した状態で街を見下ろすのに！！

くるる

バンジーの物理シミュレーションは最高に楽しかったけど、全然静止しない！あれじゃ”びよんびよん”してる猫じゃん！！

はやぶさ

えーと…最初から”びよんびよん”してる猫のつもりで…

くるる

それに猫ちゃんがいつまでも静止しないのは可哀想！！

”くるる”ちゃんのピュア想いが私の心に突き刺さった…！

”くるる”ちゃん！顔を上げて！猫が静止するよ！

くるる

スパイダーマンきたーーーー！！

嬉しさのあまり踊りだす、”くるる”ちゃんがすごく可愛い♪

というわけで、次回が本シリーズの最終回になります。

”Day4”では、思わせぶりな記事を書いてしまい申し訳ありませんでした。本シリーズは良くも悪くも無計画で作成しているため、今回のようなハプニングが発生しました！笑

くるる

楽しみが増えてラッキー♪

”くるる”ちゃんと同じ思いの人がいたら嬉しいです。

本記事楽しかったかな？次回もお楽しみに～

【Pyxel】Pythonで物理シミュレーションをしよう！ Day 3 -反発-こんにちは！前回こんな記事を書きました↓ https://cpp-learning.com/pyxel_p...

【Pyxel】Pythonで物理シミュレーションをしよう！ Day 4 -復元力-こんにちは！前回こんな記事を書きました↓ https://cpp-learning.com/pyxel_p...

【Pyxel】Pythonでレトロゲームを作ろう！総集編 -まるっと1週間でゲーム開発入門-Python向けのレトロゲームエンジン：pyxelを用いたゲーム開発入門チュートリアル（ソースコード付き）を書きました。画像処理・数学・物理・制御について学び、実践としてゲームプログラミングまで行います。...

【Python】ゲームソフト開発を題材にしたオブジェクト指向入門ゲームソフト作成を題材にした「オブジェクト指向」の入門記事を書きました。オブジェクト図/クラス図の書き方や考え方のポイントも説明した実践的な内容になっています！ソフトウェア設計やソフトウェア開発を学びたい人にオススメの記事です！...

【Processing入門】画像処理プログラミングでプロモーションビデオ作成教育用途やデジタルアートなど様々な用途があるプログラミング言語Processingの入門チュートリアルを作りました。オリジナル動画を作るためのサンプルコードも公開しています。...

【ソフトウェア開発入門チュートリアル】OpenCVとPythonで『物体追跡カメラ』を作るソフトウェア開発入門のチュートリアル記事を書きました。本記事では、OpenCVとPythonを使った『物体追跡カメラ』の開発を題材に、開発プロセス・設計・実装（コーディング）などのソフトウェア開発に関する知識を一通り学べる内容になっています。...

【Pyxel】Pythonで物理シミュレーションをしよう！ Day 5 -復元力２-

前回までに学んだこと

【Day5】Pyxelで物理シミュレーション

バンジーの物理シミュレーション

【復習】トランポリンと復元力

バンジーロープと復元力

くるるの失敗！？

猫が天井よりも下にいるとき

猫が天井よりも上にいるとき

最終的に完成したソースコード -バンジージャンプ猫-

おわりに

次回予告

プライム感謝祭セールを完全攻略！事前準備やお得キャンペーンを徹底解説

【アマゾンプライムデー2023年】完全攻略！事前準備やお得キャンペーンを徹底解説

【2023年版】アマゾンプライム会員のメリット・デメリットを紹介！

Golang × WebAssembly（wasm）入門

【Python】最適化フレームワークのCodable Model Optimizerで回帰モデルのパラメータ調整を自動化する

【GitHub】シンプルなREADME.mdの書き方 -コピペで使えるテンプレート付き-

【Pyxel】Pythonでレトロゲームを作ろう！総集編 -まるっと1週間でゲーム開発入門-

【仕事効率化】Visual Studio Code で Markdown を使いこなす

【深層学習入門】画像処理の基礎(画素操作)からCNN設計まで

【Pyxel】Pythonでレトロゲームを作ろう！ Day 1 -画像の扱い方-

前回までに学んだこと

【Day5】Pyxelで物理シミュレーション

バンジーの物理シミュレーション

【復習】トランポリンと復元力

バンジーロープと復元力

くるるの失敗！？

猫が天井よりも下にいるとき

猫が天井よりも上にいるとき

最終的に完成したソースコード -バンジージャンプ猫-

おわりに

次回予告

プライム感謝祭セールを完全攻略！事前準備やお得キャンペーンを徹底解説

【アマゾンプライムデー2023年】完全攻略！事前準備やお得キャンペーンを徹底解説

【2023年版】アマゾンプライム会員のメリット・デメリットを紹介！

Golang × WebAssembly（wasm）入門

【Python】最適化フレームワークのCodable Model Optimizerで回帰モデルのパラメータ調整を自動化する

【GitHub】シンプルなREADME.mdの書き方 -コピペで使えるテンプレート付き-

【Pyxel】Pythonでレトロゲームを作ろう！ 総集編 -まるっと1週間でゲーム開発入門-

【仕事効率化】Visual Studio Code で Markdown を使いこなす

【深層学習入門】画像処理の基礎(画素操作)からCNN設計まで

【Pyxel】Pythonでレトロゲームを作ろう！ Day 1 -画像の扱い方-

【Pyxel】Pythonでレトロゲームを作ろう！総集編 -まるっと1週間でゲーム開発入門-