こんにちは！
前回こんな記事を書きました↓
本記事は『Pythonで物理シミュレーションをしよう！』シリーズの”Day6”です！
くるるちゃんの言う通り、約1か月続いた『Pythonで物理シミュレーションをしよう！』シリーズは本記事で最終回です。
Contents
前回までに学んだこと
”Day５”の記事では「バンジージャンプする猫」の物理シミュレーションを実践しました。
今回も「バンジージャンプする猫」ですが、猫の移動量が減衰し、最終的に猫が静止する物理シミュレーションになっています。
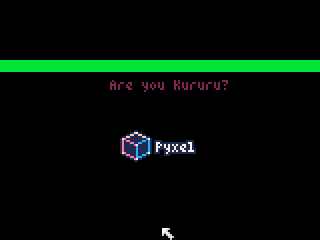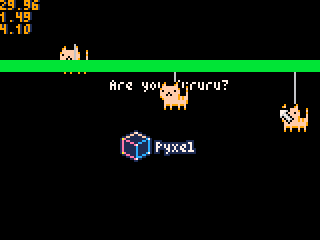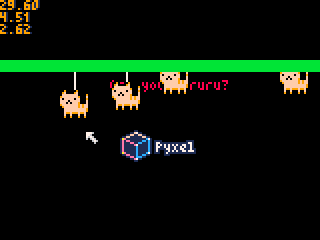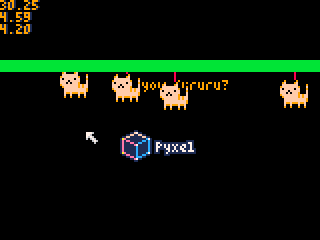
猫を心配する”くるる”ちゃんが今日も可愛い(*･ω･)ﾉ♪
【Day6】Pyxelで物理シミュレーション
くるるちゃん鋭い！色んな勉強方法がありますが、プログラミング/データサイエンス/シミュレーションなどトライ＆エラーを実践しやすいものは、以下の勉強方法が良いと考えています。
- 仮説を立てる（こうじゃないか？という自分の考えをもつ）
- 立証する（実践じゃーーー！）
【復習】バンジーロープと復元力（知識の整理）
くるるちゃんの仮説「速度に応じて移動量を減衰させる力が働いた」を立証する前に、知識を整理します。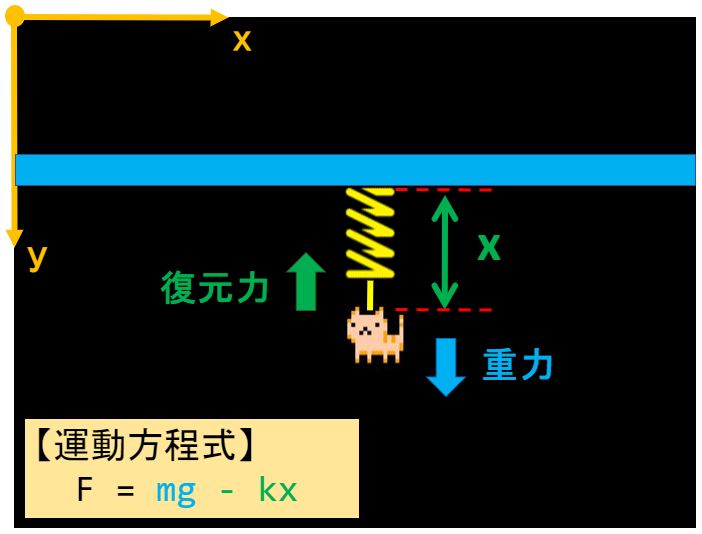
猫が静止しない”Day５”バンジーの運動方程式は以下の通りでした。
【重力の運動方程式】
f1 = m・g (質量：m[kg], 重力加速度g[m/s^2])
【復元力の運動方程式】
f2 = k・x (ばね定数：k[N/m], 変位x[m])
【バンジーの運動方程式】
F = f1 – f2
F = m・g – k・x
※y軸の向きに注意
知識を整理することが課題解決の近道になることがあります。定期的に自分の知識や技術を整理し、後戻りの少ないアプローチで課題を解決したいですね。
以下２点を検討し、知識を整理することが課題解決の近道になるときがあります
- 自分がどんな知識や技術を習得しているか？
- 目の前の課題や問題は、習得済みの知識や技術で解決できなか？
【仮説】バンジーロープと減衰力
続いて”くるる”ちゃんの仮説「速度に応じて移動量を減衰させる力が働いた」を図で表現します。
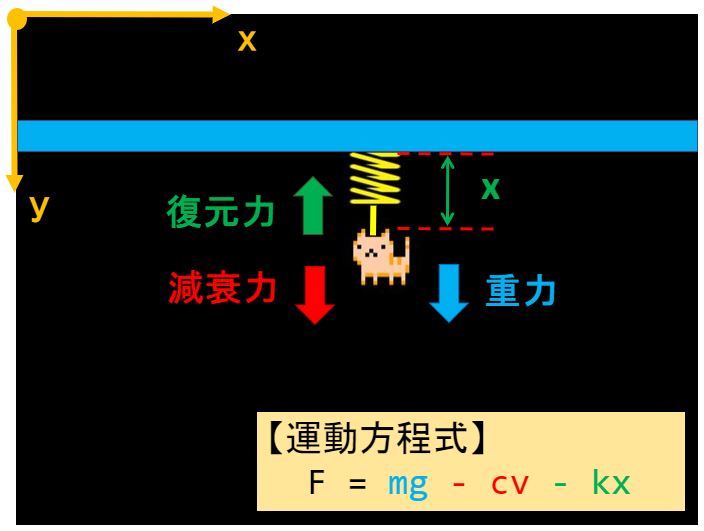
速度に応じて力が発生し、かつ移動量を減衰させる方向に働く”減衰力”を追記しました。
これを数式に落とし込みます。
【重力の運動方程式】
f1 = m・g (質量：m[kg], 重力加速度g[m/s^2])
【復元力の運動方程式】
f2 = k・x (ばね定数：k[N/m], 変位x[m])
【減衰力の運動方程式】
f3 = c・v (減衰系数：c[N/m/s], 速度v[m/s])
【バンジーの運動方程式】
F = f1 – f3 – f2
F = m・g – c・v – k・x
※y軸の向きに注意
くるるちゃんは理解できているようですが、念のため説明します。
猫が天井よりも下にいるときは、ばねの復元力で猫が上方向（y軸と反対の向き）に移動します。
つまり、猫の移動速度は負になります。具体的な数値”v = -2”を代入して、力の方向を確認します。
【減衰力の運動方程式】
f3 = c・v
f3 = c・(-2)
【バンジーの運動方程式】
F =f1 – f3 – f2
F =m・g – c・(-2) – k・x
F =m・g + 2・c – k・x
重力と減衰力が正（下方向）、復元力が負（上方向）になることを確認できました(*･ω･)ﾉ♪
最後はソースコードに落とし込みます。
|
1 2 3 4 5 6 7 8 |
# ばね変位：x（猫のｙ座標 - 天井） x = self.Cats[i].pos.y - self.ceiling.pos2.y ''' # f = m * g - k * x（重力 - 復元力） f = self.Cats[i].weight * G - K * x ''' # f = m * g - k * x（重力 - 減衰力 - 復元力） f = self.Cats[i].weight * G - C * self.Cats[i].vel - K * x |
コメントアウトしているコードは”Day５”の運動方程式です。ベースが同じ運動方程式に減衰力を追加するだけで、別のシミュレーションになることを理解してほしいので、あえて消さずに残しておきました
最終的に完成したソースコード -バンジー猫(減衰あり)-
最後はソースコードを作成して物理シミュレーションを実践じゃーーー！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 |
import pyxel # ====== Image parameters ====== WINDOW_H = 120 WINDOW_W = 160 CAT_H = 16 CAT_W = 16 # ===== Physical parameters ===== FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] K = 5 # ばね定数 [n/m] C = 0.4 # 減衰係数 [n/v] class Vec2: def __init__(self, x, y): self.x = x self.y = y class cat: def __init__(self, img_id): self.pos = Vec2(0, 0) self.vec = 0 self.vel = 0 self.weight = 1 self.time = 0 self.img_cat = img_id def update(self, x, y, dx): self.pos.x = x self.pos.y = y self.vec = dx class Ceiling: def __init__(self): self.pos1 = Vec2(0, 30) self.pos2 = Vec2(WINDOW_W, 35) self.color = 11 # green class Spring: def __init__(self): self.pos1 = Vec2(0, 0) self.pos2 = Vec2(0, 0) self.color = 12 # blue def update(self, x1, y1, x2, y2, color): self.pos1.x = x1 self.pos1.y = y1 self.pos2.x = x2 self.pos2.y = y2 self.color = color class App: def __init__(self): self.IMG_ID0_X = 60 self.IMG_ID0_Y = 65 self.IMG_ID0 = 0 self.IMG_ID1 = 1 # self.IMG_ID2 = 2 pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel") pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png") pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png") pyxel.mouse(True) # make instance self.Cats = [] self.Springs = [] self.ceiling = Ceiling() pyxel.run(self.update, self.draw) def update(self): if pyxel.btnp(pyxel.KEY_Q): pyxel.quit() # ====== ctrl cat ====== if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON): new_cat = cat(self.IMG_ID1) new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec) self.Cats.append(new_cat) new_spring = Spring() self.Springs.append(new_spring) cat_count = len(self.Cats) for i in range(cat_count): if self.Cats[i].pos.y < WINDOW_H: # ばね変位：x（猫のｙ座標 - 天井） x = self.Cats[i].pos.y - self.ceiling.pos2.y ''' # f = m * g - k * x（重力 - 復元力） f = self.Cats[i].weight * G - K * x ''' # f = m * g - k * x（重力 - 減衰力 - 復元力） f = self.Cats[i].weight * G - C * self.Cats[i].vel - K * x # a = f / m （ニュートンの運動方程式） alpha = f / self.Cats[i].weight # v += a * dt （積分：加速度 ⇒ 速度） self.Cats[i].vel += alpha * DT # y += v * dt (積分：速度 ⇒ 位置) self.Cats[i].pos.y += self.Cats[i].vel * DT # 経過時間 self.Cats[i].time += DT # debug print("Cat No.", i) print("v = ", self.Cats[i].vel) print("y = ", self.Cats[i].pos.y) print("f = ", f) # Cat update self.Cats[i].update(self.Cats[i].pos.x, self.Cats[i].pos.y, self.Cats[i].vec) # Spring update self.Springs[i].update(self.Cats[i].pos.x + CAT_W / 2, self.ceiling.pos2.y, self.Cats[i].pos.x + CAT_W / 2, self.Cats[i].pos.y, pyxel.frame_count % 16) else: del self.Cats[i] break def draw(self): pyxel.cls(0) pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16) pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16) # ======= draw cat ======== for cats in self.Cats: pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5) # ======= draw springs ======== for springs in self.Springs: pyxel.line(springs.pos1.x, springs.pos1.y, springs.pos2.x, springs.pos2.y, springs.color) # ======= draw ceiling ======== pyxel.rect(self.ceiling.pos1.x, self.ceiling.pos1.y, self.ceiling.pos2.x, self.ceiling.pos2.y, self.ceiling.color) App() |
意図した動き…今回の場合は猫の移動量が減衰し、最終的に静止する物理シミュレーションを実現できれば、仮説を立証できたことになります。
減衰力とは
今回くるるちゃんが閃いた「速度に応じて移動量を減衰させる力」というのは「減衰力」と呼ばれている力で、教科書にも載っている一般的によく知られた物理現象です。
”Day４”記事のサブタイトル「復元力」については、ばねを例に説明しました。
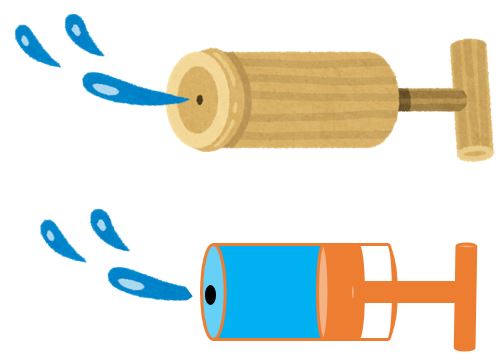
本記事のサブタイトル「減衰力」については、竹筒の底に穴を空けたタイプの水鉄砲を例に説明します。（この例が伝わらなかったらジェネレーションギャップを感じてしまう…）
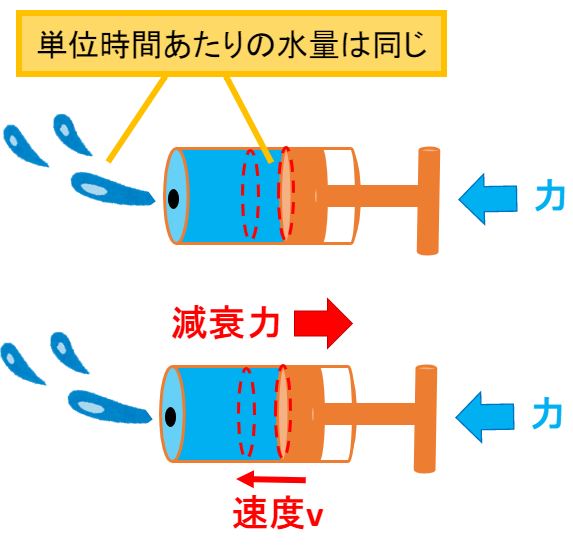上図の通り、「穴から出ていく水量（体積）」と「力を加えて押された水量（赤破線の体積）」は同じになります。
より正確には「単位時間当たりの水量が同じ」になります。
もし、多くの水を出すために、強い力を加えたとしても、穴の大きさは常に同じなので、出ていく水量は変わりません。
むしろ、ピストンを素早く動かして赤破線の体積を大きくしようとすればするほど「減衰力」が大きくなります。
これを数式で表現すると速度に比例して「減衰力」が大きくなる以下の式になります。
【減衰力の運動方程式】
f = c・v (減衰系数：c[N/m/s], 速度v[m/s])
バンジーの運動方程式で説明済みの式ですね。
この水鉄砲と同じ原理で減衰力を発生させ、新幹線や建物の振動を減衰させる「ダンパー」という装置があります。
ただし、今回のバンジーロープのようにダンパーが存在しなくても、「空気抵抗」や「材料特性」・「（建物などの）構造」により、振動していた物体は自然に減衰する場合がほとんどです。
ダンパーの有無や各種の影響により、減衰係数の大きさは異なりますが、振動が減衰するときに発生している減衰力は、上の式で表現できる場合が多いです。
いつもは冒頭で説明している理論の説明を本記事では終盤にしました。その意図とは…？本記事の【あとがき】で説明しますね。
おわりに
『Pythonで物理シミュレーションをしよう！Day6 -減衰力-』について説明しました。
pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本シリーズを書きあげました。
約一週間（6日間）で完結し、Step by Stepでレベルアップできるチュートリアルに仕上げました（全記事ソースコード付）
くるるちゃんのように楽しく勉強してくれた人がいたら、とても嬉しいです！そして、もっと勉強したい！という人がいたら最高に嬉しいです！！
『Pythonで物理シミュレーションをしよう！ 』シリーズ（完）
次回予告がないので、【あとがき】を書きました。時間がある人は以下も読んでみてね。
【あとがき】本シリーズの最終回に込めた想い
チュートリアルというのは、以下のストーリで説明する場合が多いです。
【チュートリアルのストーリー展開】
- 概要説明
- 理論説明
- 実践（シミュレーション）
本シリーズ記事も例外ではなく、”Day１”～”Day５”までは上記のストーリーで説明しました。
しかし、最終回の本記事は以下のストーリで説明しました。
【最終回（本記事）のストーリー展開】
- 未知の現象に対し、仮説をたてる
- 物理シミュレーションを実践して仮説を立証
- 理論説明
これは”答え”の分からない課題を解く場合のアプローチと同じです。
教科書や論文で得た知識を”そのまま”課題解決に活かせる場合もありますが、現時点で習得していない知識が必要な課題（壁）にぶつかるときがあります。
その場合、以下のことを検討するのが課題解決の近道になるかもしれません。
- 現時点で習得している知識で課題を解決できないか？
- どんな知識や技術を新規に習得すれば、課題を解決できるか？
ジグソーパズルで例えると以下の通りです。
- 手持ちの要素技術ピースで解決できるか？
- 欠けているピースは何か？
”欠けているピース”を「リサーチして見つける」か「独自の数式モデルやアルゴリズムを作成する」かはケースバイケースですが…
物理の勉強を始めたばかりの”くるる”ちゃんは「減衰力」というピースを持っていませんでした。しかし、「速度に応じて移動量を減衰させる力が働いた」という仮説を立て、”欠けているピース”としました。
あとは、”欠けているピース”を図や数式で表現した後、最終的にはソースコードを作成し、物理シミュレーションを実践することで、仮説を立証しました。
つまり、”欠けているピース”を自分の”手持ちのピース”に加えることに成功しました。
今後、くるるちゃんが本シリーズで紹介していない物理シミュレーションに挑戦するとき、今度は「手持ちの減衰力ピース」を用いて、簡単に実践できるかもしれませんね♪
本シリーズをきっかけに「物理」や「プログラミング」に興味をもってくれた人が、新しい何かに挑戦したいと思ったとき…本記事のアプローチが参考になるかもしれません。
本記事を読んでくれた全ての人が、自力で課題を解決できる（自走できる）人になってほしいと願っています。
自分のペースで「要素技術のピース」を増やしていき、あらゆる課題を解決できる人に成長して下さいね。
以上 某企業の研究所に勤務する現役エンジニア兼メンターからのメッセージでした。
（完）
