こんにちは！
前回こんな記事を書きました↓
本記事は『Pythonで物理シミュレーションをしよう！』シリーズの”Day3”です！
Contents
前回までに学んだこと
”Day２”の記事では「地面に綺麗に着地する猫」の物理シミュレーションを実践しました。
本記事では「地面に反発する猫」の物理シミュレーションを実践します。
なお、本記事の内容は”Day２”の記事で学んだ内容がベースになるため、まだ”Day２”の記事を読んでいない人や内容を忘れてしまった人は先に読んで頂けると嬉しいです。
勉強熱心な”くるる”ちゃんが今日も可愛い(*･ω･)ﾉ♪
以下の記事を先に読めば、本記事の内容をスムーズに理解できます。
【Day3】Pyxelで物理シミュレーション
Day2の内容を簡単に復習した後、「地面に反発する猫」の物理シミュレーションについて説明していきます。
最近、3歳になった”くるる”ちゃんがカッコイイ！
Day2の復習
”Day２”の記事を読んでくれた人は【復習】を飛ばしてOKだよー
【復習】猫と地面の当たり判定
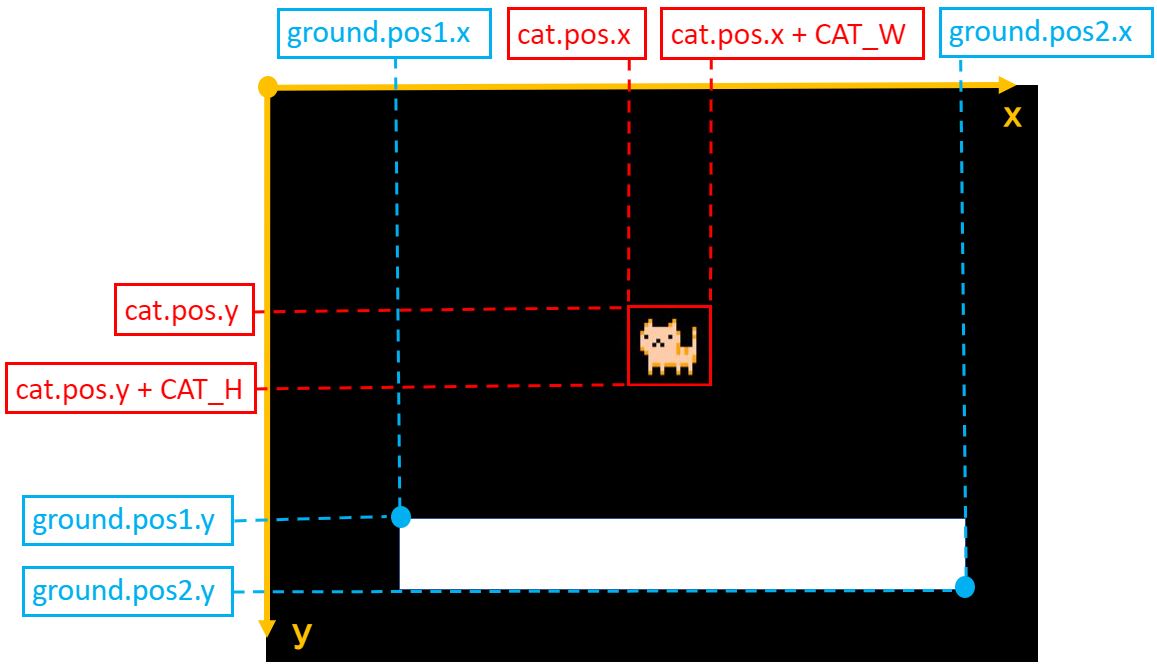猫と地面の座標が↑の通りでした。
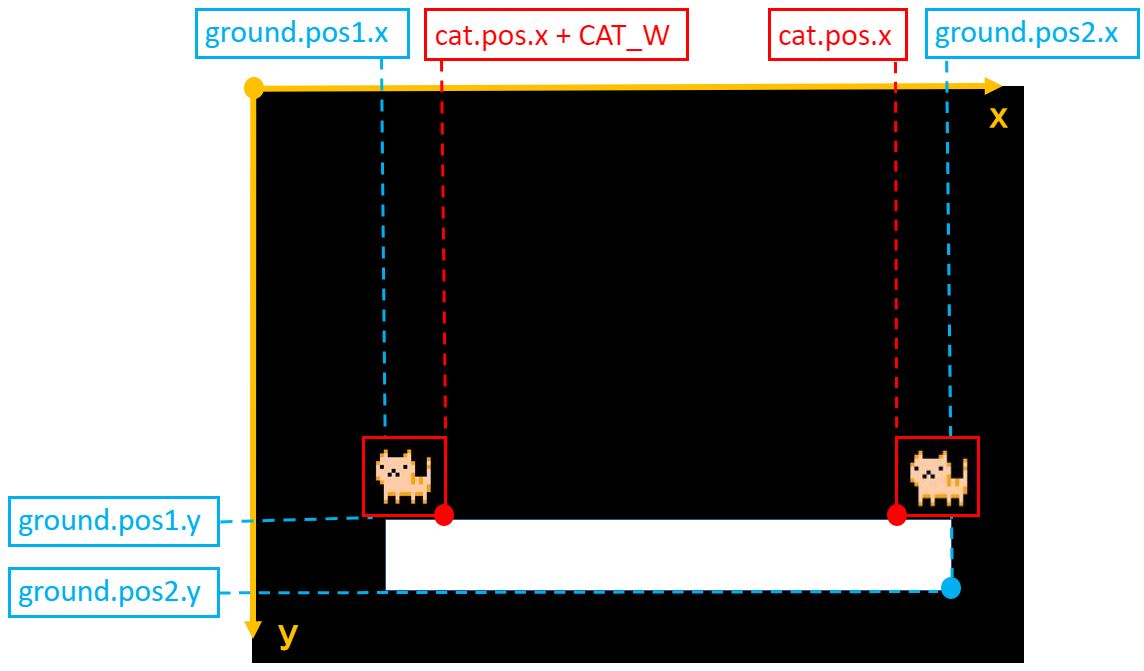
また、「猫が落下する」＝「猫が地面に当たっていない」という状態でした。
”Day２”記事のポイントは…
でした。条件式については以下の通りだよー
【猫が着地】
猫の足が地面に接触あるいは地面に足が埋まる状態
かつ
猫が地面の内側にいる状態
これを数式に落とし込むと…
【猫が着地】
ground.pos1.y <= self.Cats[i].pos.y + CAT_H
かつ
ground.pos1.x <= Cats[i].pos.x + CAT_W
かつ
Cats[i].pos.x <= ground.pos2.x
最後にソースコードで表現すると以下の通りです。
|
1 2 3 4 |
if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): # 地面に当たったときの処理（着地したときの処理） |
【復習】物理シミュレーション -地面に綺麗に着地-
「猫が地面に綺麗に着地した」というのが、どんな現象（どんな状態）なのか？を考えるんだったよね？覚えてるかな？
”Day２”記事では、以下のように考えたよね♪
- 猫が綺麗に着地する
- 地面に当たって静止状態になる
- 地面に当たったとき、猫の落下速度=０になる
つまり、「猫が地面に当たった」という条件（当たり判定）が”正”のとき「猫の落下速度=０」にすればOKでした。
それをソースコードで表現すると以下の通り！
|
1 2 3 4 5 |
# 地面に衝突 (綺麗に着地：速度 = ０) if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): self.Cats[i].vel = 0 |
学んだことを自分なりに消化吸収して、自分の言葉で説明できれば、知識が定着した証拠になります。もし機会があれば、学んだ内容を人に説明して、理解度を確認してみましょう。
以上までの内容が”Day２”記事の復習でした。
物理シミュレーション -反発-
”Day２”記事と同様に、「地面に反発する猫」というのが、どんな現象（どんな状態）なのか？を考えてみます。
これも「猫が地面に当たっていない」=「自由落下」なので「猫が地面に当たった」ときの条件式は”Day２”と同じソースコードが使えます。
つまり、「地面に当たったとき」の処理だけ考えれば良いので…
『猫が地面に当たって”反発”する』という現象を考え、数式に落とし込んでみよー♪
過去に開発したソフトウェアやネット上で公開しているソースコードを参考にして、効率良く作業できると良いですね
反発とは
「スーパーボールが地面に跳ね返る現象」が今回再現した現象に近い現象だと気が付いたよー
ある高さから落としたスーパーボールが10m/secで地面に当たり、8m/secの速度で跳ね返る…
それを繰り返すと、だんだん速度が減少していき、最後は地面の上で静止する。
この現象を物理シミュレーションで再現してみる。
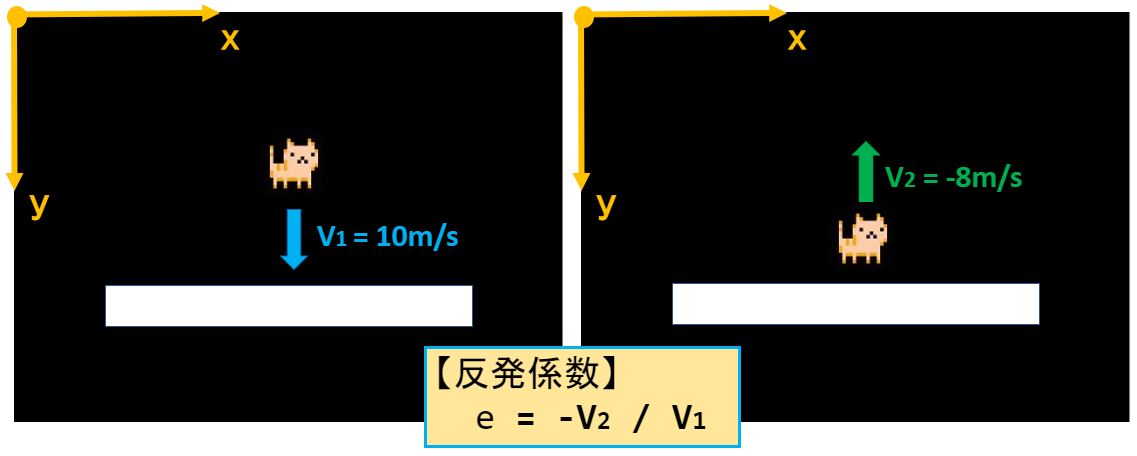
速度10m/secが8m/secになるということは…
e = 8 / 10
つまり、0.8倍の速度で跳ね返っていることになる！
y軸が下向きだから、上向きの跳ね返る速度はマイナスだ！
つまり、以下の式が正解だね(*･ω･)ﾉ♪
e = – (-8) / 10
【反発係数】
e = – V2 / V1
なるほど！！今回は速度10m/sで地面に衝突してる例を使ったけど、速度が9m/sや8m/sも考えられるもんね。
記号を使えば、代入できる全ての数値を網羅した式として表現できるね！
”くるる”ちゃんは自力で【反発係数】の式を導きました！
具体的な数値から現象を再現する数式を求められるとGoodです！そして、最終的に数式を記号で表現できれば、アルゴリズムあるいは公式を算出できたことになります。
反発のソースコード
|
1 2 3 4 5 |
# 地面に衝突 (反発：速度 = -e * 速度) if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): self.Cats[i].vel = -E * abs(self.Cats[i].vel) |
以上！今までの手順をメモしておくよー
ソフトウェアの作成手順には様々な方法がありますが、今回は以下のフローで作成しました。
- 再現したい現象を調査
- 再現したい現象を数式に落とし込む
- 数式を記号（一般系）で表現
- 数式をソースコードで実装
最終的に完成したソースコード -地面に反発-
最終的に完成した「猫が地面に反発する物理シミュレーション」のソースコードが以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 |
import pyxel # ====== Image parameters ====== WINDOW_H = 120 WINDOW_W = 160 CAT_H = 16 CAT_W = 16 # ===== Physical parameters ===== FPS = 30 # フレームレート [f/s] DT = 1 / FPS # ステップ時間 [s] G = 9.8 # 重力加速度 [kg.m/s^2] E = 0.8 # 反発係数 class Vec2: def __init__(self, x, y): self.x = x self.y = y class cat: def __init__(self, img_id): self.pos = Vec2(0, 0) self.vec = 0 self.vel = 0 self.weight = 1 self.time = 0 self.img_cat = img_id def update(self, x, y, dx): self.pos.x = x self.pos.y = y self.vec = dx class Ground: def __init__(self): self.pos1 = Vec2(30, WINDOW_H - 30) self.pos2 = Vec2(WINDOW_W - 30, WINDOW_H - 25) self.color = 7 # white class App: def __init__(self): self.IMG_ID0_X = 60 self.IMG_ID0_Y = 65 self.IMG_ID0 = 0 self.IMG_ID1 = 1 # self.IMG_ID2 = 2 pyxel.init(WINDOW_W, WINDOW_H, fps = FPS, caption="Hello Pyxel") pyxel.image(self.IMG_ID0).load(0, 0, "assets/pyxel_logo_38x16.png") pyxel.image(self.IMG_ID1).load(0, 0, "assets/cat_16x16.png") pyxel.mouse(True) # make instance self.Cats = [] self.ground = Ground() pyxel.run(self.update, self.draw) def update(self): if pyxel.btnp(pyxel.KEY_Q): pyxel.quit() # ====== ctrl cat ====== if pyxel.btnp(pyxel.MOUSE_LEFT_BUTTON): new_cat = cat(self.IMG_ID1) new_cat.update(pyxel.mouse_x, pyxel.mouse_y, new_cat.vec) self.Cats.append(new_cat) cat_count = len(self.Cats) for i in range(cat_count): if self.Cats[i].pos.y < WINDOW_H: # f = m * g （力） f = self.Cats[i].weight * G # a = f / m （ニュートンの運動方程式） alpha = f / self.Cats[i].weight # v += a * dt （積分：加速度 ⇒ 速度） self.Cats[i].vel += alpha * DT # 地面に衝突 (反発：速度 = -e * 速度) if ((self.ground.pos1.y <= self.Cats[i].pos.y + CAT_H) and(self.ground.pos1.x <= self.Cats[i].pos.x + CAT_W) and (self.Cats[i].pos.x <= self.ground.pos2.x)): self.Cats[i].vel = -E * abs(self.Cats[i].vel) # y += v * dt (積分：速度 ⇒ 位置) self.Cats[i].pos.y += self.Cats[i].vel * DT # 経過時間 self.Cats[i].time += DT # debug print("Cat No.", i) print("v = ", self.Cats[i].vel) print("y = ", self.Cats[i].pos.y) # Cat update self.Cats[i].update(self.Cats[i].pos.x, self.Cats[i].pos.y, self.Cats[i].vec) else: del self.Cats[i] break def draw(self): pyxel.cls(0) pyxel.text(55, 40, "Are you Kururu?", pyxel.frame_count % 16) pyxel.blt(self.IMG_ID0_X, self.IMG_ID0_Y, self.IMG_ID0, 0, 0, 38, 16) # ======= draw cat ======== for cats in self.Cats: pyxel.blt(cats.pos.x, cats.pos.y, cats.img_cat, 0, 0, CAT_W, CAT_H, 5) # ======= draw ground ======== pyxel.rect(self.ground.pos1.x, self.ground.pos1.y, self.ground.pos2.x, self.ground.pos2.y, self.ground.color) App() |
”Day２”記事で作成したソースコード同様、画像上の任意の位置でマウス左クリックすると猫が自由落下した後、地面に反発する物理シミュレーションを楽しめます(*･ω･)ﾉ♪
大変よくできました♪
おわりに
『Pythonで物理シミュレーションをしよう！Day3 -反発-』について説明しました。
pyxelを使って、楽しく「物理」や「プログラミング」の勉強ができると良いなーとか考えながら、本記事を書きあげました。
本記事をきっかけに「物理」や「プログラミング」に興味をもってくれた人が…
など、勉強のモチベーションが上がってくれたら、とても嬉しいです！
次回予告
『Pythonで物理シミュレーションしよう！』シリーズ記事ですが、何記事書くかなどを考えずに作成しています。
ただ、キリの良く”Day5”まで（約1週間で完結するチュートリアルとして）書き上げたいと考えています。
フクロウの大きな瞳で見つめられるとプレッシャーがスゴイ！笑
じゃあ、”くるる”ちゃんのリクエストに応えよう！
”Day4”では『地面をトランポリンにしたときの物理シミュレーション』を実践しよう！
私も勉強熱心な”くるる”ちゃんが大好きです。
次回もお楽しみに～
