こんにちは。
ディープラーニングお兄さんの”はやぶさ”@Cpp_Learningだよー
本サイトで機械学習の記事を書いてます。ただし、まだチュートリアル記事が書けてない…
書きたいけど、優秀なチュートリアル記事を公開している人は大勢いるし、自分が書かなくても良いかぁ…と思いながら独り言のように以下のツイートをしたら…
私も機械学習のチュートリアル記事書きたいけど、ライバル多そうだな。。 https://t.co/KspmZAJA0v
— はやぶさ (@Cpp_Learning) July 28, 2018
「読みたーい」と言ってくれる人がいました。
ディープラーニングお兄さんは、人から期待されたり、頼りにされると人一倍頑張れるのです！
「書きまーす」と回答して、さっそく執筆に取り掛かりました。
記事を書き進めながら、やっぱり他の人と同じことをしてもしょうがないよなぁと思い、深層学習の入門レベルだけどで、超実践的な内容に仕上げようと考えました。
そこで、本記事では『深層学習でシステム解析する方法』を説明したいと思います。
本記事をきっかけに、深層学習をもっと学びたい！という人が増えると嬉しい(*･ω･)ﾉ♪
説明とか少しでイイから、ソースコード見せて！という人は目次から『はやぶさの技術ノート』にジャンプして下さい。
Contents
本記事をオススメしたい人
先に”種明かし”すると以降から『深層学習で非線形回帰モデルを生成する方法』を説明します。
なんだ非線形回帰か…もう知っているよ。。という人は申し訳ありません。さらに高いレベルを目指して下さい。
本記事は、主に以下の人に読んでもらいたいなぁと思って書きました。
- 深層学習をビジネスや研究で使いたい
- 深層学習で何ができるか知りたい
- 深層学習のチュートリアル(MNIST等)はやったけど、その先が続かない
など、「深層学習で何かをしたい」という人に読んでもらいたいと考えています。
また、冒頭で述べた通り、レベル的には入門レベルです。
なので、具体的にやりたいことが決まってない人でも、「実践的な内容で深層学習の”使い方”を学びたい」という人にも読んでほしいと思います。ただし、以下の注意点があります。
本記事では、深層学習のアルゴリズムに関する説明はしません。あくまで、「深層学習の使い方」を中心に説明します。深層学習そのものを学びたい人には以下の本を紹介しておきます。
深層学習は手段か？目的か？
私は、企業のR＆Dに所属しており、深層学習をどう扱うべきかで日々悩んでいます。
- ”R”の立場なら「トレンドである深層学習そのものを研究すべき！」
- ”D”の立場だと「既知の課題を解決するのに深層学習を使いたい！」
となります。立場の違いで考えは変わります。色んな考えがあって良いと思いますが、私の考えは”D”よりです↓
機械学習がビジネスで使える/使えないの話しをするとき、機械学習そのものに着目しがちだが、手段と目的が逆かなーと思う
ある課題に対し機械学習で解決したい！って考えるのが⭕️
つまり
・機械学習のみ ❌
・機械学習 × 〇〇 ⭕️この〇〇に画像処理・制御・スポーツ等が入ると面白いかと↓ https://t.co/i9p8fSAufv
— はやぶさ (@Cpp_Learning) July 29, 2018
（↑ ×って書くと否定的に見えちゃうね…文字数制限を言い訳にしますが、多様な考えを否定するつもりはありません。。不快な思いをした人いたら、ごめんなさい）
深層学習そのものが面白いので、プライベートで勉強していますが、メインは「深層学習を課題解決に使いたい」という考えです。
そのため、以降から「深層学習で課題を解決する１つの例」を示しながら、深層学習の使い方を説明したいと思います。
深層学習とシステム解析
深層学習は汎用的な技術なので、あらゆる課題を解決する可能性を秘めています。
大学で制御設計に関する論文を書いた、元制御屋”はやぶさ”の立場で考えたとき、真っ先に『深層学習でシステム解析』できそうじゃん！と思いました。
この”システム解析”が今回の課題です。
システム解析とは
あるシステムを制御（思い通りに動か）したいと考えたとき、”システムの特性を把握”している必要があります。
システム解析についてザックリ説明すると、”システムの特性を把握”のために、ごにょごにょすることです。
この「対象システムの特性を把握」というのは「対象システムの数式モデル（運動方程式）を算出」と同義と考えて良いよー。（←私的にはね）
「対象システムの特性把握」＝「対象システムの数式モデル（運動方程式）算出」
システム解析と制御
システム解析により、システムの特性が y = f(x) という数式モデルで表現できることが分かれば、それは入力値xに対する出力値yが既知になったということです。
具体的には、このシステムに x = 5 を入力すれば、y = f(5) の出力値が得られるということです。このように、システムの特性（入出力関係）を把握できれば、システムを制御できます。
システムの特性（入出力関係）を把握できれば、システムを制御できます。
システム解析の課題
システム解析は、システムを構成している部品を調べ、その部品の物理特性から運動方程式を導くのが基本です。
しかし、この手法には以下の問題があります。
- 構成部品を調べきれない
- 部品の組付けが特殊で物理法則が不明確
- 摩擦などの非線形成分の把握が困難
このような問題があるため、システムに適当な入力を与え、そのときの出力から実験的にシステムの特性を把握するのが有効です。
システムの数式モデル（理論式）と実測データが異なることが多いため、実験で得られた実測データを解析して入出力関係から特性を把握するのが良いです。
システム解析の課題
実践してみます。解析対象のシステムに入力値x=0~9(整数)を与えたときの出力値yを観測します。そのときの実験データが下図です。
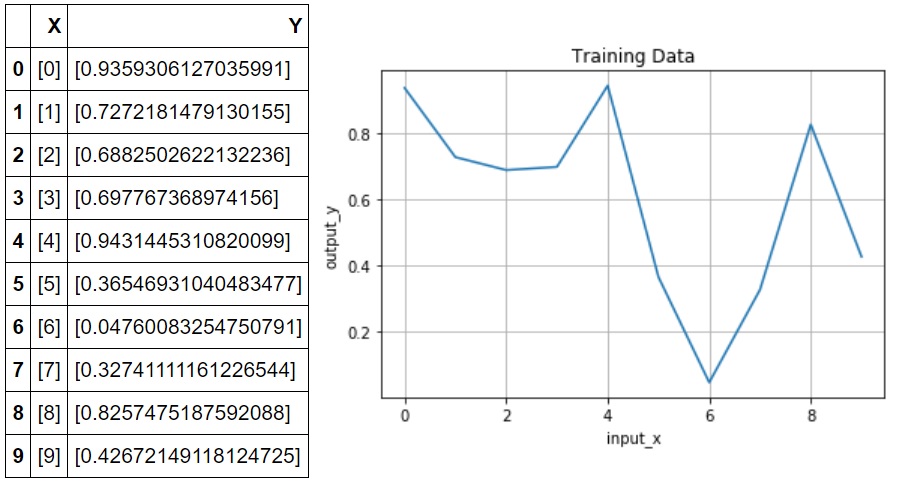
※乱数で適当な数値を生成しました。
…なにこの不規則なグラフ！非線形システムだったなんて聞いてない！！もう無理帰りたい。。となります(´；ω；｀)
冗談ではなく、このグラフの数式モデル（運動方程式）算出できます？
制御対象（解析対象）が非線形システムだと、数式モデル（特性）の算出は非常に困難です！
この課題解決に”深層学習”を使います！！
非線形システムの数式モデル算出は非常に難しい！
【超実践】Chainerと深層学習で非線形回帰モデル生成
本記事では深層学習フレームワーク”Chainer”を使って、非線形回帰モデルの生成を行いますが、重要なのは、どのフレームワークを使うかではなく、『深層学習でシステム解析が行える』という考え方です。
環境構築
本サイトでは、Chainer用の環境構築方法を２つ紹介しています。
ローカル環境でChainerを使うなら↓
オンライン実行環境でGPUを使うなら↓
まだ、環境構築が済んでいない人は、どちらか好きな方でChainer用の環境構築を実施後、手を動かしながら本記事を読み進めて頂けると理解が深まると思います。
以降から、ソースコードを交えながらシステム解析する方法を説明していきます。
import
数値演算やChainer用のモジュールなどをimportします。
|
1 2 3 4 5 6 7 8 9 10 |
import math import random import numpy as np import pandas as pd import matplotlib.pyplot as plt from chainer import Chain, Variable import chainer.functions as F import chainer.links as L from chainer import optimizers |
実験データ(ダミー)生成
本来は、解析したいシステムの入出力値をセンサ等で取得します。しかし、今回は入力値ｘ、出力値ｙの実験データ(ダミー)を生成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 実験データ用の配列 x = [] y = [] get_values = 0 for i in range(10): get_values = random.random() x.append([i]) y.append([get_values]) # データフレーム生成 df = pd.DataFrame({'X': x, 'Y': y}) # グラフ出力 plt.plot(x, y) plt.title("Training Data") plt.xlabel("input_x") plt.ylabel("output_y") plt.grid(True) df |
※解析しやすい数値で”ドヤ顔”できないように、実験データは乱数で生成しました。
このソースコードを実行すると、先ほどお見せした、以下の表と図が生成されます。
繰り返しですが、乱数を使って実験データ（ダミー）を生成しているため、このソースコードを再実行すると全く違う入出力が得られます。
Chainer用に変換
実験データx, yをChainerで使えるようにnumpy配列のfloat32に変換します。
|
1 2 |
x = Variable(np.array(x, dtype=np.float32)) y = Variable(np.array(y, dtype=np.float32)) |
ニューラルネットワーク設計
オリジナルのニューラルネットワーク『MyChain』を設計します！
ノード数が「1⇒100⇒50⇒1」となるように設計しました。100と50にした理由は…特にありません！（無理やり理由を付けるならキリの良い数字にしました。）
また、私の場合、使う活性化関数に悩んだら“relu”採用しています。（シグモイドも捨てがたい）
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
class MyChain(Chain): def __init__(self): super(MyChain, self).__init__( l1 = L.Linear(1, 100), l2 = L.Linear(100, 50), l3 = L.Linear(50, 1) ) def predict(self, x): h1 = F.relu(self.l1(x)) h2 = F.relu(self.l2(h1)) return self.l3(h2) |
これで、下図のようなノード数「1⇒100⇒50⇒1」のニューラルネットワーク『MyChain』を生成できました。
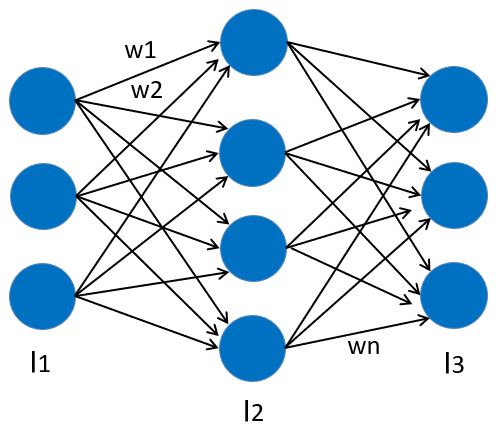（ノード数が違うとか最初と最後の”１”を省略しているとかは、目を瞑って下さい。本記事では、ニューラルネットワークの雰囲気が伝われば良いと考えています。）
急に、ニューラルネットワーク・ノード・活性化関数といった専門用語が出てきて戸惑っている人がいると思うので、簡単に説明します。
下図の青〇がノード・ノードを一列でまとめたものを層と呼びます。
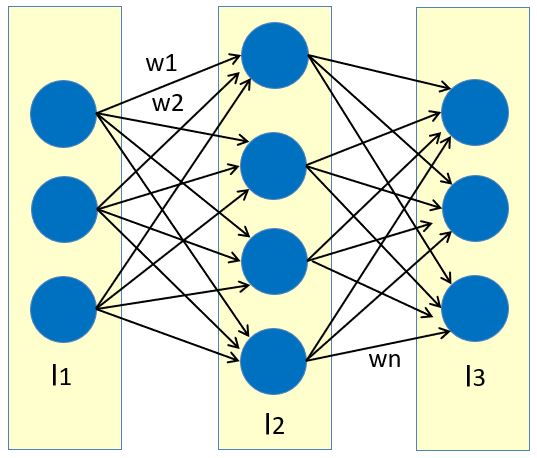
ここで知っておいてほしいのは、以下のポイントです。
- オリジナルのニューラルネットワークが数行のコードで設計できる
- l1～l3の層は増減できる
- 100・50という数値を変更すればノード数を変えられる
- 活性化関数は”relu”が良いかも
以上を踏まえ、もう一度ソースコードを見てみて下さい。
あれ？最適なネットワークの設計方法は分からないけど、少しいじるだけなら簡単にできるかも！と思ってくれると嬉しい。
本記事は、入門レベルなので「ニューラルネットワークの設計とか難しそう…」という壁を取り除ければ十分です。
本記事をきっかけに深層学習に興味を持ってもらい「最適なネットワークの設計方法を学びたい！もっと本質的なことを知りたい！」と思ってくれたら、ディープラーニングお兄さんは嬉しい！
深層学習フレームワークを使えば、比較的簡単にニューラルネットワークを設計できます。ただし、深層学習は奥が深いので、本記事をきっかけに、より良い設計方法の修得を目指してほしい！
ニューラルネットワーク（NN）モデルの宣言
↑で設計したネットワーク構造を使います！と宣言した後、いよいよ学習を行います。実は↑のネットワーク…まだ中身空っぽなんです。（生まれたてのベイビーなので）
|
1 2 |
# NNモデルの宣言 model = MyChain() |
ニューラルネットワークの設計というのは、ネットワーク構造の確定作業にすぎません。ネットワークは学習させて、はじめて課題解決のための学習済みモデルになるのです。
学習とは
深層学習という分野では、”重み”の自動調整のことを”学習”と呼びます。
先ほど設計した『MyChain』にw1・w2・wnという表記があったことに気づいてましたか？（下図参照）このw1～wnが重みです。ニューラルネットワークにはこのような重みが多数存在します。
深層学習では、”重み”の自動調整のことを”学習”と呼びます。
課題確認と深層学習
ここで改めて、今回の課題を確認しておきます。今回の課題は「深層学習でシステム解析を行う」ことでした。
また、今回の解析対象は、数式モデルの算出が困難な非線形システムでした。
つまり「深層学習で非線形システムの数式モデルMyChain(x)を算出」＝「深層学習で非線形システムの入出力関係を把握！」⇒「システムの特性を解析できた！」となります。
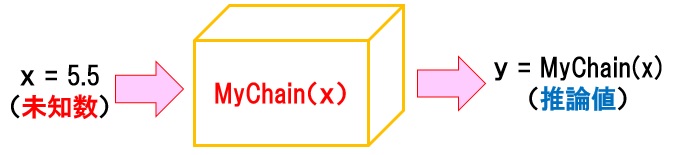
上図のような非線形システムを模擬した数式モデル『MyChain(x)』を生成するために、学習（重みを自動調整）を実施します。
【豆知識】モデルとは
今まで、特に説明もなく「モデル」という言葉を使ってきましたが、本記事で使われるモデルとは、プラモデルと同じ意味です。
つまり、「本物に似せたもの」という意味です。
そのため「システムの数式モデル」というのは、言い換えれば、「システムを模擬した数式」という意味です。
PCシミュレーションなどでは、この数式モデルを使って様々な解析を行います。
学習（非線形回帰モデル生成）
いよいよ『MyChain(x)』を生成するための学習（重みの自動調整）を実施します。
本稿では、学習プロセスの細かい説明はしません。ただし、簡単なイメージだけは説明したいと思います。
学習プロセル概要
人が何かを学ぶとき、人（教師など）から教わるか、本やネットで勉強するのが一般的です。このプロセスは深層学習でも同じです。学習を進めるには”教師データ”が必要です。
今回の場合、実験データｘに対するyの値が教師データとなります。
x=0の入力に対し、解析対象のシステムは、y=0.93..を出力していました。x=1のときは、y=0.72..で、x=9のときはy=0.42でした。
x=0~9(整数)を『MyChain(x)』に入力したとき、実際のシステムと同じ出力yを推論できれば、システムの数式モデル『MyChain(x)』が生成できた！と言えます。
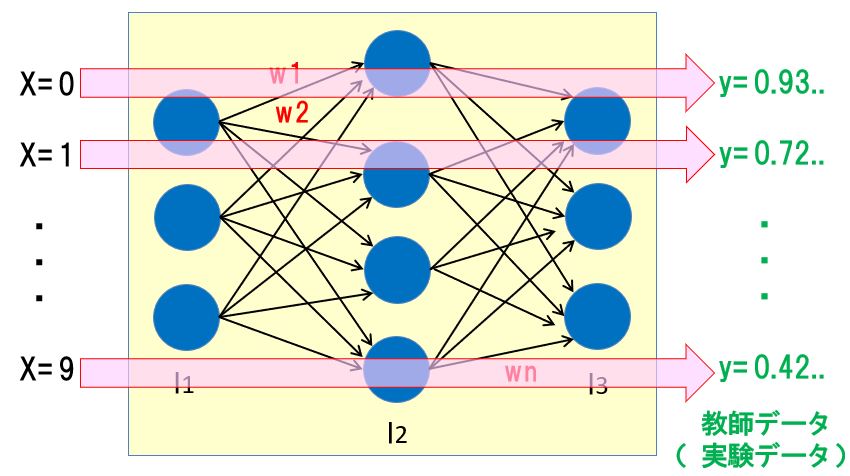
つまり、上図のように、入力xがニューラルネットワークを通過するとき、解析対象のシステムと同じ出力yを推論できるように、重みw1～wnを自動調整するのです。
今回のように教師データ（訓練データとも呼ぶ）を使う深層学習のことを、教師あり深層学習と呼びます。多くの場合、深層学習といえば、教師あり深層学習を指すため、”教師あり”は省略することが多いです。一方、教師なし深層学習もありますが、本記事では説明しない。
【実践】深層学習
学習は以下のソースコードで実施します。
最初に１万回学習させたのですが、精度が悪かった（lossがあまり下がらなかった）ので、8万回 学習させました！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
# 損失関数の計算（二乗誤差(MSE)を採用） def forward(x, y, model): t = model.predict(x) loss = F.mean_squared_error(t, y) return loss # 最適化アルゴリズムにAdamを採用 optimizer = optimizers.Adam() optimizer.setup(model) # 学習を繰り返す loss_list = [] step = [] for i in range(0, 80000): # 10000 loss = forward(x, y, model) step.append(i) loss_list.append(loss.data) # print("loss: {}".format(loss.data)) optimizer.update(forward, x, y, model) # 学習過程のグラフ plt.plot(step, loss_list) plt.title("Training Data") plt.xlabel("step") plt.ylabel("loss") plt.grid(True) plt.show() # 学習過程グラフを一部拡大 plt.plot(step, loss_list) plt.xlim([50000,56000]) plt.ylim([0,0.02]) plt.title("Training Data") plt.xlabel("step") plt.ylabel("loss") plt.grid(True) plt.show() |
lossの説明も割愛しますが、今回のような回帰モデル生成の場合は、lossが低ければ低いほど良い学習結果という点だけは覚えておいてほしい。
(”過学習”や”汎化と特化”の話しも控えます。一気に説明すると混乱させそうなので…)
今回の学習過程（lossが下がる様子）をグラフ化したものが以下です。左図は全体の学習過程、右図はlossが急速に下がった所を拡大したものです。
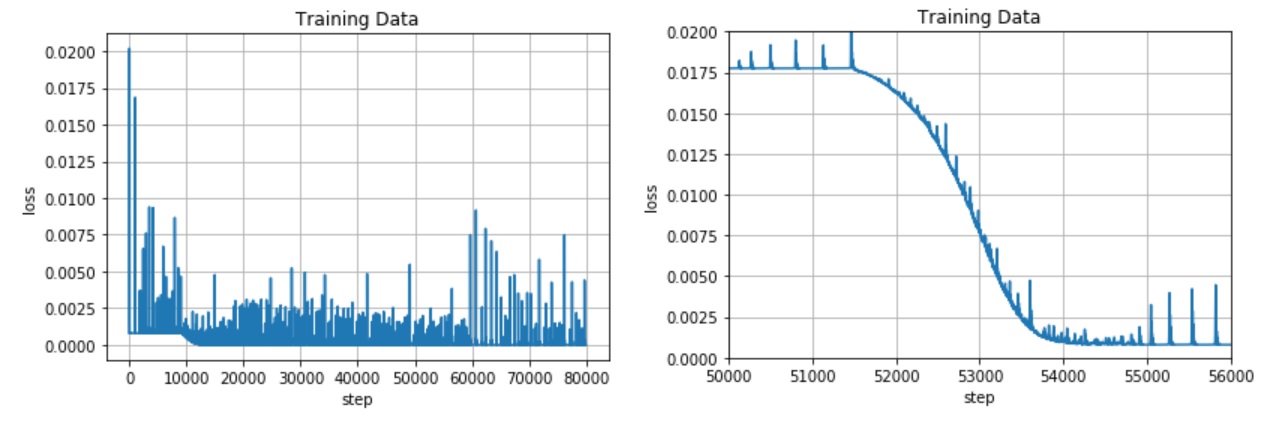
１万回の学習で精度が悪かったのは、６万回以上学習しないと、lossが下がりきらなかったからかぁ
…で！正直に言えば、何故このタイミングでloss値が下がったのか分かりません！！
ただし、この事実から分かることは、１万回の学習でダメでも６万回学習すれば、loss値は下がる！かも(?)ということ。まるでドリカムの歌のよう
lossが収束したと思ってから、さらに学習を行うことでlossが下がることもある。
推論
↑の学習で、ついに学習済みニューラルネットワーク（学習済みモデル）を生成できました！
この学習済みモデルが、ちゃんと解析対象のシステムと同じ出力を推論できるのか、下記のソースコードでテストします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# 教師データ(実験データ) plt.plot(x.data, y.data) plt.title("Training Data") plt.xlabel("x axis") plt.ylabel("y axis") plt.grid(True) plt.show() # 推論結果 ym = model.predict(x) plt.plot(x.data, ym.data) plt.title("Predict") plt.xlabel("input x") plt.ylabel("output ym") plt.grid(True) plt.show() # 推論結果2 xt = [[0.5], [1.8], [2.3], [3.3], [4.5], [6.8], [7.2], [7.7], [8.0], [8.2]] xt = Variable(np.array(xt, dtype=np.float32)) yt = model.predict(xt) plt.plot(xt.data, yt.data, "ro") plt.title("Predict2") plt.xlabel("input xt") plt.ylabel("output yt") plt.grid(True) plt.show() # グラフを重ねる plt.plot(x.data, y.data) plt.plot(x.data, ym.data) plt.plot(xt.data, yt.data, "ro") plt.title("comparison") plt.xlabel("input") plt.ylabel("output") plt.grid(True) plt.show() n = [[5.5]] n = Variable(np.array(n, dtype=np.float32)) yn = model.predict(n) print(yn) |
以下の左図が解析対象のグラフ、右図がx=0~9(整数)を『MyChain(x)』に入力したときの推論グラフです。
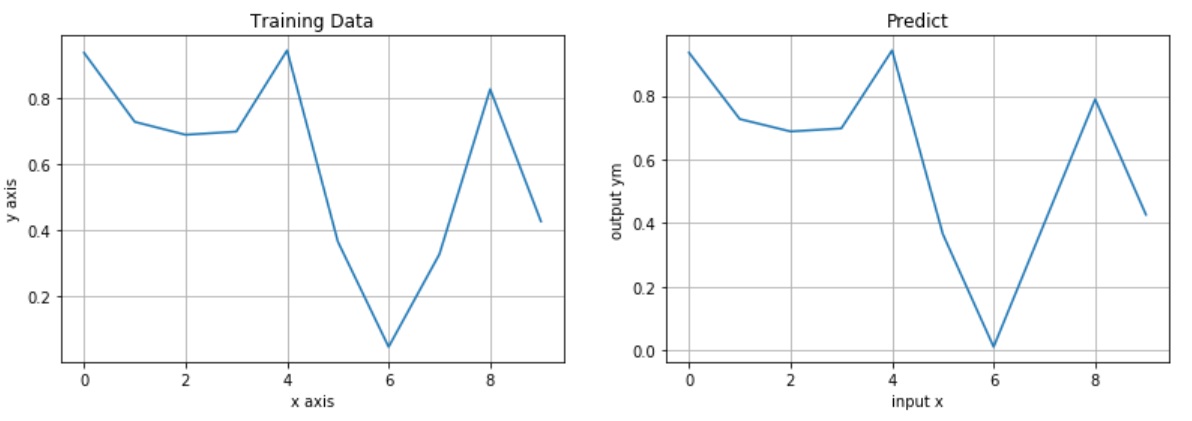
おお！ほとんど一緒じゃーん！ばっちり推論できてる！！…と思いますよね？
学習で使ったx=0~9(整数)の入力に対する出力ｙが推論できるのは当然でしょ！…と考える人もいると思いますので…
よし！学習で使用していない未知のx(少数)に対するyの推論結果も確認しましょう↓
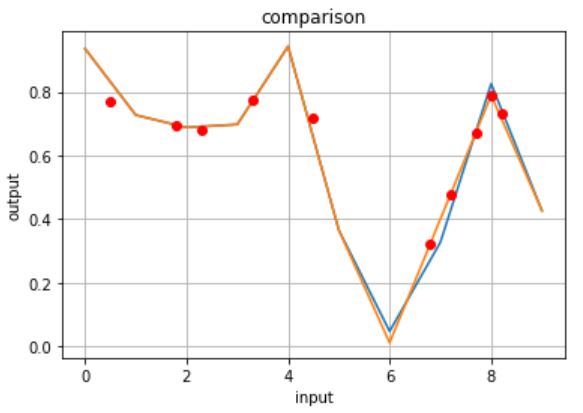
青グラフが解析対象・橙グラフがx(整数)をMyChainに入力したときの推論結果・赤プロットがx(少数)をMyChainに入力したときの推論結果です。
…深層学習すごい！！本当にMyChainが非線形システムの数式モデルになってる！
満足いく学習済みモデルができたら、保存しておき、次回からは学習なしで、いきなり推論から実施できるようにしましょう！
なお、本記事では、学習モデルの保存方法は割愛します。（機会があれば別記事で書くかも…）
深層学習で非線形システムの出力を推論できる！！
はやぶさの技術ノート
本記事を書く前に、Jupyter Notebookで検証を行った『メモ付きソースコード（技術ノート）』があるので、公開します。
ローカル環境で検証↓
Colaboratoryで検証↓
ちょっち散らかってるけど、ソースコード見るだけなら、技術ノートの方が便利だと思うので公開します。
まとめ
本記事で、『深層学習で非線形回帰モデルの生成』する方法を説明しましたが、これだけ説明すると、数学の教科書になりそうだったので…
用いる技術そのままで『深層学習でシステム解析する方法』というストーリーで説明しました。
また、今回は「制御で使うためのシステム解析」という課題でしたが、システム解析ができるということは、「以下のことが深層学習で実現できる」という可能性を秘めているということです。
- ブラックボックス解析
- リバースエンジニアリング
- 実験データの補間（未知の入力に対する出力の推論）
など（他にもあるかな？）
今、あなたが抱えている課題も深層学習で解決できるかもしれませんよ？
某企業でディープラーニング普及に奮闘した、ディープラーニングお兄さんは、本記事で日本のディープラーニングお兄さんになれたかな？
本記事を読んで「深層学習で課題が解決できた！」・「深層学習についてをもっと勉強したい！」という人が現れたら、ディープラーニングお兄さんはすごく嬉しい！
↓この本おすすめ！
