こんにちは。
ディープラーニングお兄さんの”はやぶさ”@Cpp_Learningだよー
本サイトで機械学習の記事などを書いています。
嬉しいことに本サイトに遊びに（勉強しに）きてくれる読者が少しづつ増えています！
本サイトで特に人気なのが、以下の【深層学習入門】シリーズみたいです(*･ω･)ﾉ♪
【第１弾】
【第２弾】
本記事は【深層学習入門】シリーズの第３弾！
『超実践！ChainerのDefine by Runで動的ニューラルネットワーク設計』について説明したいと思います。
本サイトをきっかけに
という人が増えると嬉しいなぁ(*･ω･)ﾉ♪
説明とか不要だからソースコードだけ見せて！という人は目次から『はやぶさの技術ノート』にジャンプして下さい。
Contents
前置き
本題に入る前に、本記事の概要を先に説明しておきます。
本記事では、冒頭でも紹介した以下の記事と同じ課題『深層学習でシステム解析する方法』について説明します。
※以降↑の記事のことを前回の”NN設計”記事と呼びます。多用するので覚えてね！
と思ったかもしれませんが、前回の”NN設計”記事でも説明した通り「深層学習は奥深い」ということを伝えるために、あえて同じ課題を使います！
また、前回 説明しきれなかった”活性化関数”が本記事ではキーワードとなるので、気になる人は続きを読んで下さいね(*･ω･)ﾉ♪
本記事は、前回の”NN設計”記事を読んでいる前提で説明をします。そうじゃないと「深層学習は奥深い」というか「ニューラルネットワーク設計の違い」を楽しめないので…まだ読んでいない人は読んでから、本記事の続きに進んでね！
以降から本題に入ります！
Define and Run と Define by Run
ニューラルネットワーク設計は、【Define and Run】と【Define by Run】という２つの手法に分類できます。両者の違いは以下の通りです。
【Define and Run】
- 静的なニューラルネットワーク
- ニューラルネットワークを固定(定義)⇒そのニューラルネットワークにデータを流して演算を行う
【Define by Run】
- 動的なニューラルネットワーク
- データを流しながらニューラルネットワークの固定(定義)と演算を行う
前回は【Define and Run】つまり静的ニューラルネットワーク設計をしました！
今回は【Define by Run】つまり動的ニューラルネットワーク設計で前回と同じ課題『深層学習でシステム解析』を行います！
というのが気になってきましたよね？後で丁寧に説明しますので、ここでは【Define and Run】と【Define by Run】の言葉の定義を覚えて下さいね。
ニューラルネットワーク設計は【Define and Run】と【Define by Run】という２つの手法があり、ニューラルネットワークの定義の仕方で区別できます。
【復習】課題の確認 -システム解析とは-
前回の”NN設計”記事でも説明済みですが、今回やりたいこと（課題）について簡単に説明しておきます。
「あるブラックボックスのシステムを解析したい！」
言い換えれば
「解析対象であるシステムの特性を知りたい！」
と思ったら、その対象の数式モデルを生成することで、特性を明らかにできます。
数式モデルを生成する１つの方法は、以下の通りです。
【数式モデルの生成方法】
- 解析対象のシステムに複数の適当な入力値xを与え、出力値ｙを観測
- 各xとyの相関から数式モデルを生成
例えば、解析対象のシステムに入力値x=0~9(整数)を与えたときの出力値yを観測した結果が以下だったとします。
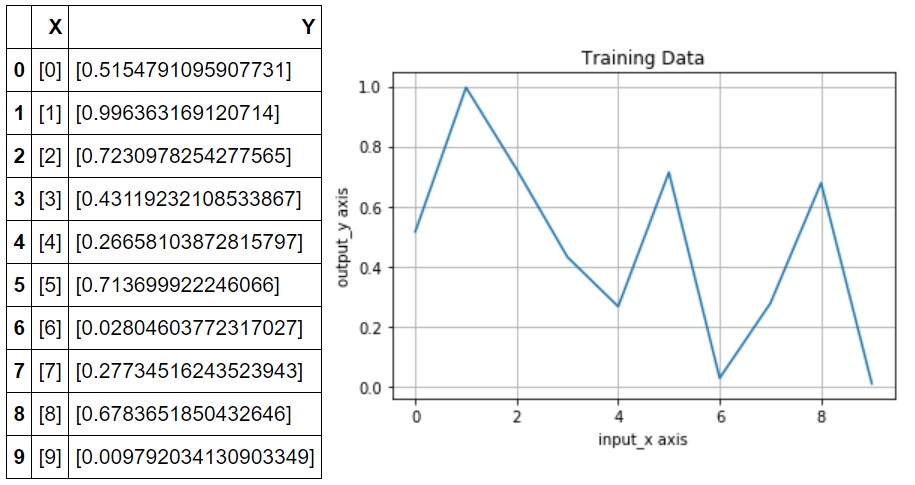
こんな不規則なデータのxとyの相関なんて分からないよ…
非線形システムの数式モデルなんて算出できない！となります(´；ω；｀)
このような問題の解決に深層学習を使います。
【課題】：非線形システムの解析（非線形回帰モデルの生成）
【解決手段】：深層学習
活性化関数とは
動的ニューラルネットワーク設計について説明する前に、今回のキーワード”活性化関数”を先に説明します。
ニューラルネットワークの”ノード”と”層”については前回の”NN設計”記事で説明しました。実は下図のL1～L2層の各ノードは”活性化関数”を持っていました。
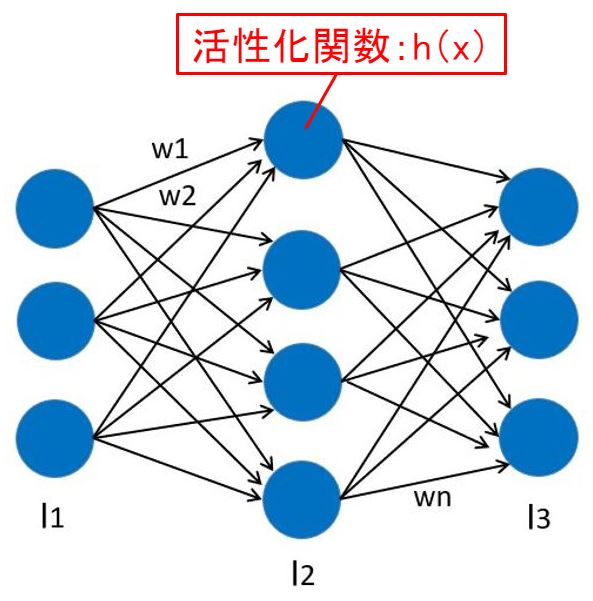
深層学習では、左から伝播してきた情報を次のノードへ伝播させながら学習および推論をするのですが…
伝わってきた情報を”そのまま”伝播させず、”活性化関数で演算した結果”を伝播させます。
このように「活性化関数で演算した結果を伝播」＝「発火」と呼ばれています。
中間層の各ノードは”活性化関数”を持っています。
活性化関数のイメージ
活性化関数のイメージを私なりの言葉で伝えてみます。
例えば「アイデアをひらめく！」をもう少し直観的な表現にすると…
- 脳内に電流が流れる
- 電球が点灯する
- 脳内が発火する
- 脳内がビリっときた
なんて表現を使いますよね？このような感覚を数式で表現したものが”活性化関数”です。
”脳内に電流が流れる”とかニューラルネットワークっぽいよね！（←ちょっと強引？）
活性化関数の役割
いつでも！どこでも！”アイデアがひらめく”と嬉しいけど、そんなに都合よくいかないですよね？
とか
なんて体験したことありますよね？こんな感覚を活性化関数で表現できます。
例えば、前回の”NN設計”記事で採用した“relu”という活性化関数:h(x)を可視化したのが下図です。
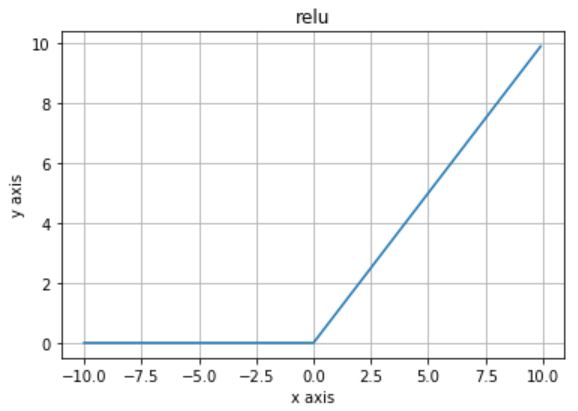
“relu”にx < 0のマイナス値が入力されると、出力がy = 0になります。つまり、マイナス値の情報が入力されたときは、次のノードにその情報を伝播させないということです。
私なりの”relu”に対する直観的な解釈は「マイナス値」＝「ノイズ」つまり上記の
- 勉強を始めたばかりの頃は理解できなかった
- 初めて挑戦するような仕事はトラブルの連続
といった”ひらめき”から遠いマイナスの情報をカットしている！と考えています。
上記した”活性化関数”や”relu”に対する直観的な解釈は、私オリジナルの説明ですが、本や記事でも例えは違いますが「マイナス値であるノイズをカット！」と説明しているものが多いです。
私の活性化関数や”relu”に対する直観的な理解が正解/不正解というのは、実は分かっておらず…
ニューラルネットワーク設計で「”relu”を使うとなぜか上手く学習できる！」という事実に対し、数学的な根拠があまりないらしい…
（私が知らないだけかもしれないが…）
ニューラルネットワーク設計で活性化関数に”relu”を採用すると、上手く学習できる！ということは分かっていますが、数学的根拠は不明確らしい。
ニューラルネットワークの設計コンセプト
今回は動的なニューラルネットワークの設計なので…
- 何を
- どんな条件で
- 動的にするのか
という設計コンセプトを説明してから、設計（実装）を行います。
設計コンセプト検討❶ -活性化関数-
上記した通り、ニューラルネットワーク設計では、活性化関数に”relu”を採用するのが定石となっています。
しかし、私の直観的な理解が正しいとすれば、”relu”を採用することで…
『”ひらめき”から遠いマイナスの情報がカットされる！』ことを意味します。
でも『マイナスの情報を完全に除去するって…なんか勿体なくないですか？』
うまく言えないけど、マイナスの情報とはいえ完全になかったことにするなんて…
- 勉強で苦しいとき！
- 遠回りした解決策！
- マイナスからのスタート！
これらのマイナス情報から得られるものって必ずあると思うんだよなぁ
ということで”leaky_relu”と呼ばれる活性化関数を使い、マイナスの情報も伝播できるようにニューラルネットワークを設計します！
下図は“leaky_relu”という活性化関数:h(x)を可視化したものです。
設計コンセプト検討❷ -ニューラルネットワークの構造-
突然ですが…子供の成長スピードは早い！最初は私を怖がっていたのに、安全な人だと学習すると、笑顔を見せてくれます（まだ小さい姪っ子が可愛い）
子供なら、成長と同時に脳内のニューロンが増えたり・減ったり・変化したりすると思いますが…
大人になると身体的な成長が小さい（ほぼ無い？）ので、脳内のニューロン構造ってある程度、固定されてると思っています。（←なんとなくね）
でも、大人でも”アイデアをひらめく”ことがある！
これって『いつもと違う活性化関数が働いたのかなぁ』とか考えてしまった！
- 大人の脳⇒ニューロン構造固定⇒ニューラルネットワーク固定
- 大人の脳でも閃く⇒閃く前後でニューロン構造が変化したとは考えにくい？⇒活性化関数が違うのかも！
みたいなことを、お風呂でリラックスしているときに”ひらめいた”
つまり、ニューラルネットワークの構造（ノードの配置）はそのままで、活性化関数を動的に変化させるだけで、前回より精度の良い推論結果になるだろう！という仮説を立てました。
仮説⇒実装⇒検証を行うことが重要だ！って探偵ガリレオの湯川先生が言ってた！
設計コンセプト検討➌ -情報整理-
以上の設計コンセプト検討❶❷の情報を整理する
- 何を ⇒ 活性化関数を
- どんな条件で ⇒ ”ひらめいた”とき
- 動的にするのか ⇒ 切り替える
というアイデアの実装方法を検討する。
”ひらめいた”ときが抽象的過ぎて実装できないので、もう少し噛砕いて数値で表現したい…
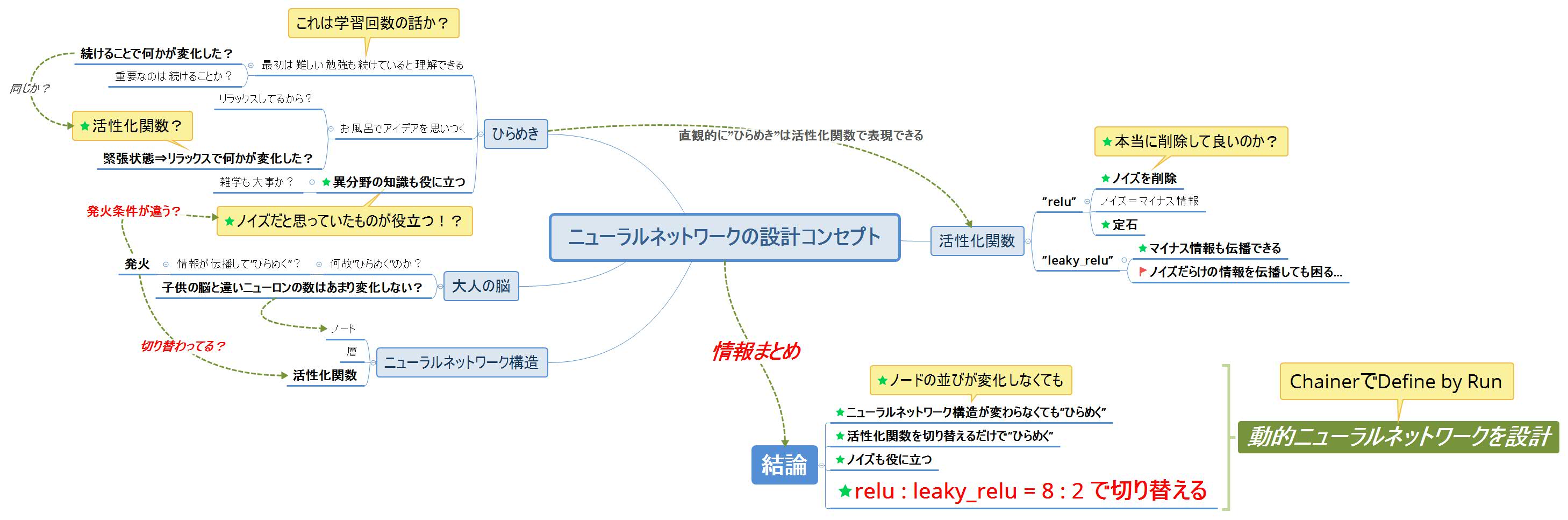
（マインドマップまで公開しなくても良かったかな？まぁ参考になるかもしれないし良いか？）
マインドマップで脳内を可視化し”思考”を発散させた結果をもとに要点をまとめる。
【要点まとめ】
- ニューラルネットワーク構造（ノードの並び）を固定しても”ひらめく”
- 活性化関数を切り替えるだけで推論の精度は上がると予想
- マイナス情報（ノイズ）も役に立つ
- ノイズばかり伝播しても困る
- ”ひらめき”＝普段と異なる発想
- ”ひらめき”を活性化関数の切り替えで表現
【結論】
『relu ： leaky_relu ＝ ８：２』の割合で動的に切り替える！
設計コンセプト確定
最終的には実装を意識した具体的な設計コンセプトに仕上げた。
【動的ニューラルネットワークの設計コンセプト】
- 基本的に活性化関数は”relu”を採用
- 乱数を使い 約20%の確率で活性化関数を“leaky_relu”に切り替える
- ニューラルネットワーク構造（ノードの並び）は前回と同じ構造を採用
つまり、以下のイメージの動的ニューラルネットワークを設計します。
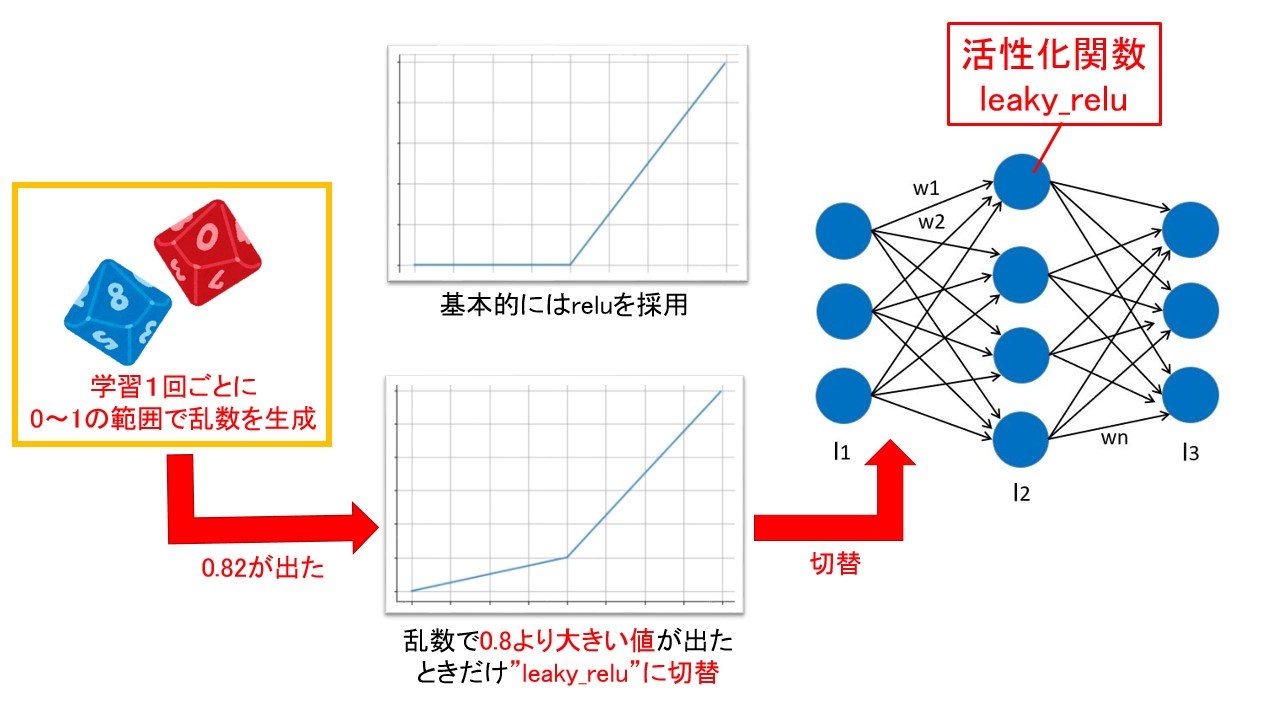
設計コンセプトも決まったので、あとは実装するだけですね！
何かを検討するとき、マインドマップ描いて、脳内を可視化することで”思考”を整理するのがオススメです。
【超実践】Chainerと深層学習で非線形回帰モデル生成 -Define by Run-
前回同様に、今回も国産の深層学習フレームワーク”Chainer”を使います。
”Chainer”は世界で初めて【Define by Run】の仕組み取り入れた深層学習フレームワークです。
今では他のフレームワークでも【Define by Run】の仕組み取り入れていますが、数年前は動的ニューラルネットワークを設計できる深層学習フレームワークはとても貴重な存在でした！
”Chainer”大好き！今回も”Chainer”の開発者様に感謝しつつ実践で使わせて頂きます！
環境構築
環境構築については、前回の”NN設計”記事で説明済みなので割愛します。以降からソースコードを交えて、動的ニューラルネットワーク設計について説明します。
import
数値演算やChainer用のモジュールなどをimportします。
|
1 2 3 4 5 6 7 8 9 10 |
import math import random import numpy as np import pandas as pd import matplotlib.pyplot as plt from chainer import Chain, Variable import chainer.functions as F import chainer.links as L from chainer import optimizers |
動的ニューラルネットワーク設計
オリジナルの動的ネットワーク『MyChain』を設計！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class MyChain(Chain): def __init__(self): super(MyChain, self).__init__( l1 = L.Linear(1, 100), l2 = L.Linear(100, 50), l3 = L.Linear(50, 1) ) def predict(self, x, sw_func): if sw_func == 1: h1 = F.leaky_relu(self.l1(x)) h2 = F.leaky_relu(self.l2(h1)) else: h1 = F.relu(self.l1(x)) h2 = F.relu(self.l2(h1)) return self.l3(h2) |
今回は【Define by Run】なので、以下の設計ポイントがあります。
- スイッチのON/OFFのように活性化関数を切り替えられるように設計
- スイッチのON/OFFを柔軟に切り替えられるように、引数:sw_funcでスイッチのパラメータを受け取る
NNモデル宣言
↑で設計したネットワーク構造を使います！と宣言した後、いよいよ学習を行います。実は↑のネットワーク…まだ中身空っぽなんです。（生まれたてのベイビーなので）
|
1 2 3 |
# NNモデルを宣言 model = MyChain() print(model) |
実験データ生成
非線形システムを模擬した実験データ(ダミー)を乱数で生成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 実験データ用の配列 x = [] y = [] get_values = 0 for i in range(10): get_values = random.random() x.append([i]) y.append([get_values]) # データフレーム生成(列基準) df = pd.DataFrame({'X': x, 'Y': y}) # グラフ出力 plt.plot(x, y) plt.title("Training Data") plt.xlabel("input_x axis") plt.ylabel("output_y axis") plt.grid(True) df |
既にお見せしている、以下のデータが生成できました。
乱数を使って実験データ（ダミー）を生成しているため、このソースコードを再実行すると全く違う入出力が得られます。
Chainer用に変換
実験データx, yをChainerで使えるようにnumpy配列のfloat32に変換します。
|
1 2 |
x = Variable(np.array(x, dtype=np.float32)) y = Variable(np.array(y, dtype=np.float32)) |
学習
”MyChain”を学習させ、未知の入力値xに対する出力値yを推論できるようします！
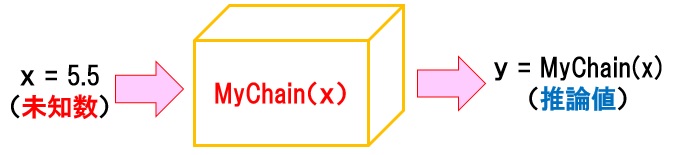
前回同様、8万回 学習させます！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
rand_val = 0 sw_func = 0 log_sw = [] # 損失関数の計算（二乗誤差(MSE)を採用） def forward(x, y, model): # 活性化関数の切替 rand_val = np.random.random() if rand_val > 0.8: sw_func = 1 else: sw_func = 0 log_sw.append([sw_func]) t = model.predict(x, sw_func) loss = F.mean_squared_error(t, y) return loss # 最適化アルゴリズムにAdamを採用 optimizer = optimizers.Adam() optimizer.setup(model) # パラメータの学習を繰り返す loss_list = [] step = [] for i in range(0, 80000): # 10000 loss = forward(x, y, model) step.append(i) loss_list.append(loss.data) # print("loss: {}".format(loss.data)) optimizer.update(forward, x, y, model) # 学習過程 plt.plot(step, loss_list) plt.title("Training Data") plt.xlabel("step") plt.ylabel("loss") plt.grid(True) plt.show() |
このコードで活性化関数の動的な切替を実現しています。ポイントは以下の通りです。
0～1の範囲で乱数を生成し
- 0.8より大きな値なら：ON（leaky_relu）
- それ以外の値なら：OFF（relu）
となるように引数の”sw_func”を操作し”活性化関数”を動的に切り替えながら学習させます。
考察
”活性化関数の切替”および学習過程の”lossが下がるところ”を確認！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 学習過程グラフを一部拡大 plt.plot(step, loss_list) plt.xlim([10000, 20000]) plt.ylim([0,0.1]) plt.title("Training Data") plt.xlabel("step") plt.ylabel("loss") plt.grid(True) plt.show() # 活性化関数の切替 plt.plot(log_sw) plt.xlim([0,50]) plt.ylim([0,1.5]) plt.title("Activation Function") plt.xlabel("step") plt.ylabel("Random") plt.grid(True) plt.show() |
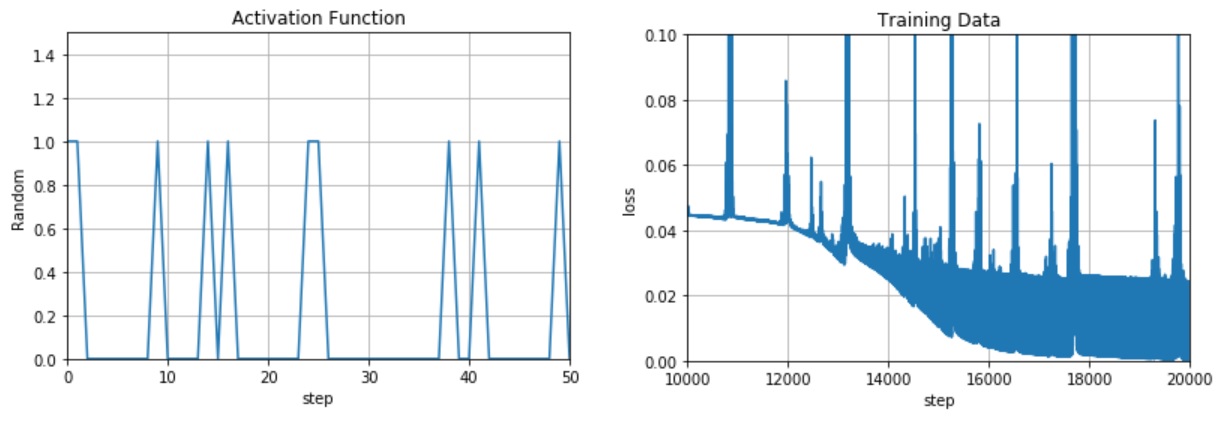↑左のグラフが”活性化関数の切替”を可視化したものです。良い感じにランダムで切り替わってますね（まるで私の脳内のようだ！？）
↑右のグラフが”学習過程”を可視化したものです。すごいノイズが乗ってるけど、学習回数1万回超えたあたりから、lossが急降下してます！（前回は6万回付近でlossが急降下した）
前回は見られなかった現象です。偶然かもしれないけど、”活性化関数の切替”で学習回数が大幅に減る可能があるのは興味深いね！
別の対象でも何回か試してみたけど、”活性化関数の切替”で学習回数が大幅に減る傾向があることを確認しました。
（これひょっとして、すごい発見なんじゃ…）
サンプル数不足（検証不足）なので断定は控えますが、”活性化関数の切替”に可能性を感じますね(*･ω･)ﾉ♪
仮説⇒実装⇒検証を実施した結果、”活性化関数の切替”に可能性を感じています！
推論
学習により自動調整された”重み：W1~Wn”は固定されますが、推論でも活性化関数を切り替えることができます。
なので今回は…
- ”leaky_relu”に固定
- ”relu”に固定
- ”leaky_relu”と”relu”を条件付きで切り替える
の3パターンで推論を行ってみます！
推論結果❶
活性化関数を”leaky_relu”に固定
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# 教師データ(実験データ) plt.plot(x.data, y.data) plt.title("Training Data") plt.xlabel("x axis") plt.ylabel("y axis") plt.grid(True) plt.show() # 推論結果 sw = 1 ym = model.predict(x, sw) plt.plot(x.data, ym.data) plt.title("Predict") plt.xlabel("input x") plt.ylabel("output ym") plt.grid(True) plt.show() # 推論結果2 xt = [[0.5], [1.8], [2.3], [3.3], [4.5], [6.8], [7.2], [7.7], [8.0], [8.2]] xt = Variable(np.array(xt, dtype=np.float32)) yt = model.predict(xt, sw) plt.plot(xt.data, yt.data, "ro") plt.title("Predict2") plt.xlabel("input xt") plt.ylabel("output yt") plt.grid(True) plt.show() # グラフを重ねる plt.plot(x.data, y.data) plt.plot(x.data, ym.data) plt.plot(xt.data, yt.data, "ro") plt.title("comparison") plt.xlabel("input") plt.ylabel("output") plt.grid(True) plt.show() n = [[5.5]] n = Variable(np.array(n, dtype=np.float32)) yn = model.predict(n, sw) print(yn) |
青グラフが解析対象・橙グラフが学習で使用した入力値x(整数)の推論結果・赤プロットが未知の入力値x(少数)の推論結果です。
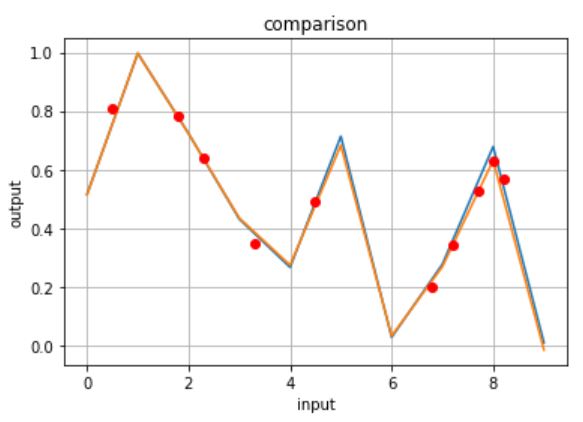
…深層学習すごい！！今回設計した『MyChain』で非線形システムの特性を把握できるようになりました。
良好な推論結果が得られたのは、活性化関数を”leaky_relu”固定にしたからなのか？を確認するために、同様の検証を”relu”固定で実施します。
推論結果❷
活性化関数を”relu”に固定
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# 教師データ(実験データ) plt.plot(x.data, y.data) plt.title("Training Data") plt.xlabel("x axis") plt.ylabel("y axis") plt.grid(True) plt.show() # 推論結果 sw = 0 ym = model.predict(x, sw) plt.plot(x.data, ym.data) plt.title("Predict") plt.xlabel("input x") plt.ylabel("output ym") plt.grid(True) plt.show() # 推論結果2 xt = [[0.5], [1.8], [2.3], [3.3], [4.5], [6.8], [7.2], [7.7], [8.0], [8.2]] xt = Variable(np.array(xt, dtype=np.float32)) yt = model.predict(xt, sw) plt.plot(xt.data, yt.data, "ro") plt.title("Predict2") plt.xlabel("input xt") plt.ylabel("output yt") plt.grid(True) plt.show() # グラフを重ねる plt.plot(x.data, y.data) plt.plot(x.data, ym.data) plt.plot(xt.data, yt.data, "ro") plt.title("comparison") plt.xlabel("input") plt.ylabel("output") plt.grid(True) plt.show() n = [[5.5]] n = Variable(np.array(n, dtype=np.float32)) yn = model.predict(n, sw) print(yn) |
先ほど同様、青グラフが解析対象・橙グラフが学習で使用した入力値x(整数)の推論結果・赤プロットが未知の入力値x(少数)の推論結果です。
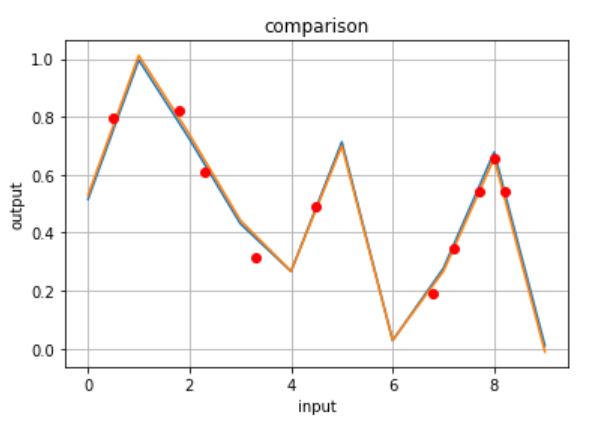
ほう！興味深い！！
推論結果❶❷を観測すると…
- 入力値x > 5 のとき”relu”の方が推論精度が良い
- 入力値x <= 5 のとき”leaky_relu”の方が推論精度が良い
という結果が得られた。（僅差だけどね！）
この知見をそのまま条件にして、”活性化関数”を切り替えながら推論を行ってみる。
僅かな違いを見逃さなければ、得られる知見がある！
推論結果❸
入力データに応じて、活性化関数を”relu”と”leaky_relu”を切り替える。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
# 教師データ(実験データ) plt.plot(x.data, y.data) plt.title("Training Data") plt.xlabel("x axis") plt.ylabel("y axis") plt.grid(True) plt.show() # 推論結果 ym = model.predict(x, sw) plt.plot(x.data, ym.data) plt.title("Predict") plt.xlabel("input x") plt.ylabel("output ym") plt.grid(True) plt.show() ''' # 推論結果2 xt = [[0.5], [1.8], [2.3], [3.3], [4.5], [6.8], [7.2], [7.7], [8.0], [8.2]] xt = Variable(np.array(xt, dtype=np.float32)) yt = model.predict(xt, sw) plt.plot(xt.data, yt.data, "ro") plt.title("Predict2") plt.xlabel("input xt") plt.ylabel("output yt") plt.grid(True) plt.show() ''' # 推論結果3 -入力値から活性化関数を変更- # log_xi = [] # log_yi = [] sw_i = 0 for i in range(10): tmp = random.uniform(0.0, 9.0) xi = [[tmp]] xi = Variable(np.array(xi, dtype=np.float32)) if xi.data > 5: sw_i = 1 print('xi = {} ⇒ reluを選択'.format(xi)) else: sw_i = 0 print('xi = {} ⇒ leaky_reluを選択'.format(xi)) yi = model.predict(xi, sw_i) plt.plot(xi.data, yi.data, "bo") # plt.title("Predict3") # plt.xlabel("input xi") # plt.ylabel("output yi") # plt.grid(True) # plt.show() # グラフを重ねる plt.plot(x.data, y.data) plt.plot(x.data, ym.data) # plt.plot(xt.data, yt.data, "ro") # plt.plot(xi.data, yi.data, "go") plt.title("comparison") plt.xlabel("input") plt.ylabel("output") plt.grid(True) plt.show() n = [[5.5]] n = Variable(np.array(n, dtype=np.float32)) yn = model.predict(n, sw) print(yn) |
この検証では、ズルできないように入力値x（青プロット）を乱数で生成し、推論を行いました。
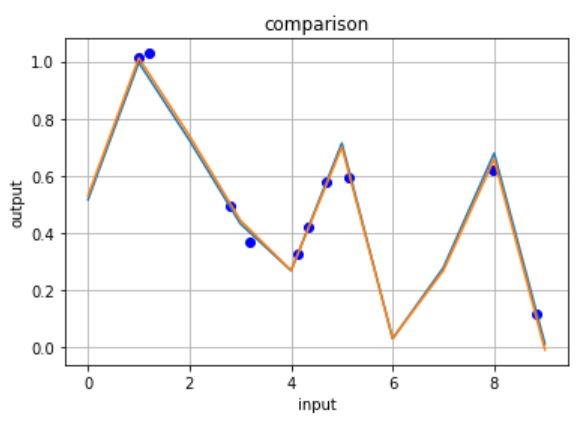
…ちょっと怖いくらい精度良いですね！笑
学習だけでなく、推論でも”活性化関数”を動的に切替られます。
はやぶさの技術ノート
本記事を書く前に”Jupyter Notebook”で検証を行った『メモ付きソースコード（技術ノート）』があるので公開します。
ローカル環境で検証↓
Colaboratoryで検証↓
下書きなので少し雑なところもありますが、ソースコード見るだけなら『技術ノート』の方が便利だと思うので公開します。
まとめ
人生で初めて動的ニューラルネットワーク設計に挑戦してみましたが、深層学習の”楽しさ”と”奥深さ”を再確認しました！！
本記事で説明した【Define by Run】のポイントをまとめ
【Define by Run ポイント】
- 活性化関数を切り替えられる
- ネットワーク構造を切り替えられる
- 切替の条件も設定できる
- 切替えの設定は自作ネットワーク『MyChain』Class内外どちらでも可
- 『MyChain』Class外から切替の条件を引数で渡せる
- 学習だけでなく、推論でも Define by Run！
今回は、活性化関数のみ動的にしましたが、ネットワーク構造（ノード数や層の深さ）も動的にできます！
また、８：２という直観で活性化関数を切り替えましたが、もっと論理的な条件で切り替えても面白いかと！
さらに、今回あしようした以外の活性化関数もあります！
動的ネットワークの組み合わせは星の数ほどあります！！
私 1人では、すべての組み合わせを試すのは不可能です…
でも、本記事を読んくれた人は、動的ニューラルネットワークの設計方法を習得できたと思う！！
私に代わって、自分オリジナルのネットワーク『MyChain』を設計してほしい！！
本記事を参考に…
とか
なんて人が現れたディープラーニングお兄さんは最高に嬉しいです(*･ω･)ﾉ♪
奥が深い深ーーい！深層学習を思いっきり楽しんで下さいな！
（完）
おまけ -メッセージと設計ガイド-
時間に余裕のある人は読んでみてね↓
メッセージ
今回も良い記事だった～♪ららら～♪
どこからか楽し気な歌声が聞こえる！人気フクロウ”くるる”@kururu_owl の声だ！
…さっき歌ってたけどな！というツッコミはしないぞ！笑
Define by Runは自然言語処理で使えます！と説明している、良質な記事や参考書はあり、中にはソースコードまで載せているものもあります。
ただ、自然言語処理のチュートリアルはハードルが高い気がしており、入門レベルでDefine by Runを学べる記事があると良いのになぁ…と思い本記事を書きました。
役に立つと嬉しいなぁ
顔をブルブルと大きく横に振る”くるる”が今日も可愛い！
模範解答！？笑
私”はやぶさ”は研究・開発以外にメンター（プログラミングの後輩教育係）も担当しており、社内限定のチュートリアル記事も作っています。
メンターを担当する上で”答え”だけでなく”考え方”まで教えることが重要だと考えています。
そのため、所属とは関係のない本サイトでも、読者の技術者教育に貢献したい！という想いから…
『技術ノート(実装方法)』だけでなく、マインドマップなどの”考え方”まで説明しています。
勉強になるかな？なると嬉しいなぁ(*･ω･)ﾉ♪
設計ガイド -深層学習の勉強する順番-
うーん。どうしよう…”くるる”が悩んでいる様子。
！！！！びっくりして全身の羽毛が逆立つ！ そんな”くるる”も可愛い
はい！何にも問題ありません！結局のところ深層学習は「やってみないと分からない！」ということが多いです。
本記事で『仮説⇒実装⇒検証を行うことが重要！』と説明しましたが…
『実装⇒仮説⇒検証』でも問題ありません！本当に重要なのは…
- ”シグモイド”を採用した動的ネットワークを設計⇒学習
- ノイズが少ない
- ”シグモイド”のグラフが滑らかだから？
というプロセスでも良いです！あまり順番を気にせず自由に！楽しく！勉強してほしいぁ
設計ガイド -Chainerで使える活性化関数-
”くるる”大きく何度も頷いた後で質問してくれた。
やる気のある鳥 大好き！『Chainerで使える活性化関数』は以下の公式サイト（以下のボタン）から確認できます！
関数の数式やソースコードまで丁寧に説明してあります。
ただし、グラフまでは載っていないので技術ノートに『Chainerで使える活性化関数』を可視化するソースコードも載せておきました！活性化関数の選定などに、ご活用下さい！
楽しそうで何より！笑
”くるる”ちゃんのように自由に！楽しく！深層学習の勉強をして下さいね(*･ω･)ﾉ♪
（おまけ完）
↓この本おすすめ！
