こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
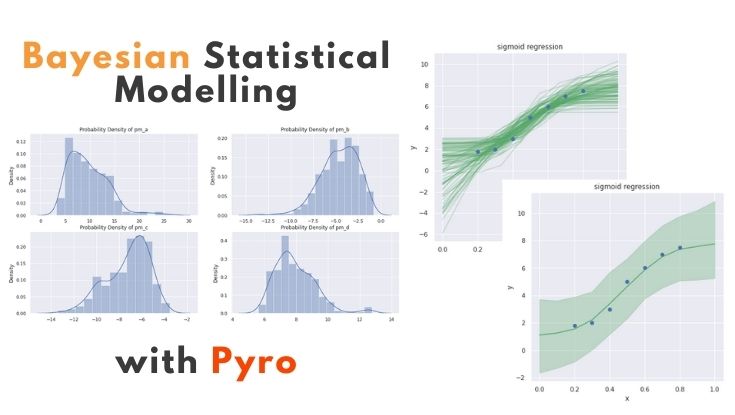
今回はPyroによる一般化線形モデル(GLM:generalized linear model)のベイズモデル化について勉強したので、備忘録も兼ねて本記事を書きます。
Contents
一般化線形モデル(GLM:generalized linear model)とは
一般化線形モデル(GLM)については、簡単にですが以下の記事で紹介済みなので、本記事では割愛します。

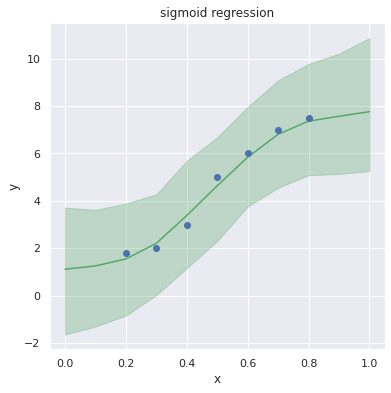
なお今回はリンク関数にシグモイド関数(sigmoid function)を採用した回帰モデルを設計します(下図参照)
一般化線形モデル(GLM)のベイズモデル化
最終的には複数のパラメータをもつGLMをベイズモデル化し、MCMCでパラメータの事後分布を推定するところまで実装します。
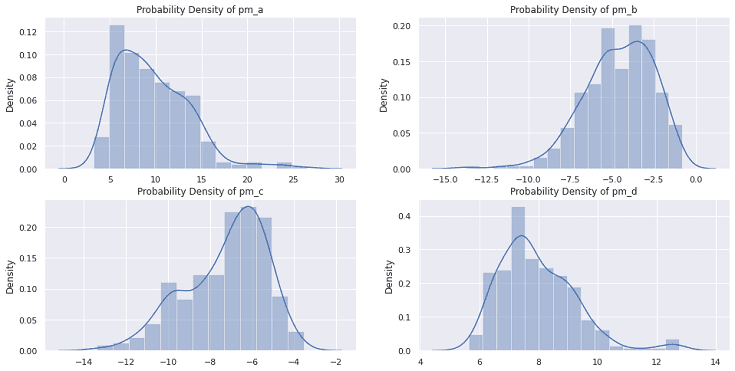
※今回の例では pm_a, pm_b, pm_c, pm_d の4つのパラメータが登場します
なお「GLMのベイズモデル化」というのは、以下の本の言葉をお借りしました。
実践!Pyroで一般化線形モデル(GLM)のベイズモデル化
PyroのMCMCはとても時間がかかるので、GPUの活用をオススメします。なお本記事のソースコードはGoogle Colabで動作確認しています。
Google Colabなら、タダでGPUが使えるし、以下のコマンドのみで環境構築完了です。
pip install pyro-ppl
以降からソースコード書いていきます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns import torch import torch.distributions.constraints as constraints import pyro import pyro.distributions as dist from pyro.infer.mcmc import MCMC,NUTS from pyro.infer import Predictive |
トイデータ作成
適当なトイデータを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# データ X = [0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8] Y = [1.8, 2.0, 3.0, 5.0, 6.0, 7.0, 7.5] # listからtorch.tensorに変換 Xt = torch.tensor(X) # 目的変数:Yt = [y0, y1, y2, ... yi] Yt = torch.tensor(Y) # 説明変数:Xt = [x0, x1, x2, ... xi] # 散布図で可視化 sns.set(style="darkgrid") fig = plt.figure(figsize=(6.0, 6.0)) plt.scatter(Xt, Yt) plt.xlabel('x') plt.ylabel('y') plt.xlim(0,1) plt.ylim(0,10) plt.title("Samples") plt.show() |
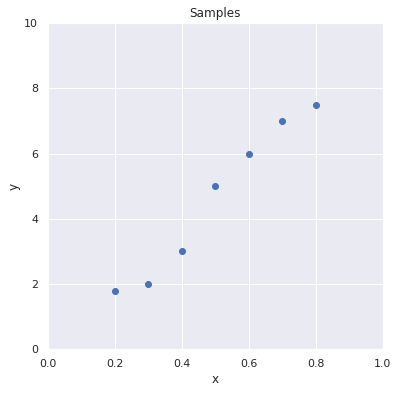
このデータが今回の対象です。
ベイズ統計モデリング
今回は以下のモデルを設計します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def model(X, Y=None): pm_a = pyro.sample('pm_a', dist.Normal(0.0, 10.0)) pm_b = pyro.sample('pm_b', dist.Normal(0.0, 10.0)) pm_c = pyro.sample('pm_c', dist.Normal(0.0, 10.0)) pm_d = pyro.sample('pm_d', dist.Normal(0.0, 10.0)) # sigmoid(x) = 1 / (1+e^-x) mu = pm_c * torch.sigmoid(-1.0 * (pm_a * X + pm_b)) + pm_d sigma = 1.0 pm_Y = pyro.sample('pm_Y', dist.Normal(mu, sigma), obs=Y) return pm_Y |
モデルの概要は以下の通りです。
【リンク関数】
f(x) = c * sigmoid(- 1 * (a * x + b)) + d
【確率分布】
μ = f(x), σ = 1.0
Y ~ Normal(μ, σ)
上記パラメータa,b,c,dが正規分布(事前分布)に従って発生すると考え、ベイズモデル化します。
【パラメータ(確率変数 ~ 事前分布)】
μ = 0, σ = 10
pm_a ~ Normal(μ, σ)
pm_b ~ Normal(μ, σ)
pm_c ~ Normal(μ, σ)
pm_d ~ Normal(μ, σ)
【モデル】
f(x) = pm_c * sigmoid(-1 * (pm_a * x + pm_b)) + pm_d
【確率分布(尤度)】
μ = f(x), σ = 1.0
Y ~ Normal(μ, σ)
MCMC実行
以下のコードでMCMCによる推論を実行します。
|
1 2 3 4 |
# Run MCMC kernel = NUTS(model) mcmc = MCMC(kernel, warmup_steps=600, num_samples=500) mcmc.run(X=Xt, Y=Yt) |
事後分布の可視化
MCMCで算出された各パラメータは以下のコードで取得できます。
|
1 2 3 4 5 6 |
# get param (num_samples=500) mcmc_samples = mcmc.get_samples() pm_a = mcmc_samples["pm_a"] pm_b = mcmc_samples["pm_b"] pm_c = mcmc_samples["pm_c"] pm_d = mcmc_samples["pm_d"] |
以下のコードで事後分布を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 可視化 sns.set(style="darkgrid") plt.figure(figsize=(16, 8)) plt.subplot(2, 2, 1) sns.distplot(pm_a) plt.title("Probability Density of pm_a"); plt.subplot(2, 2, 2) sns.distplot(pm_b) plt.title("Probability Density of pm_b"); plt.subplot(2, 2, 3) sns.distplot(pm_c) plt.title("Probability Density of pm_c"); plt.subplot(2, 2, 4) sns.distplot(pm_d) plt.title("Probability Density of pm_d"); plt.show(); |

推論❶
num_samples=500でMCMCを実行したので、各パラメータ(pm_aなど)のサンプルが500個あります。そのうち100個のパラメータを採用し、x=0~1.0 のときの y を予測します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
X_range = np.linspace(0, 1, 10) N = 100 # 予測結果の可視化 fig = plt.figure(figsize=(6.0, 6.0)) for i in range(N): pm_y = [pm_c[i] * torch.sigmoid(-1.0 * (pm_a[i] * x + pm_b[i])) + pm_d[i] for x in X_range] plt.plot(X_range, pm_y, 'g-', alpha=0.3) # データセットの可視化 plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.title('sigmoid regression') plt.show() |
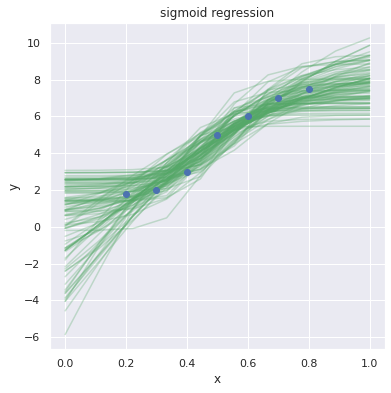
ベイズ推定では、予測に対する不確実性(uncertainty)を表現できる点が魅力の一つです。
推論❷
Predictiveを使って推論するコードが以下です。
|
1 2 3 4 5 6 7 8 9 |
X_range = np.linspace(0, 1, 10) Xt_range = torch.tensor(X_range) predictive = Predictive(model, mcmc_samples) predict_samples = predictive(X=Xt_range, Y=None) # print(predict_samples) pm_Y = predict_samples['pm_Y'] # print(pm_Y) |
以下のコードで予測結果を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 |
mean_Y = pm_Y.mean(axis=0) y_low, y_high = np.percentile(pm_Y, [2.5, 97.5], axis=0) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X_range, mean_Y, '-', color='g') plt.fill_between(X_range, y_low, y_high, color='g', alpha=0.3) plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.title('sigmoid regression') plt.show() |
 上図の予測結果を見る限り、良いモデリングができたと感じています。
上図の予測結果を見る限り、良いモデリングができたと感じています。
以上 Pyroによるベイズ統計モデリング実践でした。
まとめ
ベイズ統計モデリングについて勉強し『Pyroによる一般化線形モデル(GLM)のベイズモデル化』にトライした内容をまとめました。
本記事の内容について間違っている箇所やアドバイスなどあれば、教えて頂けると嬉しいです。
まだまだ勉強中ですが、ベイズ統計モデリングの理解が深まり楽しくなってきました!今後も勉強した内容を記事にしたいと思います。
本記事の前半で紹介したオススメの本を改めて紹介します。