こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
今回はガウス混合モデル(GMM:Gaussian Mixture Model)について勉強したので、備忘録も兼ねて本記事を書きます。
Contents
GMMとは
あるデータが複数のガウス分布から発生していると考えたとき、GMMにより各ガウス分布の平均・分散を予測することができます。
また各データが、どのガウス分布から発生したかも予測できるため、クラスタリングにも活用できます。
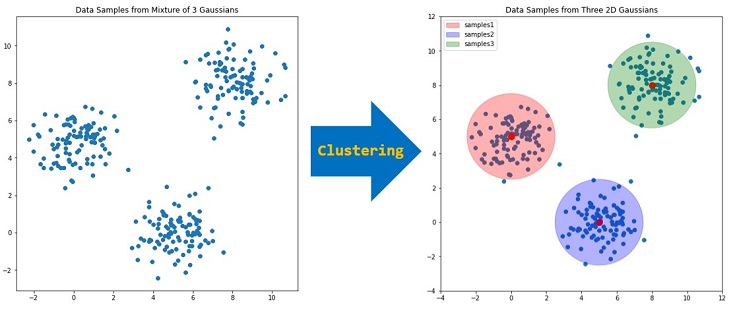
例えば上図は、クラスタ数が3のときのGMMによる推論のイメージです。
混合モデル(GMM含む)について、もっと勉強したい人のために、本記事の最後でオススメの本を紹介します
実践!Pyroでガウス混合モデル(GMM)をつくる
sklearnを活用することで、簡単にGMMによる推論を実現できますが、今回はPyroでゼロからガウス混合モデルをつくってみます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 |
import numpy as np import matplotlib.pyplot as plt from matplotlib.patches import Ellipse import torch import pyro import pyro.distributions as dist from pyro.infer.mcmc.api import MCMC from pyro.infer.mcmc import NUTS |
サンプルデータ作成
GMMの説明とは逆の手続きで、サンプルデータを作成します(下図参照)。
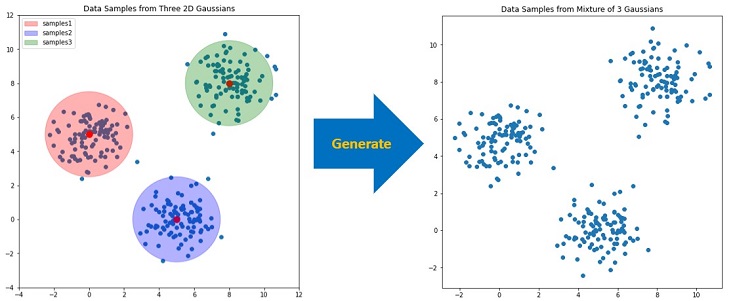
つまり3つのガウス分布からサンプルを生成し、そのサンプルを結合したデータを作成します。
Pyroを活用すれば、簡単に任意の確率分布からサンプルを生成することができます。今回の場合、以下のコードを使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
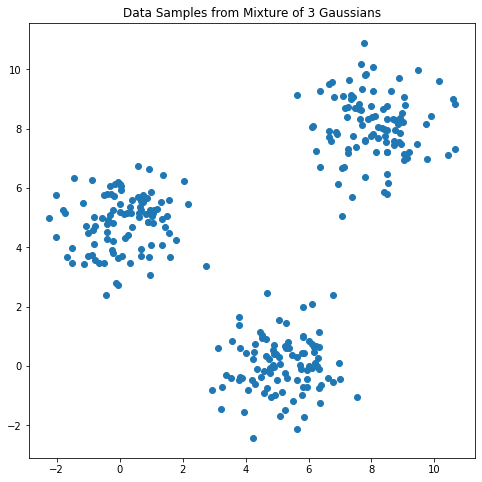
num_samples = 100 # mu and sigma of 2D gaussians mu1 = torch.tensor([0.0, 5.0]) sigma1 = torch.eye(2) mu2 = torch.tensor([5.0, 0.0]) sigma2 = torch.eye(2) mu3 = torch.tensor([8.0, 8.0]) sigma3 = torch.eye(2) # generate samples form 2D gaussians with pyro.plate('samples', num_samples): samples1 = pyro.sample('samples1', dist.MultivariateNormal(mu1, sigma1)) samples2 = pyro.sample('samples2', dist.MultivariateNormal(mu2, sigma2)) samples3 = pyro.sample('samples3', dist.MultivariateNormal(mu3, sigma3)) # generate data from concatenates samples data = torch.cat([samples1, samples2, samples3]) # visualize x = data[:, 0] y = data[:, 1] plt.figure(figsize=(8, 8)) plt.scatter(x, y); plt.title("Data Samples from Mixture of 3 Gaussians"); |
ベイズ統計モデリング
今回は以下のモデルを設計します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
K = 3 # number of components def model(data): ''' Gaussian Mixture Model''' weights = pyro.sample('weights', dist.Dirichlet(torch.ones(K))) scales = torch.eye(2) with pyro.plate('components', K): locs = pyro.sample('locs', dist.MultivariateNormal(torch.zeros(2), torch.eye(2, 2))) with pyro.plate('data', len(data)): z = pyro.sample('z', dist.Categorical(weights)) obs = pyro.sample('obs', dist.MultivariateNormal(locs[z], scales), obs=data) return obs, z |
モデルの概要は以下の通りです。
- K個の2次元ガウス分布から平均値(locs)を生成(※1)
- 共分散行列(scales)は単位行列で決め打ち(※2)
- ディリクレ分布とカテゴリ分布の組み合せで、データ割り当て(クラスタ z = 0 or 1 or 2)
- 各データが2次元ガウス分布(μ=locs[z], σ=scales)に従って発生(クラスタごとに μ と σ が存在する)
(※1) 2次元ガウス分布なので、円の中心=平均値=[x, y]
(※2) 分散を固定しているが、何らかの確率分布から発生させても良い
今回はシンプルに2次元ガウス分布の平均値(円の中心)のみを推論し、分散(円の大きさ)については、単位行列(単位円)で決め打ちします。
MCMC実行
以下のコードでMCMCによる推論を実行します。
|
1 2 3 4 |
pyro.set_rng_seed(2) kernel = NUTS(model) mcmc = MCMC(kernel, num_samples=100, warmup_steps=50) mcmc.run(data) |
推論結果の可視化
以下のコードでMCMCで算出された各パラメータを取得できます。
|
1 2 3 4 5 6 7 8 9 |
# get mcmc samples (num_samples=100) mcmc_samples = mcmc.get_samples() weights = mcmc_samples['weights'] locs = mcmc_samples['locs'] # print(mcmc_samples) # print(weights) # print(locs) |
以下のコードでクラスタごとの平均値を抽出し、さらに平均化したものを各2次元ガウス分布の平均値(円の中心)とします。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# クラスタごとの平均値 locs0 = locs[:, 0] locs1 = locs[:, 1] locs2 = locs[:, 2] # 2次元ガウス分布の平均値 loc0_x = locs0[:, 0].mean() loc0_y = locs0[:, 1].mean() loc1_x = locs1[:, 0].mean() loc1_y = locs1[:, 1].mean() loc2_x = locs2[:, 0].mean() loc2_y = locs2[:, 1].mean() |
以下のコードで推論結果を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 可視化 plt.figure(figsize=(14, 14)) plt.subplot(2, 2, 1) plt.scatter(data[:, 0], data[:, 1]); plt.scatter(locs0[:, 0], locs0[:, 1], color="red"); plt.scatter(locs1[:, 0], locs1[:, 1], color="red"); plt.scatter(locs2[:, 0], locs2[:, 1], color="red"); plt.title("locs"); plt.subplot(2, 2, 2) plt.scatter(data[:, 0], data[:, 1]); plt.scatter(loc0_x, loc0_y, s=99, color="red"); plt.scatter(loc1_x, loc1_y, s=99, color="red"); plt.scatter(loc2_x, loc2_y, s=99, color="red"); plt.title("loc"); |
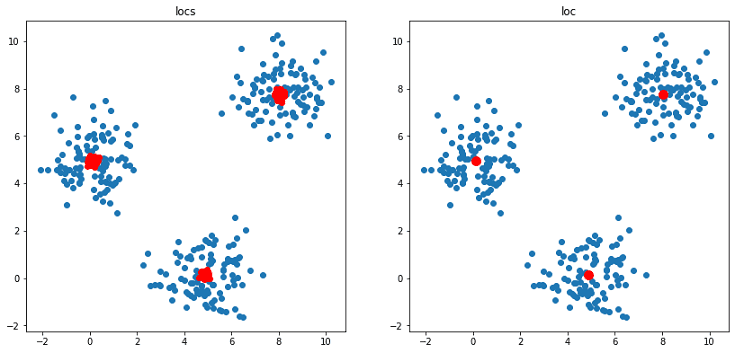
MCMC実行で num_samples=100 と設定したので、上図(左)の赤プロット(平均値)は100×3個ありますが、平均化することで上図(右)のように1点に絞り込みました。
平均値の真値と推論結果を比較したものが以下です。
| 真値:平均値(x, y) | 推論結果:平均値(x, y) | |
| Sample1 | (0, 5) | (0.0230, 4.9318) |
| Sample2 | (5, 0) | (4.8584, 0.1352) |
| Sample3 | (8, 8) | (7.8621, 7.9924) |
綺麗に予測できました。
まとめ
確率的プログラミング言語のPyroを活用し、ガウス混合モデル(GMM)を自作しました。
sklearnなどのライブラリを使えば、簡単にGMMを活用できますが『ゼロからモデリング』することで理解が深まったと感じています。
本記事の内容について間違っている箇所やアドバイスなどあれば、教えて頂けると嬉しいです。
以下 オススメの本と関連記事の紹介