こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。仕事でもプライベートでも機械学習で色々やってます。
先日 scikit-learn 0.23 がリリースされ、魅力的な機能が増えました。
今回は追加された機能の一つ、一般化線形モデル(GLM:Generalized Linear Model)を試してみます。
Contents
一般化線形モデル(GLM:Generalized Linear Model)とは
一般化線形モデル(GLM)については、以下の記事で丁寧に解説しているので、本記事では実践のみをします。
実践!scikit-learnで一般化線形モデル(GLM)
この記事と同じタスク「会計総額からチップ額を予測」に一般化線形モデル(GLM)を使います。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 |
import numpy as np import seaborn as sns import matplotlib.pyplot as plt import pandas as pd from sklearn.model_selection import train_test_split from sklearn.linear_model import PoissonRegressor from sklearn.linear_model import TweedieRegressor |
データ可視化
データセットをダウンロードして、データを可視化します。
|
1 2 3 4 5 6 7 8 9 10 |
# チップのデータセット df = sns.load_dataset("tips") # 会計総額とチップのデータを可視化 sns.set(style="darkgrid") sns.jointplot(x="total_bill", y="tip", data=df, kind="scatter", xlim=(0, 60), ylim=(0, 12), color="b", height=7); |
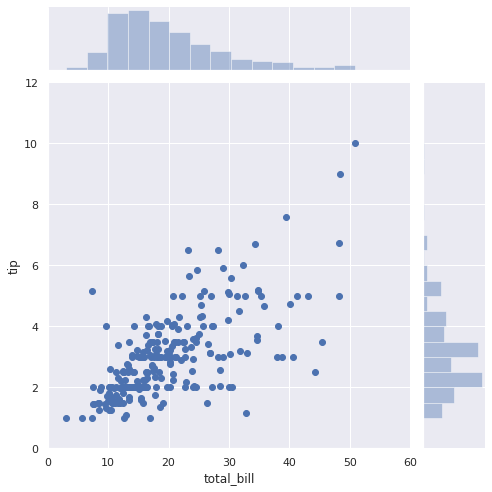
データの型変換と分割
扱えるデータの型に合わせて変換します。あとでスコア確認できるように、データ分割もしておきます。
|
1 2 3 4 5 6 7 8 9 |
# dfからnumpy.ndarrayに変換 y = df['tip'].values # 目的変数:y = [y0, y1, y2, ... yi] X = df['total_bill'].values # 説明変数:x = [x0, x1, x2, ... xi] # [x0, x1, x2,..] から [[x0], [x1], [x2]] に変換 X = X.reshape(len(X),1) # データ分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) |
今回は説明変数に会計総額(total_bill)の1つしか使いませんが、説明変数が複数ある場合、例えば説明変数が3つある場合は以下のような型変換が必要です。
X = [[1, 2, 3], [2, 3, 4], [3, 4, 5]]
統計モデリング
タスクが回帰、かつ確率分布:ポアソン分布、リンク関数:対数リンク関数を採用する場合、PoissonRegressor を使います。
|
1 2 3 4 5 6 7 8 |
# glm = PoissonRegressor() # デフォルト glm = PoissonRegressor( alpha=0, # ペナルティ項 fit_intercept=False, # 切片 max_iter=300, # ソルバーの試行回数 ) glm.fit(X_train, y_train) print("score:", glm.score(X_test, y_test)) |
モデルの良し悪しは置いといて、この記事と同じモデルを設計するため、デフォルトではなく上記のパラメータを採用しました。
あとはfitで推論(機械学習でいう学習)をすればOKです。scoreも簡単に算出できます。
予測結果の可視化
設計したモデルを使って予測をしてみます。
|
1 2 3 4 5 6 7 8 9 10 |
y_hat = glm.predict(X) # print(y_hat) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X, y, "o") plt.plot(X, y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |
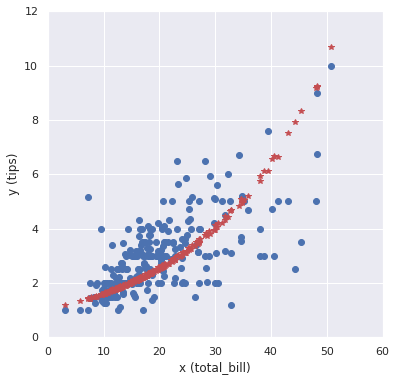
簡単にポアソン回帰ができました。
実践!scikit-learnで統計モデリング
TweedieRegressorを使えば、もっと柔軟な統計モデリングができます。
ポアソン回帰モデル
例えば、確率分布やリンク関数を任意に変更できます。
|
1 2 3 4 5 6 7 8 9 10 |
reg = TweedieRegressor( alpha=0, # ペナルティ項 power=1, # Poisson distribution link='log', # link function fit_intercept=False, # 切片 max_iter=300, # ソルバーの試行回数 ) reg.fit(X_train, y_train) print("score:", reg.score(X_test, y_test)) |
上記のようにすれば、先程と同じ確率分布:ポアソン分布、リンク関数:対数リンク関数を採用できます。
予測結果を可視化すると以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 |
y_hat = reg.predict(X) # print(y_hat) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X, y, "o") plt.plot(X, y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |

PoissonRegressor を使ったときと同じ結果が得られます。
線形回帰モデル
確率分布:正規分布、リンク関数:恒等リンク関数にすれば、線形回帰モデルを設計できます。
|
1 2 3 4 5 6 7 8 9 10 |
reg = TweedieRegressor( alpha=0, # ペナルティ項 power=0, # Normal distribution link='identity', # link function fit_intercept=False, # 切片 max_iter=300, # ソルバーの試行回数 ) reg.fit(X_train, y_train) print("score:", reg.score(X_test, y_test)) |
予測結果を可視化すると以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 |
y_hat = reg.predict(X) # print(y_hat) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X, y, "o") plt.plot(X, y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |
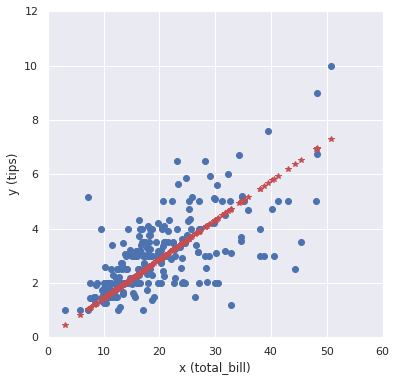
2020/05/15時点 TweedieRegressor がサポートしている確率分布は以下の通りです。
| Power | Distribution |
| 0 | Normal |
| 1 | Poisson |
| (1,2) | Compound Poisson Gamma |
| 2 | Gamma |
| 3 | Inverse Gaussian |
リンク関数は本記事でも採用した ‘identity‘ と ‘log’ をサポートしています。
今後のアップデートでサポートが充実してくると嬉しいですね。
まとめ
scikit-learnが一般化線形モデル(GLM)をサポートしたので、さっそく使ってみましたが、さすがscikit-learnです。とても簡単に統計モデリングができました。
一方で…
と思う人がいれば少し心配です。統計モデリングは奥が深いので、ちゃんと理解した上で使うのが理想的だと考えています。

微力ながら本ブログで「統計モデリング入門」の記事を公開していますので、良ければ参考にしてください。
以下の本で勉強してます。どれも素晴らしい本です。


























