こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
今回は確率的プログラミング言語のNumPyroによるベイズ統計モデリングに挑戦したので、備忘録も兼ねて本記事を書きます。
Contents
本記事で説明しないこと
本記事ではベイズ統計に関する理論や数式の説明はしません。用語については以下の記事で簡単に紹介していますが…
以下の本で勉強するのがオススメです。
以降から確率的プログラミング言語の概要を説明したあと、NumPyroによる統計モデリングについて、ソースコード付きで紹介します。
確率的プログラミング言語(PPL:Probabilistic Programming Language)とは
深層学習フレームワーク(TensorFlow, PyTorchなど)を活用することで、比較的簡単に深層学習モデルの設計ができるようになり、ディープラーニングの民主化が進みました。
ベイズ統計の分野でも確率的プログラミング言語(PPL:Probabilistic Programming Language)の登場により、モデリング作業の簡素化が整備されつつあります。
そのためディープラーニング同様に、ベイズ統計モデリングの民主化が進むと考えています。
代表的なPPL
PPL(Python用)の有名どころは以下の通りです。
PPLについて、もっと知りたい人のために、以下のスライドショーをオススメしておきます。
NumPyroとは
『Pythonで作って学ぶ統計モデリング』の記事に感化され、PyMC3を使っていましたが、MCMCの処理が遅くて少し不満でした。
そんなとき NumPyroのMCMC実行が高速という情報をキャッチしました。
※いずれも HELLO CYBERNETICS さんの記事です。いつもお世話になってます。
他にも以下の NumPyro 関連記事を見つけました。
NumPyro に興味を持ったので、触ってみることにしました。
実践!NumPyroでベイズ回帰モデルをつくる -その1-
以下の記事と同じ問題設定「会計総額からチップ額を予測」にベイズ回帰モデルを活用します。

なお本記事のソースコードはGoogle Colabで動作確認しました。
インストール
最初に以下のコマンドでNumPyroをインストールします。
pip install numpyro
以降からコード書いていきます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 9 10 11 |
import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import jax.numpy as jnp from jax import random, vmap, grad, jit, lax import numpyro from numpyro import plate, sample from numpyro.infer import MCMC, NUTS, Predictive import numpyro.distributions as dist |
データ可視化
データセットをロードして、データを可視化します。
|
1 2 3 4 5 6 7 8 9 10 |
# チップのデータセット df = sns.load_dataset("tips") # 会計総額とチップのデータを可視化 sns.set(style="darkgrid") sns.jointplot(x="total_bill", y="tip", data=df, kind="scatter", xlim=(0, 60), ylim=(0, 12), color="b", height=7); |
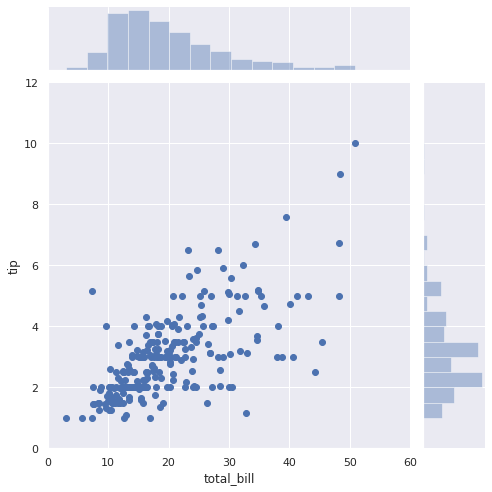
説明変数と目的変数
説明変数:X と 目的変数:Y を定義します。
|
1 2 3 |
# dfからnumpy.ndarrayに変換 Y = df['tip'].values # 目的変数:Y = [y0, y1, y2, ... yi] X = df['total_bill'].values # 説明変数:X = [x0, x1, x2, ... xi] |
ベイズ統計モデリング -線形回帰モデル-
今回は X から Y を予測するモデルを以下のように設計しました。
【線形回帰モデル】
y = ax + b
【事前分布】
pm_a ~ Normal(μ=0.0, σ=10.0)
pm_b ~ Normal(μ=0.0, σ=10.0)
【確率モデル】
pm_Y ~ Normal(μ=y, σ=1.0)
ここでは a を傾き、b を切片と呼ぶことにし、y = ax + b で”あてはまり”の良い予測ができると考えました。
また傾き:a、切片:b、予測値:y が正規分布に従うと考えました。
上記のモデルをNumPyroで実装したものが以下です。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 線形回帰モデルの設計 def model(X, Y=None): pm_a = numpyro.sample('pm_a', dist.Normal(0.0, 10.0)) pm_b = numpyro.sample('pm_b', dist.Normal(0.0, 10.0)) mu = pm_a * X + pm_b sigma = 1.0 pm_Y = numpyro.sample('pm_Y', dist.Normal(mu, sigma), obs=Y) return pm_Y |
MCMCの実行
以下のコードでMCMCの実行と pm_a や pm_b の基本統計量を確認できます。
|
1 2 3 4 5 6 7 |
# Run MCMC kernel = NUTS(model) mcmc = MCMC(kernel, num_warmup=1000, num_samples=2000) mcmc.run(rng_key=random.PRNGKey(0), X=X, Y=Y) # print MCMC summary(推定パラメータの基本統計量) mcmc.print_summary() |
| mean | std | median | 5.0% | 95.0% | n_eff | r_hat | |
| pm_a | 0.11 | 0.01 | 0.11 | 0.09 | 0.12 | 379.86 | 1.00 |
| pm_b | 0.92 | 0.16 | 0.92 | 0.64 | 1.17 | 362.92 | 1.00 |
※num_samples=2000なので、pm_a と pm_b のサンプル数が2,000あります
事後分布の可視化
MCMCで算出された推定パラメータ(pm_a、pm_b)は以下のコードで取得できます。
|
1 2 3 4 5 6 7 8 |
# get param (num_samples=2000) mcmc_samples = mcmc.get_samples() pm_a = mcmc_samples["pm_a"] pm_b = mcmc_samples["pm_b"] # print("mcmc_samples:", mcmc_samples) # print("pm_a:", pm_a) # print("pm_b:", pm_b) |
pm_a および pm_b は 事後分布なので、以下のコードで分布を可視化できます。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 可視化 sns.set(style="darkgrid") plt.figure(figsize=(15, 5)) plt.subplot(1, 2, 1) sns.distplot(pm_a) plt.title("Probability Density of pm_a") plt.subplot(1, 2, 2) sns.distplot(pm_b) plt.title("Probability Density of pm_b") plt.show() |
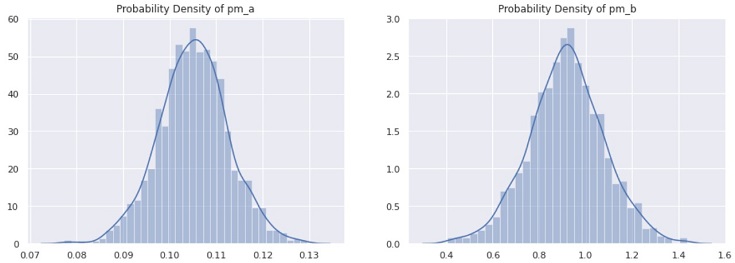
推論
以下のコードで X=0, 1, …, 49, 50 のときの Y を予測します。
|
1 2 3 4 5 6 7 8 |
X_range = jnp.linspace(0, 50, 50) predictive = Predictive(model, mcmc_samples) predict_samples = predictive(random.PRNGKey(0), X=X_range, Y=None) # print(predict_samples) pm_Y = predict_samples['pm_Y'] print(pm_Y) |
以下のコードで予測結果を可視化します。
|
1 2 3 4 5 6 7 8 9 10 |
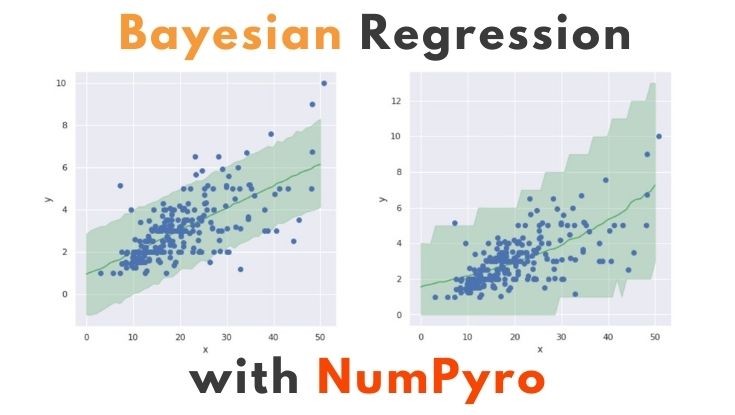
mean_Y = pm_Y.mean(axis=0) y_low, y_high = jnp.percentile(pm_Y, [2.5, 97.5], axis=0) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X_range, mean_Y, '-', color='g') plt.fill_between(X_range, y_low, y_high, color='g', alpha=0.3) plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.show() |
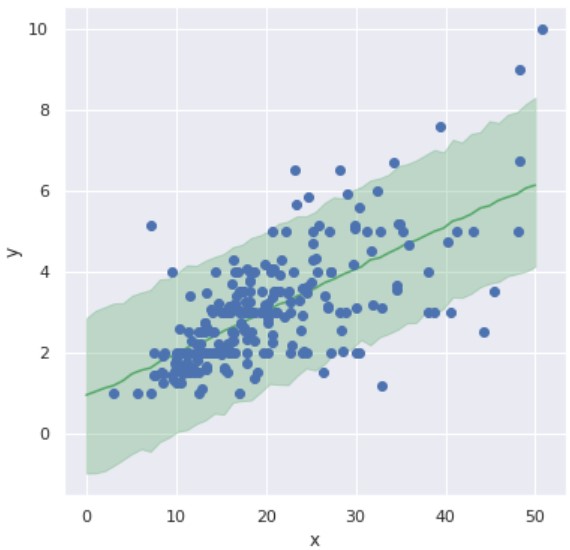
ベイズ回帰モデルでは、予測に対する不確実性(uncertainty)を表現できる点も魅力の一つです。
つまり『任意の x に対する予測値 y を一意に決めず、上図の緑の範囲に予測値 y が含まれる』という表現ができます。
全ての推定パラメータを使って推論・可視化
推定パラメータ:pm_a, pm_b の全サンプル(今回は2,000サンプル)で推論します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
N = len(pm_a) # X_range = jnp.linspace(0, 50, 50) # 予測結果の可視化 fig = plt.figure(figsize=(6.0, 6.0)) for i in range(N): pm_y = [pm_a[i] * x + pm_b[i] for x in X_range] plt.plot(X_range, pm_y, 'g-', alpha=0.5) # データセットの可視化 plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.title('linear regression') plt.show() |
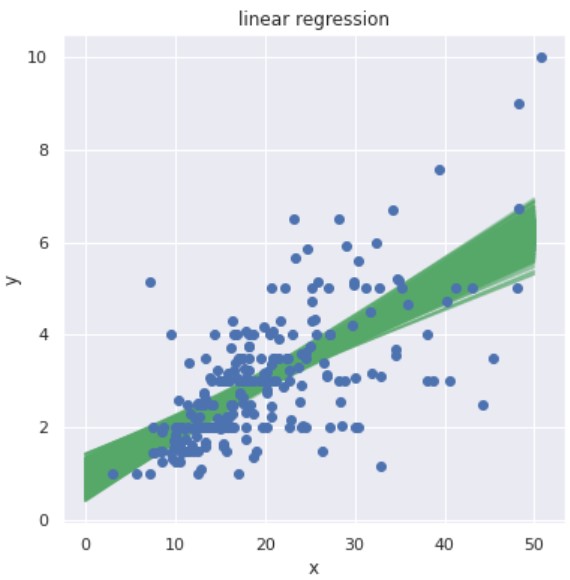
これも予測に対する不確実性を表現しており、線の数だけ予測候補があることを示しています。
線形回帰モデル
最後に pm_a, pm_b の平均値を採用して、線形回帰モデルをつくります(扱いやすいように関数化しておきます)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def my_model(mcmc_samples, X): '''線形回帰モデル''' mcmc_samples = mcmc.get_samples() pm_a = mcmc_samples["pm_a"] pm_b = mcmc_samples["pm_b"] # 平均値 mu_a = jnp.mean(pm_a, axis=0) mu_b = jnp.mean(pm_b, axis=0) print("mu_a=", mu_a) print("mu_b=", mu_b) # 線形回帰モデル Y_hat = mu_a * X + mu_b return Y_hat |
以下のコードでmy_model()による推論および結果の可視化をします。
|
1 2 3 4 5 6 7 8 9 10 |
# 予測値 Y_hat = my_model(mcmc_samples, X) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X, Y, "o") plt.plot(X, Y_hat, "g-") plt.xlabel('x'), plt.ylabel('y') plt.title('linear regression') plt.show() |
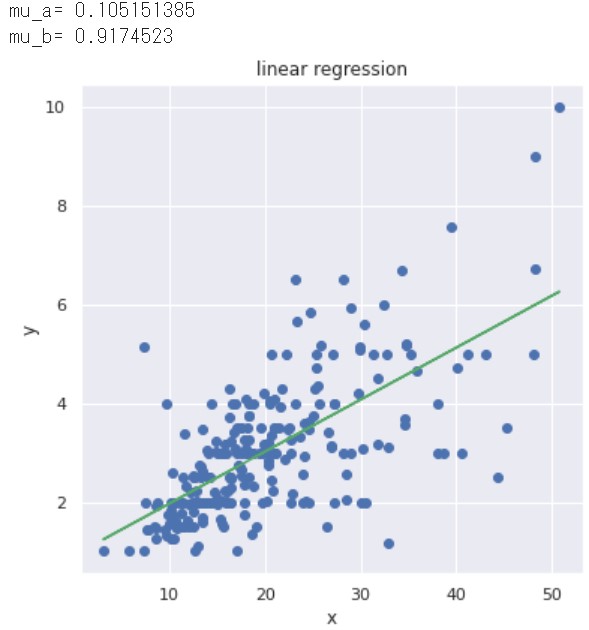
こうすることで『任意の x に対する予測値 y を一意に決めるモデルを生成』できるため、システムなどに組み込み易くなります。
以上までが【NumPyroでベイズ回帰モデルをつくる -その1-】でした。もう一つベイズ統計モデリングの例を紹介します。
実践!NumPyroでベイズ回帰モデルをつくる -その2-
【その1】と同じ問題設定で、モデルのみを変更します。
ベイズ統計モデリング -ポアソン回帰モデル-
今度は以下のようなモデルを設計しました。
【ポアソン回帰モデル】
y = exp(ax + b)
【事前分布】
pm_a ~Normal(μ=0.0, σ=10.0)
pm_b ~ Normal(μ=0.0, σ=10.0)
【確率モデル】
pm_Y ~ Poisson(μ=Y)
【その1】との違いは y = exp(a*x + b) を採用し、かつポアソン分布に従うと考えた点です。
上記のモデルをNumPyroで実装したものが以下です。
|
1 2 3 4 5 6 7 8 9 |
# ポアソン回帰モデルの設計 def model(X, Y=None): pm_a = numpyro.sample('pm_a', dist.Normal(0.0, 10.0)) pm_b = numpyro.sample('pm_b', dist.Normal(0.0, 10.0)) theta = pm_a * X + pm_b mu = jnp.exp(theta) numpyro.sample('pm_Y', dist.Poisson(mu), obs=Y) |
MCMCの実行
あとは【その1】と同じで、MCMCを実行します。
|
1 2 3 4 5 6 7 8 |
# Run MCMC kernel = NUTS(model) # mcmc = MCMC(kernel, num_warmup=1000, num_samples=2000, num_chains=4) mcmc = MCMC(kernel, num_warmup=1000, num_samples=2000) mcmc.run(rng_key=random.PRNGKey(0), X=X, Y=Y) # print MCMC summary(事後分布の基本統計量を確認) mcmc.print_summary() |
| mean | std | median | 5.0% | 95.0% | n_eff | r_hat | |
| pm_a | 0.03 | 0.00 | 0.03 | 0.02 | 0.04 | 429.94 | 1.00 |
| pm_b | 0.46 | 0.10 | 0.46 | 0.31 | 0.62 | 400.91 | 1.00 |
コード割愛しますが、事後分布を可視化したものが下図です。
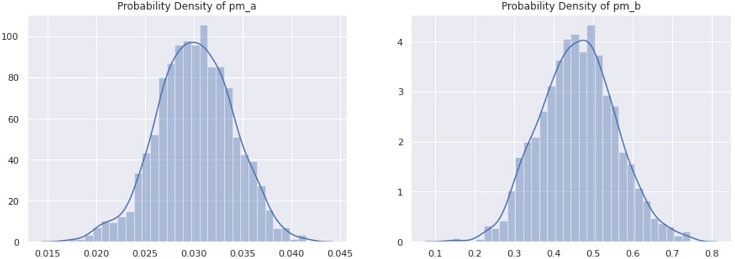
推論
以下のコードで X=0, 1, …, 49, 50 のときの Y を予測します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
X_range = jnp.linspace(0, 50, 50) predictive = Predictive(model, mcmc_samples) predict_samples = predictive(random.PRNGKey(0), X=X_range, Y=None) # print(predict_samples) pm_Y = predict_samples['pm_Y'] # print(pm_Y) mean_Y = pm_Y.mean(axis=0) y_low, y_high = jnp.percentile(pm_Y, [2.5, 97.5], axis=0) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X_range, mean_Y, '-', color='g') plt.fill_between(X_range, y_low, y_high, color='g', alpha=0.3) plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.show() |
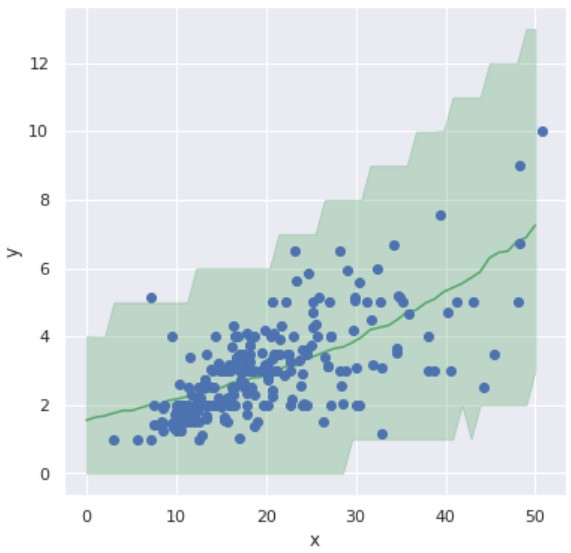
【その1】同様、予測に対する不確実性(uncertainty)を表現できています。
全ての推定パラメータを使って推論・可視化
推定パラメータ:pm_a, pm_b の全サンプル(今回は2,000サンプル)で推論します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
N = len(pm_a) # X_range = jnp.linspace(0, 50, 50) # 予測結果の可視化 fig = plt.figure(figsize=(6.0, 6.0)) for i in range(N): pm_y = [jnp.exp(pm_a[i] * x + pm_b[i]) for x in X_range] plt.plot(X_range, pm_y, 'g-', alpha=0.5) # データセットの可視化 plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.title('linear regression') plt.show() |
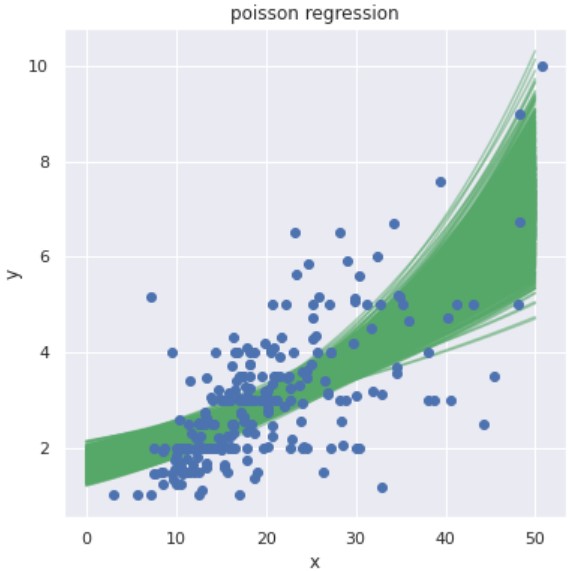
※ x:会計総額(total_bill), y:チップ額(tip)
xの値が大きいほど、yの予測候補の範囲が広いことが分かります。この予測範囲の広さを「予測結果の自信の無さ」という解釈ができそうです。
例えば、会計総額が小さい場合、チップ額(予測値)の”ばらつき”が小さいです。これを直観的に解釈すると「会計総額が小さい場合、ある程度”決まりきったチップ額”になる」といえそうです。
一方で会計総額が大きくなるにつれて、チップ額(予測値)の”ばらつき”も大きくなります。これは「会計総額が大きい客の中に、気前の良い客が含まれており、線形増加ではないチップ額を支払う場合もある」といえそうです。
ただし、会計総額が大きいときのサンプルが少ないので、モデルは自信のある予測ができない…などの解釈ができそうです。
ポアソン回帰モデル
最後にpm_a, pm_bの平均値を採用して、ポアソン回帰モデル(の関数)をつくり、結果の可視化まで行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
def my_model(mcmc_samples, X): '''ポアソン回帰モデル''' mcmc_samples = mcmc.get_samples() pm_a = mcmc_samples["pm_a"] pm_b = mcmc_samples["pm_b"] # 平均値 mu_a = jnp.mean(pm_a, axis=0) mu_b = jnp.mean(pm_b, axis=0) print("mu_a=", mu_a) print("mu_b=", mu_b) # ポアソン回帰モデル Y_hat = jnp.exp(mu_a * X + mu_b) return Y_hat # 予測値 Y_hat = my_model(mcmc_samples, X_range) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X, Y, "o") plt.plot(X_range, Y_hat, "g-") plt.xlabel('x'), plt.ylabel('y') plt.title('poisson regression') plt.show() |
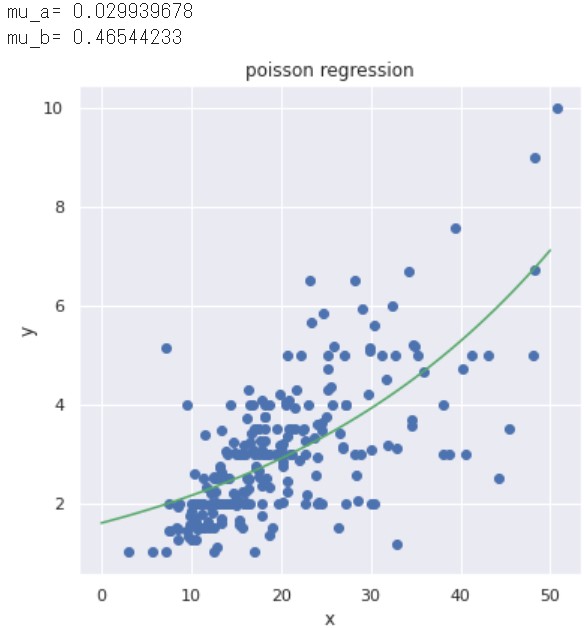
以上までが【NumPyroでベイズ回帰モデルをつくる -その2-】でした。
まとめ -ベイズ統計モデリング入門-
ベイズ統計モデリングについて勉強し、NumPyroによる実践までした内容をまとめました。
本記事の内容について間違っている箇所があれば、教えて頂けると嬉しいです。
ベイズ統計モデリングは難しいけど、強力な武器になると感じたので、今後も勉強した内容を記事にしたいと考えています。
以下 本記事の前半で紹介したオススメの書籍を改めて載せておきます。