こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。仕事でもプライベートでも機械学習で色々やってます。
今回は統計モデルの一つ、一般化線形モデル（GLM：Generalized Linear Model）について勉強したので、備忘録も兼ねて本記事を書きます。
Contents
統計モデリング入門
最初に「モデリング」や「モデル」などの用語について整理しておきます。
モデリングとは
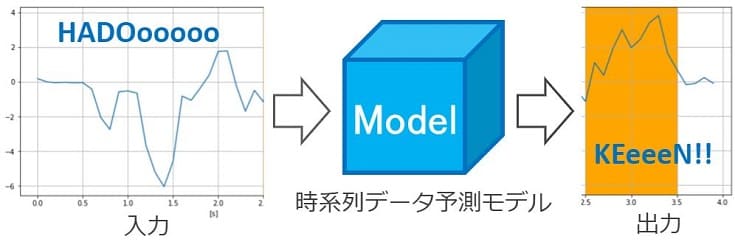
あるデータを入力したとき、ユーザーがほしい情報を出力する箱をモデルと呼びます。
例えば下図は、あるパターンの波形を入力すると、その数秒先の波形を予測（出力）するモデルのイメージです。
このモデルを設計する作業がモデリングです。具体的には、モデルの中身にあたるアルゴリズムを検討する作業のことです。
近年では深層学習モデルが人気です。実は上図もLSTMと呼ばれるアルゴリズムを活用した深層学習モデルです。
統計モデリングと統計モデル
統計モデリングとは、文字通り統計学をベースにしたモデルを設計することです。具体的にどんな統計モデル（アルゴリズム）があるかについては、以下の記事が非常に参考になります。
統計モデリングを学ぶモチベーション
下記の記事に書きましたが、タスクやクライアントに応じて、最適な手法（ニーズにフィットする手法）を検討する必要があります。
深層学習モデルはブラックボックスモデルなので、タスク次第では採用が困難です。
モデルの説明性・解釈性を明示できる統計モデルを活用すれば、解決できる課題が大幅に増えると考えています。
線形モデル（LM：Linear Model）とは
一般化線形モデル（GLM：Generalized Linear Model）より先に、線形モデル（LM：Linear Model）を例に統計モデリングの基礎を説明します。
問題設定（タスク）
入力値xから出力値yを予測するタスクを回帰（regression）と呼びます。例えば、下記のサンプルがあったとします。
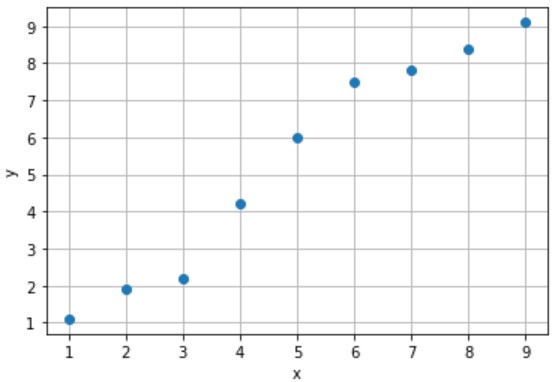
このサンプルを参考に、まだ収集できていない未知のデータx（例えば x=5.5 など）に対するデータyを予測するモデルを設計します。
モデリングとオーバーフィッティング
入力値xから赤線上の出力値yを予測するモデルAとモデルBを設計しました（下図参照）。
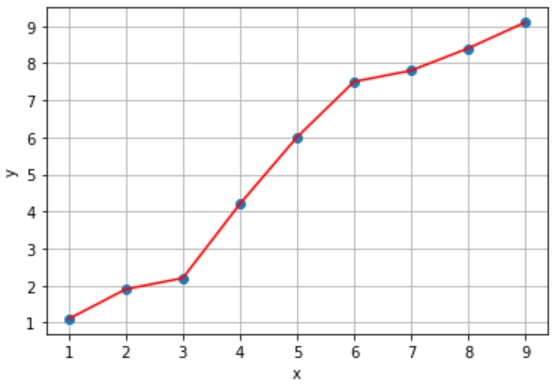
（例）x=5のときy=6と予測（誤差なし）
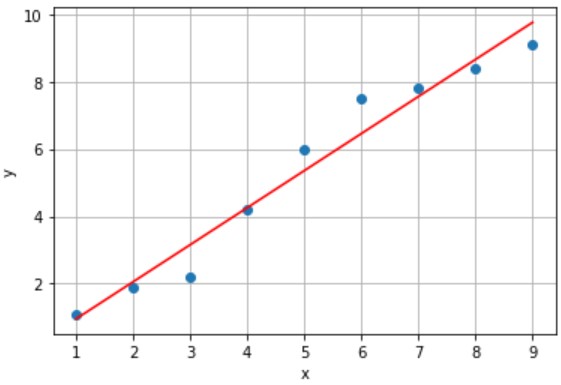
（例）x=5のときy=5.7と予測（誤差 0.3）
誤差のないモデルAの方が予測精度が良い気がします。しかし、未知のデータx（橙プロット）に対する予測はどうでしょう？
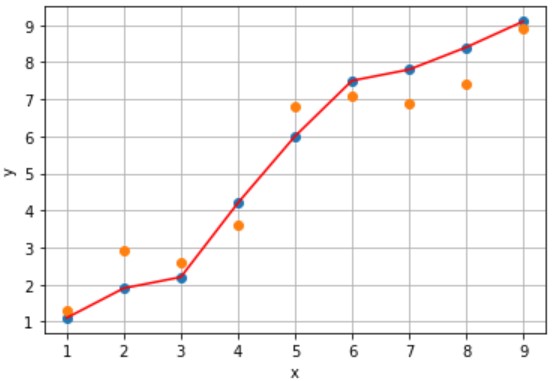
- 誤差：あり、累計誤差：大きい
- x=5.5のときy=6.8と予測
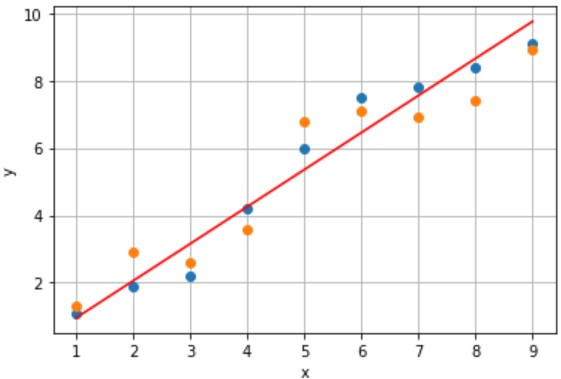
- 誤差：あり、累計誤差：小さい
- x=5.5のときy=6.0と予測
モデルAは収集できたサンプルにフィットし過ぎたモデルなので、未知のデータに対し、精度の良い予測ができません。
一方、モデルBは誤差が小さくなるように設計したモデルなので、未知のデータに対しても、累計誤差が小さくなります。
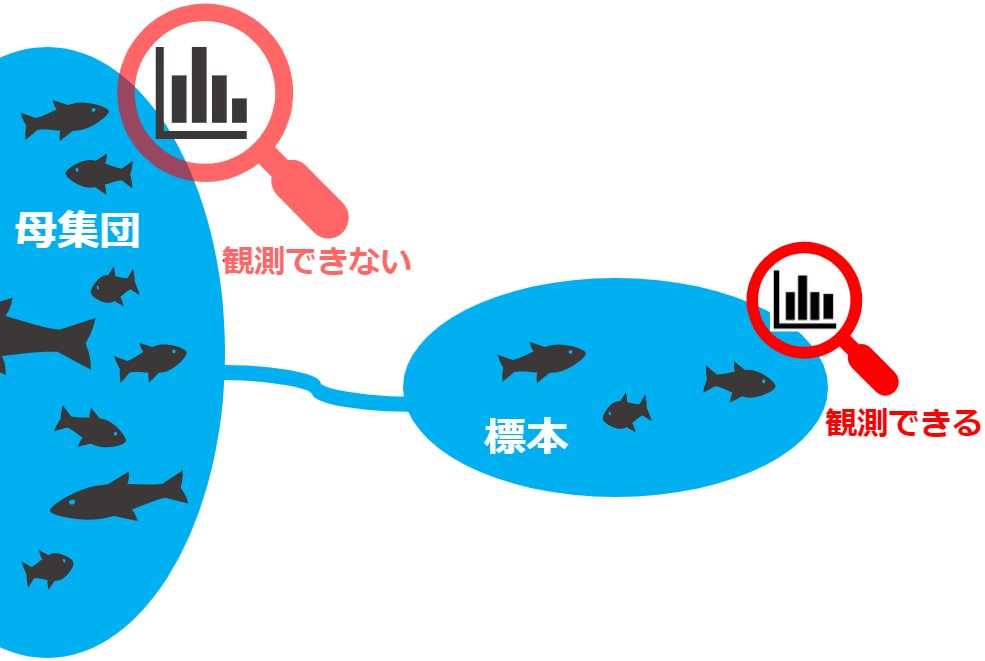
もっと具体的に言えば、今回のタスクが「ある地域に生息する魚の体重xから尾びれのサイズyを予測する」だったとます。
モデリングに使用したサンプルは、母集団から収集できた一部のデータに過ぎないため、そのサンプルにオーバーフィットするモデルはNGです（サンプルの中に”巨大な魚”が含まれていたら、オーバーフィットはNGですよね）。
言い換えれば、背後にある観測できないデータも考慮してモデリングすべきです（”巨大な魚”が外れ値であることを考慮すべきですね）。
統計モデリングでは、背後にあるデータ（真の確率分布）を考慮したモデルを設計します。
線形モデルと一般化線形モデルの関係
上記のモデルBのことを線形モデル（LM：Linear Model）、より正確には線形回帰モデル（linear regression model）と呼びます。
線形回帰モデルの中身（y = w0 + w1x）、つまり赤線の切片w0と傾きw1は最小二乗法で算出できます。
また、一般化線形モデルのキーワード「線形予測子」・「確率分布」・「リンク関数」を以下のようにモデリングしても算出できます。
- 線形予測子：w0 + w1x
- 確率分布：正規分布
- リンク関数：恒等関数 g(μ) = μ
順番に説明します。
一般化線形モデル（GLM：Generalized Linear Model）とは -理論編-
以降から 使える統計モデル10選（前編）や以下の本で紹介している一般化線形モデル（GLM：Generalized Linear Model）について徹底解説します。
一般化線形モデルの設計
大事なことなので繰り返しますが、観測できたサンプルのみからモデリングします。
ただし、サンプルにオーバーフィットしたモデルはNGです。背後にあるデータ（真の確率分布）を考慮したモデリングが重要です。
具体的には、一般化線形モデルの場合「線形予測子」・「確率分布」・「リンク関数」を検討する作業が重要です。
線形予測子
最初に、下記の理想的なモデルの右辺を検討します。
【理想的なモデル】
Y = ???
複数の要因Xiが出力Yに作用すると考え、以下のモデル設計します。
【一般化線形モデル（GLM）】
- 説明変数の数：k
- 重み（説明変数にかかるパラメータ）：wk
- 説明変数：Xk=[x0, x1, … ,xi]
- 目的変数：Y=[y0, y1, … ,yi]
- サンプル数：i
- オフセット項：ε
※本記事では オフセット項：ε の説明を割愛します
これが一般化線形モデル（GLM）です。そして、この式の右辺が「線形予測子」です。
例えば「ある地域に生息する魚の体重xから尾びれのサイズyを予測する」一般化線形モデルなら、以下の式になります。
【線形回帰モデル】
y = w0 + w1x
- 説明変数の数：1（自明ですがx1=x）
- 重み：線形回帰モデルの切片w0, 傾きw1
- 説明変数：x（魚の体重）
- 目的変数：y（尾びれのサイズ）
- サンプル数：i=1
- オフセット項：なし
※1入力1出力系
これ線形モデルですね。つまり、線形モデルは一般化線形モデルの一部ということです。
- 数式の変数（説明変数など）の大文字はベクトル、小文字は１変数
- 線形モデルは一般化線形モデルの一部
確率変数
続いて、観測できたサンプルから背後にあるデータの「確率分布」を推定します。
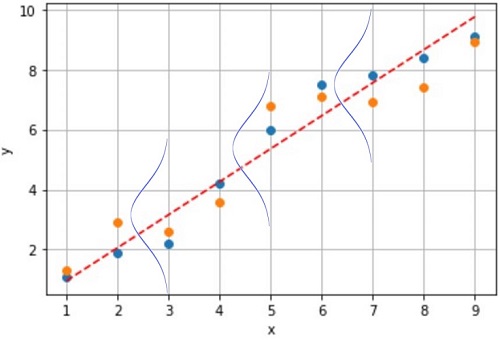今回はデータyの確率分布が「正規分布（ガウス分布）」だと”あてはまりが良い”と考えます。
【正規分布】
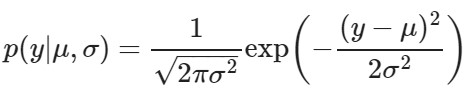
- データyは平均値 μ を中心にばらつく
- 分散 σ から ばらつき を推定できる
サンプル数が多いほど、真の確率分布を推定しやすいので、データ収集は重要な工程です。
- 観測できたサンプルから真の確率分布を推定する
- サンプル数が多いほど確率分布の推定はしやすい
- 真の確率分布が正規分布ではないときもある
リンク関数
データyが正規分布に従い、かつ線形回帰モデルで予測できるなら、以下の式で予測するのが最も期待値が高くなります。
【リンク関数】
y = μ
- データyは平均値 μ を中心にばらつく
- y=μのデータが最も多く収集できる
- y=μと予測するのが最も期待値が高くなる
この式を線形予想子とリンクさせたものが以下です。
【リンク関数と線形予測子】
μ = w0 + w1x
この式の右辺f(x)は線形予測子でした。この式の左辺g(μ)がリンク関数です。
【リンク関数】
g(μ) = μ
つまり、期待値μの関数がリンク関数です。今回の場合、リンク関数に恒等関数を採用しているので、恒等リンク関数と呼びます。
- 予測値yの期待値が最も大きくなる数式を考える
- データが正規分布に従い、かつ線形なら恒等リンク関数を採用する
- 恒等リンク関数以外を採用すべきデータもある
まとめ 一般化線形モデル -理論編-
改めて、設計したモデルを確認します。
g(μ) = w0 + w1x
- 線形予測子：w0 + w1x
- 確率分布：正規分布
- リンク関数：恒等関数 g(μ) = μ
あとは、このモデルの重みwiをコンピュータで算出すればOKです。
実践！統計モデリング基礎 -線形モデル編-
理論の説明はここまでにして、次はPythonライブラリ statsmodels で統計モデリングを実践してみます。
問題設定（タスク）：会計総額からチップ額を予測
海外ではレストランで食事をしたときに、チップを支払う習慣があるそうです。会計総額（total_bill）からチップ額（tip）を予測する統計モデルを設計します。
【使用するデータセット】
Import
まずはimportから
|
1 2 3 4 5 6 7 |
import numpy as np import statsmodels.api as sm import statsmodels.formula.api as smf import seaborn as sns import matplotlib.pyplot as plt import pandas as pd |
データセットの中身確認
データセットをダウンロードして中身を確認します。
|
1 2 3 |
# チップのデータセット df = sns.load_dataset("tips") df.head(3) |
| total_bill | tip | sex | smoker | day | time | size |
|---|---|---|---|---|---|---|
| 16.99 | 1.01 | Female | No | Sun | Dinner | 2 |
| 10.34 | 1.66 | Male | No | Sun | Dinner | 3 |
| 21.01 | 3.50 | Male | No | Sun | Dinner | 3 |
データ可視化
データ解析ではデータの可視化が重要です。
|
1 2 3 4 5 6 7 |
# 会計総額とチップのデータを可視化 sns.set(style="darkgrid") sns.jointplot(x="total_bill", y="tip", data=df, kind="scatter", xlim=(0, 60), ylim=(0, 12), color="b", height=7); |
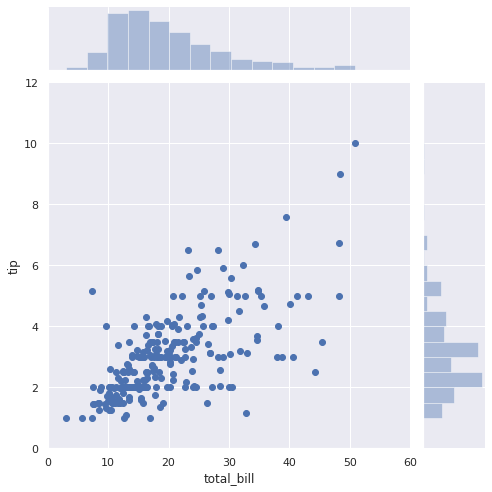
上図より、以下があてはまりが良いモデルだと考えました。
g(μ) = wx
- 線形予測子：wx
- 確率分布：正規分布
- リンク関数：恒等関数 g(μ) = μ
線形予測子・確率分布・リンク関数の推定
statsmodels公式がサポートしている 確率分布（family）・ リンク関数（link）を確認し、よく使われる組み合わせも Notes で確認します。
今回の設計は以下の通りです。
|
1 2 3 4 |
y = df['tip'] # 目的変数：y x = df['total_bill'] # 説明変数：x（線形予測子：wx） link = sm.families.links.identity() # リンク関数：恒等リンク関数 family = sm.families.Gaussian(link) # 確率分布：ガウス分布 |
推論
統計モデリングでは、真の確率分布にあてはまりの良いモデルを「推論」する工程が、機械学習モデリングでいう「学習」に相当します。
なので本記事では model.fit() を含む以下の処理を「学習」ではなく「推論」と呼びます。
|
1 2 3 4 |
# model model = sm.GLM(y, x, family=family) results = model.fit() print(results.summary()) |
設計したモデルはsummary()で確認できます（上図参照）。詳細説明は割愛しますが、説明変数x（total_bill） にかかる 重みが w=0.1437 と算出されました。
予測結果の可視化
設計したモデルを使って予測をしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 重み w = results.params[0] # 0.1437 # フィッティング直線 # y_hat = results.predict(x) y_hat = w * x # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(x, y, "o") plt.plot(x, y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |
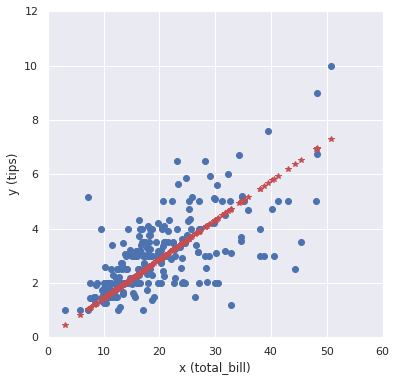
上図の赤プロットが予測結果です。なかなか良さそうなモデルですね。
seabornで線形回帰
実は seaborn でも線形回帰モデルを自動で算出して結果を描画できます。
|
1 2 |
sns.lmplot(x="total_bill", y="tip", data=df); plt.plot(x, y_hat, "*", color="r"); |
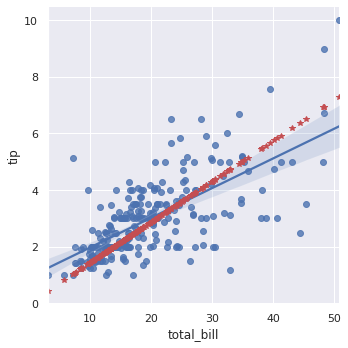
statsmodelsで設計したモデル（赤プロット）と seaborn のモデル（実線）で異なる結果になりました。これは seaborn のモデルに切片w0の項が存在するからです。
【線形モデル】
g(μ) = w0 + w1x
切片のあるモデル
statsmodelsでは sm.add_constant(x) とすれば、切片のあるモデルになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# model 切片あり model = sm.GLM(y, sm.add_constant(x), family=family) results = model.fit() print(results.summary()) # 重み w0 = results.params[0] # 0.9203 w1 = results.params[1] # 0.1050 # フィッティング直線 y_hat = w0 + w1 * x # y_hat = results.predict(x) # 可視化 sns.lmplot(x="total_bill", y="tip", data=df); plt.plot(x, y_hat, "*", color="r"); |
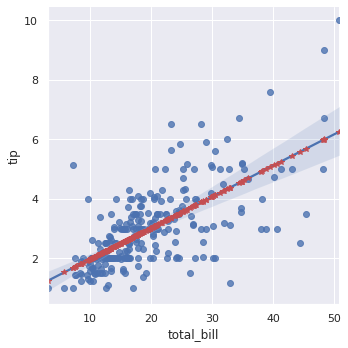
これで切片のあるモデルになりました。ただし、total_bill=0なのにtip≠0って不自然ですよね？
常識的に不自然なモデルになっていないか確認することが大事ですね
モデルの保存と読込み
納得のいくモデルができたら、以下のコードでモデルを保存しておきます。
|
1 2 3 |
results.save("./test.pkl") |
※パスは適当に変更してください
以下のコードで保存したモデルを読みこめます。
|
1 2 |
test_model = sm.load("./test.pkl") print(test_model.params) |
以上までがstatsmodelsを活用した「統計モデリング基礎」でした。以降で少しだけ応用について説明します。
実践！統計モデリング応用 -一般化線形モデル編-
線形予測子・確率分布・リンク関数を変更して統計モデリングしてみます。今回は喫煙/禁煙（smoker）の説明変数を追加し、予測結果（チップ額）が変化するか試してみます。
前処理
文字列は扱えないのでダミー変数に変換します。
|
1 2 3 4 5 6 7 8 9 10 |
# 元データをコピー df_dummy = df.copy() # ダミー変数に変更 df_dummy['sex'] = pd.get_dummies(df_dummy['sex']) # Female=0, male=1 df_dummy['time'] = pd.get_dummies(df_dummy['time']) # Dinner=0, Lunch=1 df_dummy['smoker'] = df_dummy['smoker'].map({'No': 0, 'Yes': 1}) # No=0, Yes=1 df_dummy['smoker'] = df_dummy['smoker'].astype('uint8') # dtype: category 変換 dtype: uint8 df_dummy.head(3) |
| total_bill | tip | sex | smoker | day | time | size |
|---|---|---|---|---|---|---|
| 16.99 | 1.01 | 0 | 0 | Sun | 0 | 2 |
| 10.34 | 1.66 | 1 | 0 | Sun | 0 | 3 |
| 21.01 | 3.50 | 1 | 0 | Sun | 0 | 3 |
※後から使いそうなsmoker以外の説明変数もダミー変数に変換
線形予測子を変更（説明変数を増やす）
説明変数が増えても使用するコードはほとんど同じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Yd = df_dummy['tip'] # 目的変数 Xd = df_dummy[['total_bill', 'smoker']] # 説明変数のx1とx2（線形予測子：w1x1 + w2x2） link = sm.families.links.identity() # 恒等リンク関数 family = sm.families.Gaussian(link) # ガウス分布 # model model = sm.GLM(Yd, Xd, family=family) results = model.fit() print(results.summary()) # 重み w1 = results.params[0] # 0.143077 w2 = results.params[1] # 0.038961 # フィッティング直線 y_hat = results.predict(Xd) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(Xd['total_bill'], Yd, "o") plt.plot(Xd['total_bill'], y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |
可視化やsummaryの結果は割愛しますので、手を動かして確認してみてください。
確率分布とリンク関数も変更
リンク関数を対数リンク関数に、確率分布をポアソン分布に変更します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Yd = df_dummy['tip'] Xd = df_dummy[['total_bill', 'smoker']] link = sm.families.links.log() # 対数リンク関数 family = sm.families.Poisson(link) # ポアソン分布 # model model = sm.GLM(Yd, Xd, family=family) results = model.fit() print(results.summary()) # フィッティング直線 y_hat = results.predict(Xd) # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(Xd['total_bill'], Yd, "o") plt.plot(Xd['total_bill'], y_hat, "*", color="r") plt.xlabel('x (total_bill)'), plt.ylabel('y (tips)') plt.xlim(0, 60), plt.ylim(0, 12) plt.show() |
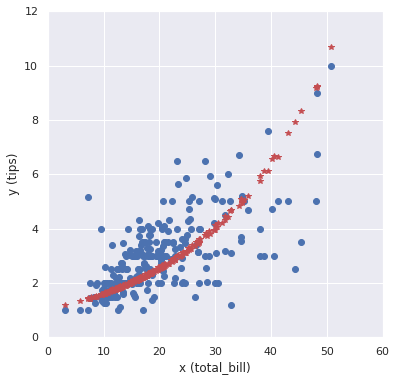
これもなかなか良さそうなモデルですね。サンプル数を増やしても”あてはまりが良い”なら、汎用的なモデルといえそうです。
以上で「統計モデリング実践編」も終了です。
【補足】
少しだけ補足を追記します。
確率分布とリンク関数の組み合わせ
確率分布：正規分布、リンク関数：恒等関数の組み合わせ以外がイメージできない人は以下のスライドが参考になります。
機械学習モデリングと統計モデリング
簡単にですが、機械学習モデリングと統計モデリングを比較したものを書いてみました。
【機械学習モデリング】
交差検証などでモデル出力結果を評価し、ハイパーパラメータチューニングをすることで未知のデータに対しても精度の良い推論ができるモデルを設計する※
※TrainデータとTestデータで確率分布に偏りがあると適切な評価ができない
【統計モデリング】
サンプルの確率分布から真の確率分布を推定し、その推定を考慮したモデル設計により、未知のデータに対しても真の確率分布に”あてはめた”推論ができる※
※統計モデルでは「あてはまりの良さ」を評価することが重要
ちょっと言葉足らずかもしれませんが…
まとめ
統計モデリングの特に一般化線形モデルについて勉強したので、内容をまとめました。
長文なので読むの大変ですが、本記事の内容を理解できれば「統計モデリングの入り口」には立てると感じています。本記事をきっかけに…
という人が増えたら、とても嬉しいです。
また私自身も統計モデリング入門したばかりなので、本記事の内容について間違っている箇所があれば、教えて頂けると嬉しいです。
以下の本で勉強してます。どれも素晴らしい本です。
