こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
今回はベイズ統計モデルの設計手順を整理するために、本記事を書きます。
Contents
統計モデルの設計手順
私の場合は以下の手順で統計モデリングをしています。
- データがどんな数式に従うか考える
- データがどんな確率分布に従うか考える
- 推論結果を考察
- 最初に戻り”より良いモデル”を検討
一言で説明すると『データの背景を考える作業』が統計モデリングだと考えています。
【設計手順❶】データがどんな数式に従うか考える
私が扱う実験データの多くは物理法則に従うので、まず最初に運動方程式を考えます。
ただし 情報不足・知識不足などにより、運動方程式の検討が困難な場合、”あてはまり”が良さそうなモデルを検討します。
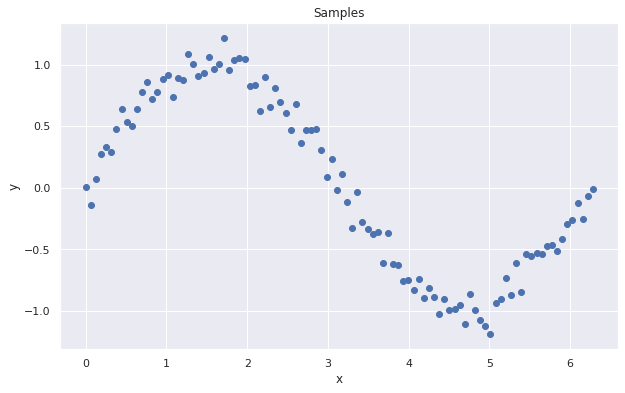
例えば上図のデータなら、以下のモデルだと”あてはまり”が良さそうです。
【モデル】
y = w0 + w1 * x + w2 * x^2 + w3 * x^3
ここでいう”あてはまり”が良いモデルとは、下図の実線(緑)のような”ばらつきの中心”を表現できるモデルという意味です。
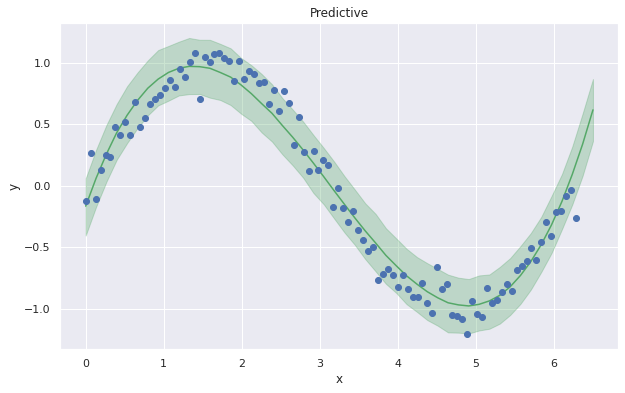
【設計手順❷】データがどんな確率分布に従うか考える
データが”あてはまり”の良いモデルを中心に”ばらつく”と考えたとき、データがどんな確率分布に従うか(どう”ばらつく”か)を考えます。
私が扱う実験データの多くは正規分布に従うので、まず最初に以下の式を採用します。
【確率分布】
μ = y, σ = 1.0
Y ~ Normal(μ, σ)
※σ=1.0が最適か否かは、この時点では不明です
【モデル】
y = w0 + w1 * x + w2 * x^2 + w3 * x^3
機械学習では上記のw0~w3に適当な初期値を与え、最適化アルゴリズムにより一意のw0~w3を算出しますが、統計モデリングではw0~w3も何らかの確率分布に従うという考え方ができます。
各パラメータがどんな確率分布に従うかはケースバイケースですが、悩む場合は初手”正規分布”で良いと思います(あとから変更できるので)。
【パラメータ】
μ = 0, σ = 10
W0 ~ Normal(μ, σ)
W1 ~ Normal(μ, σ)
W2 ~ Normal(μ, σ)
W3 ~ Normal(μ, σ)
※μ = 0, σ = 10が最適か否かは、この時点では不明です
もちろんドメイン知識や仮説から「W0 = 1の固定値を採用」などもOKです。
- 機械学習のように各パラメータや結果を一意に決めるのではなく、不確実性を考慮した設計・推論ができるは「統計モデリング」の強みです
- 全てのパラメータをコンピュータに算出させる必要はなく、ドメイン知識や仮説を組み込んだモデリングが重要です(自論)
【設計手順➌】推論結果を考察
事後分布は?不確実性は?”あてはまり”の良さは?などの推論結果を考察し、σも正規分布に従うと考えるなら、以下のように設計を変更します。
【確率分布】
μ = y
σ ~ Normal(0, 1.0)
Y ~ Normal(μ, σ)
※時間が許す限り何度も設計変更すれば良いと考えています
【設計手順❹】最初に戻り、より良いモデルを検討
最終的に設計したモデルは以下の通りです。
【パラメータ】
μ = 0, σ = 10
W0 ~ Normal(μ, σ)
W1 ~ Normal(μ, σ)
W2 ~ Normal(μ, σ)
W3 ~ Normal(μ, σ)
【モデル】
y = w0 + w1 * x + w2 * x^2 + w3 * x^3
【確率分布】
μ = y
σ ~ Normal(0, 1.0)
Y ~ Normal(μ, σ)
ここで設計した確率分布が事前分布になります。最終的には実験データの分布を考慮し、ベイズの定理やMCMCなどのアルゴリズムを活用して、事後分布を推論します。
この推論を自動化するために、コンピュータとPPLを使います。
あとは仮説検証・検証結果・追加情報・有識者からのアドバイスなど、あらゆる情報を考慮して、上記設計のアップデートを繰り返します。
以上がベイズ統計モデルの設計手順です。
実践!Pyroでベイズ統計モデリング
以降からはPyroによるベイズ統計モデリングを実践します。以下の記事を先に読んでおくと本記事の内容(ソースコード含む)をスッと理解できると思います。
以降からコード書いていきます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns import torch import torch.distributions.constraints as constraints import pyro import pyro.distributions as dist from pyro.infer.mcmc import MCMC,NUTS from pyro.infer import Predictive # 描画スタイル sns.set(style="darkgrid") |
※描画(データを可視化するときの)スタイルは自由に変更してください
サンプルデータ
適当なサンプルを用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
n_samples = 100 epsilon = np.random.normal(0, 0.1, n_samples) X = np.linspace(0, 2 * np.pi, n_samples) Y = np.sin(X) + epsilon # 散布図で可視化 fig = plt.figure(figsize=(10.0, 6.0)) plt.scatter(X, Y) plt.xlabel('x') plt.ylabel('y') plt.title("Samples") plt.show() |

このデータが今回の対象です。
説明変数と目的変数 -torch.tensorに変換–
PyroのバックエンドがPyTorchなので、扱うデータをtorch.tensorに変換します。
|
1 2 3 |
# numpy.ndarrayからtorch.tensorに変換 Xt = torch.tensor(X) # 目的変数:Y = [y0, y1, y2, ... yi] Yt = torch.tensor(Y) # 説明変数:X = [x0, x1, x2, ... xi] |
ベイズ統計モデルの設計
今回はSinにノイズを混ぜたデータ(y = sin(x) + ε)に対し、回帰モデルを設計します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def model(X, Y=None): w0 = pyro.sample('w0', dist.Normal(0.0, 10.0)) w1 = pyro.sample('w1', dist.Normal(0.0, 10.0)) w2 = pyro.sample('w2', dist.Normal(0.0, 10.0)) w3 = pyro.sample('w3', dist.Normal(0.0, 10.0)) # mu = w0 + w1*x + w2*x^2 + w2*x^3 mu = w0 + w1 * X + w2 * X**2 + w3 * X**3 sigma = pyro.sample('sigma', dist.Normal(0.0, 1.0)) pm_Y = pyro.sample('pm_Y', dist.Normal(mu, sigma), obs=Y) return pm_Y |
真のモデルは y = sin(x) ですが、「1周期分のデータからsinを特定するのは困難」という前提で、今回は y = w0 + w1 * x + w2 * x^2 + w3 * x^3 だと”あてはまり”が良いと考えて設計しました。
MCMCの実行
今回はMCMCで事後分布を推論します。
|
1 2 3 4 5 6 7 |
# Run MCMC kernel = NUTS(model) mcmc = MCMC(kernel, warmup_steps=1000, num_samples=2000) mcmc.run(X=Xt, Y=Yt) # print MCMC summary(各パラメータの基本統計量) mcmc.summary() |
変分推論でも良いのですが、下記の参考記事にある各手法の良い点/悪い点を考慮し、十分なサンプル数や演算時間を確保できるなら、初手MCMCで良いと思いました。
事後分布の可視化
以下のコードで各パラメータの基本統計量を出力できます。
|
1 2 3 |
# print MCMC summary(各パラメータの基本統計量) mcmc.summary() |
| mean | std | median | 5.0% | 95.0% | n_eff | r_hat | |
| w0 | -0.26 | 0.04 | -0.26 | -0.33 | -0.19 | 514.54 | 1.00 |
| w1 | 1.98 | 0.06 | 1.98 | 1.88 | 2.07 | 403.04 | 1.00 |
| w2 | 0.90 | 0.02 | -0.90 | -0.94 | -0.86 | 409.40 | 1.00 |
| w3 | 0.09 | 0.00 | 0.09 | 0.09 | 0.10 | 432.71 | 1.00 |
| sigma | 0.11 | 0.01 | 0.11 | 0.10 | 0.13 | 778.02 | 1.00 |
MCMCで算出されたパラメータは以下のコードで取得できます。
|
1 2 3 4 5 6 7 8 9 |
# get param (num_samples=2000) mcmc_samples = mcmc.get_samples() w0 = mcmc_samples["w0"] w1 = mcmc_samples["w1"] w2 = mcmc_samples["w2"] w3 = mcmc_samples["w3"] sigma = mcmc_samples["sigma"] # print("mcmc_samples:", mcmc_samples) |
以下のコードで事後分布を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 可視化 plt.figure(figsize=(15, 10)) plt.subplot(3, 2, 1) sns.distplot(w0) plt.title("Probability Density of w0") plt.subplot(3, 2, 2) sns.distplot(w1) plt.title("Probability Density of w1") plt.subplot(3, 2, 3) sns.distplot(w2) plt.title("Probability Density of w2") plt.subplot(3, 2, 4) sns.distplot(w3) plt.title("Probability Density of w3") plt.subplot(3, 2, 5) sns.distplot(sigma) plt.title("Probability Density of sigma") plt.tight_layout() plt.show() |
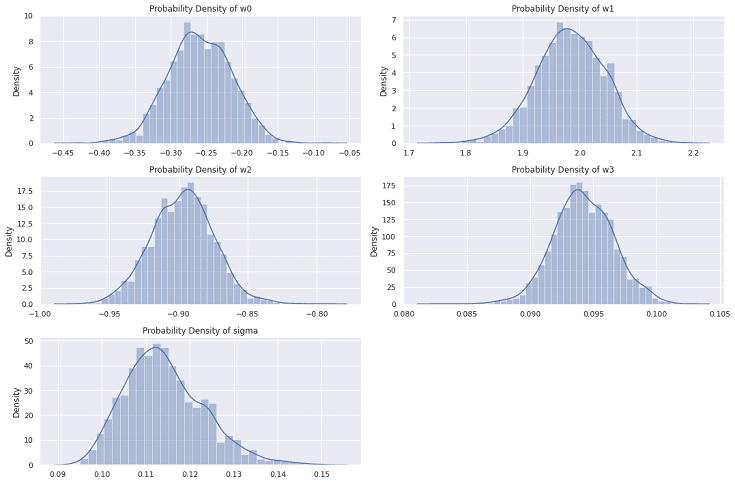
W3 や σ は”ばらつき”が小さいので、再設計するときは固定値にしても良いかもしれません。
推論
以下のコードで X=0~6.5(50サンプル) のときの Y を予測します。
|
1 2 3 4 5 6 7 8 9 |
X_range = np.linspace(0, 6.5, 50) Xt_range = torch.tensor(X_range) # 目的変数:Y = [y0, y1, y2, ... yi] predictive = Predictive(model, mcmc_samples) predict_samples = predictive(X=Xt_range, Y=None) # print(predict_samples) pm_Y = predict_samples['pm_Y'] print(pm_Y) |
以下のコードで予測結果を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 |
mean_Y = pm_Y.mean(axis=0) y_low, y_high = np.percentile(pm_Y, [2.5, 97.5], axis=0) # 可視化 fig = plt.figure(figsize=(10.0, 6.0)) plt.plot(X_range, mean_Y, '-', color='g') plt.fill_between(X_range, y_low, y_high, color='g', alpha=0.3) plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.title("Predictive") plt.show() |

今回は上記の予測に満足したことにしますが…
- x > 6.5 のデータを追加
- 説明変数を追加
- 有識者からのアドバイスを考慮してモデルを見直す
- サンプル数を追加後に確率分布を見直す
など
上記を考慮し、繰り返し統計モデリングにトライすることが多いです。
以上でベイズ統計モデリング実践も終了です。
まとめ
頭の中を整理しながら、ベイズ統計モデルの設計手順をドキュメント化しました。
私の統計モデリングに関する経験値や知見が増えたタイミングで、より良い設計手順を再検討し、本記事の内容も更新できればと思います。
なので…
みたいな知見がある人は情報共有して頂けると嬉しいです。
以下 統計モデリング関連のオススメ書籍