こんにちは!
元制御屋の”はやぶさ”@Cpp_Learningです。
より正確には大学で振動制御やロバスト制御系設計なんかを研究してました。私の経歴についてはプロフィールに記載があるので、気になる人は覗いてみてね。

最近は機械学習によるデータ分析が流行ってますねー
私も勉強してますが、時系列データの分析に機械学習を使っているのを見ると…
と思うときがあります。
機械学習の勉強が目的なら問題ありませんが、もし振動解析のやり方を知らないだけだとしたら…誰かが教えてあげないと!
微力ではありますが、元制御屋の”はやぶさ”が皆様の勉強をサポートさせて頂きます。本記事をきっかけに…
という人や
という人が増えると嬉しいなぁ(*・ω・)ノ♪
Contents
振動の基礎 -振動波形について-
振動解析を説明する前に”振動の基礎”を説明しておきます。
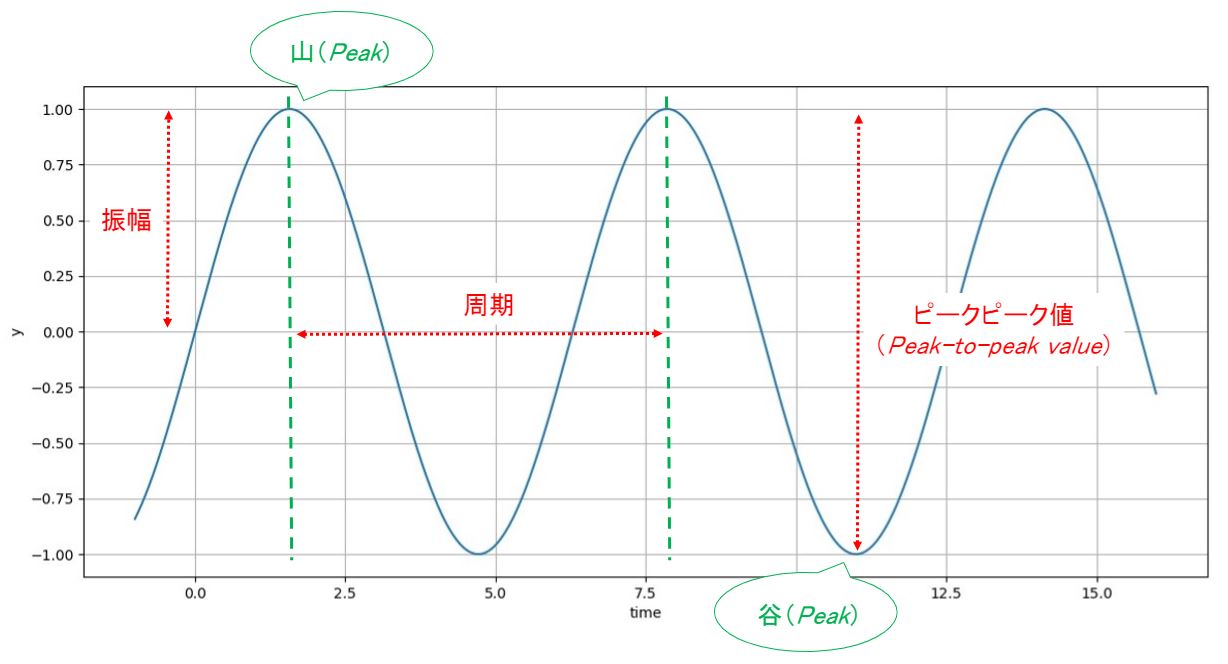
上図の振動波形を例に言葉の定義を確認します。
| 振幅 | 振動の大きさ |
|---|---|
| 周期 | 振動1個分の時間/振動1個分の間隔 |
| 波長 | 振動1個分の距離/振動1個分の間隔 |
| ピーク値 | 振動1個分の最大値または最小値 |
| ピークピーク値 | 振動1個分の最大値から最小値までの大きさ |
| 山 | 振動1個分の最大値 |
| 谷 | 振動1個分の最小値 |
| 周波数 | 単位時間(Hzの場合は1秒)当たりの振動数(周期の数) |
- ”振動”ではなく”波”と説明する場合もあります(例. 波の大きさ)
- 振動波形だと上に凸/下に凸という言葉は使わず、山/谷と言います
- 波の間隔という意味で”周期”=”波長”と説明する場合もあります
- ”周期”と”波長”の単位の違いに注意してください
- 周波数の単位は Hz や rad/sec がよく使われます
振動解析ポイント -周期の観測方法-
参考書や教える人によっては、ピークピーク値の中間…つまり下図の「y=0の位置から振動が始まり、その位置から”周期”を観測する」と説明することがあります。
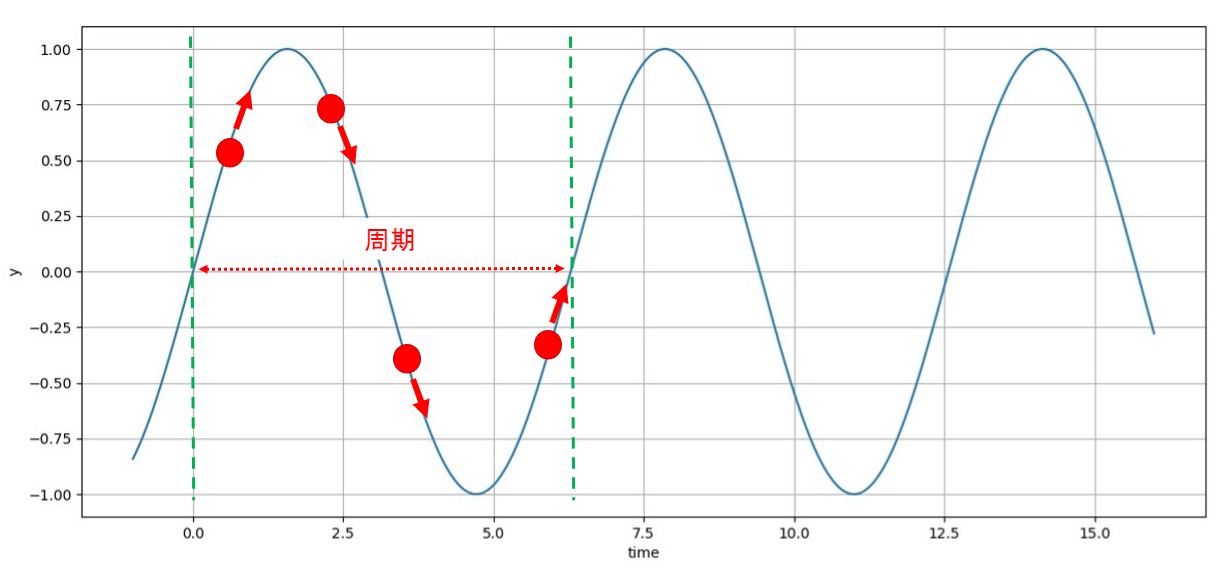
間違いではありません。地震など何かが揺れるときは静止状態から揺れますよね?
ただし、上図のような綺麗な波形なら良いのですが「y=0の位置から振動が始まらないケース」や「ピークピーク値の中間が分かりにくいケース」の波形があります。
(分析対象となる波形は綺麗でないケースの方が多いです。)
そのため、振動波形の山をまず見つけ、その山から次の山までの間隔を”周期”として観測する方が簡単です。
振動波形の性質上、どの位置から観測を開始しても周期(波長)は変わりません。
ピンとこない人は線上を動く赤いボールをイメージしてみて下さい。
赤いボールを一定速度で”1周期(振動1個分)”移動させたとき、どの位置からスタートしてもボールの移動時間(移動距離)は同じですよ(*・ω・)ノ♪
振動波形の周期を確認したい場合は、山から山までの間隔を観測すると良いです。
データ収集
データ分析(振動解析 含む)を勉強したいけど…
という人がいるかもしれません(?) 今の時代だと”ググれ”ば任意のデータセットをダウンロードすることもできますが…
と考え、本記事ではタイトルの通り”ゼロから”…つまり、自力でオリジナルのデータを収集するところから始めます!
【提案】スマホを使ったデータ収集
下記の記事で現役エンジニアである”私の仕事道具”を紹介しており、計器としてスマートフォンの活用をオススメしています。

今回は以下のアプリを使って『腹筋データ(腹筋中の加速度)』を計測します!
※このAppはiOSデバイス向けです。
つまり、本記事では『腹筋データ』を分析対象とします!(振動解析の対象とします!)
みんなが実践できる課題を!
分析するデータについて、色々と言いたい人がいるかも(?)
と思ってますよね…
『腹筋データの分析』に興味がないことは分かってるだ!
ただ…
という想いがあり、以下の理由から『腹筋データ』は振動解析のチュートリアルとしては最適だと考えました。
- 本記事の読者はスマホを持ってる人が多い
- 誰でも一度くらいは腹筋をしたことがある(腹筋の説明を割愛できる)
- 腹筋=周期的な運動
それに…
たかが腹筋ですが、データ分析すると色々なことが分かりますよ!振動解析を楽しく学びたい人は続きも読んでくれると嬉しいです(*・ω・)ノ♪
今回は腹筋データを分析対象にしますが、どんな対象でも『振動解析の基礎』は変わりません。
腹筋データの取得手順
上記で紹介したスマホを使い、腹筋データを取得する方法は以下の通りです。
【腹筋データの取得手順】
- 上記で紹介したアプリ起動
- ”加速度センサー”モードに設定
- サンプリング周期(更新周期)を”0.1”に設定
- ロギング開始
- スマホを握りしめて腹筋開始
- 任意のタイミング(腹筋で疲れたら)ロギング停止
- ロギングした腹筋データ(CSV)をメールで送信
要するに「アプリの使い方」と「スマホの握り方」を説明すれば、私が実践した腹筋データの取得方法を共有できますね。
以下で詳細を説明します。
アプリで加速度を計測する方法(アプリの使い方)
紹介したアプリは直観的な操作が可能です。以降で画面を使いながら説明します。

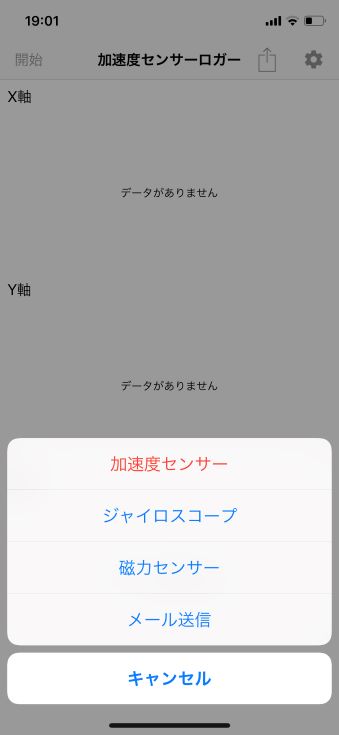
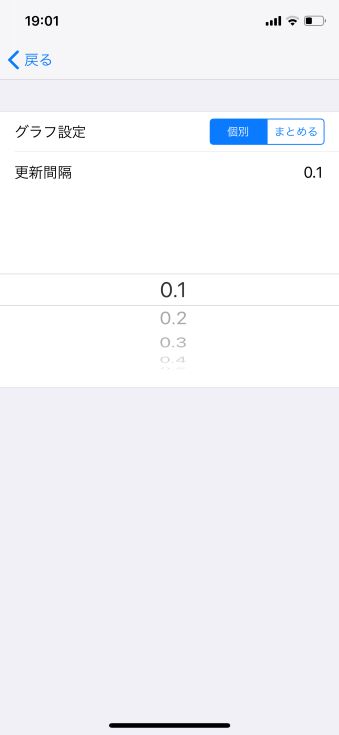
- 上図の左側がスマホを起動した直後の”初期画面”
- 赤□マーク タッチで”加速度センサー”を選択
- 青□マーク タッチでサンプリング周期(更新周期)”0.1”に設定
- 緑□マーク タッチでロギング開始
- (スマホを握りしめて腹筋開始)
- 緑□マーク の文字が”停止”に変わるので任意のタイミングでタッチ
- 赤□マーク タッチで”メール送信”
言葉で説明すると、少し冗長的ですが、実際にアプリを触ってみると簡単にセンシングできることが分かると思います。
スマホの握り方
どんなスポーツ(運動)でも”身体のフォーム”は重要です。腹筋運動も同じで、常に同じフォームで同じペースで運動できるのが理想的です。
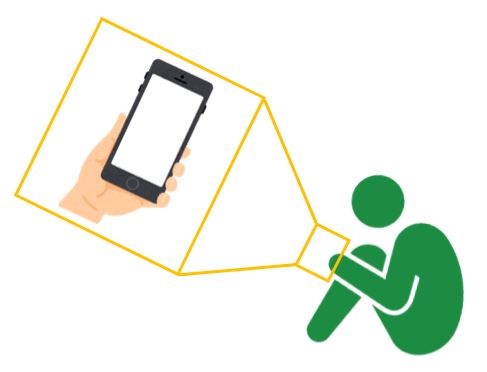
スマホを持ち、かつフォームを崩さずに腹筋をするために、以下のフォームを意識します。
【腹筋のフォーム】
- 肘を垂直に曲げる
- 脇を閉める(胴体と二の腕の隙間を無くす)
- スマホ側面だけが見えるよう(画面が見えないよう)に握る
- 二の腕とスマホが水平になるように手首を動かす
【実践】腹筋データ分析 -振動解析-
以上で説明したフォームで腹筋を疲れるまで行います!また、続けて背筋も疲れるまで行います!
- 腹筋:10~∞回(疲れるまで)
- 背筋:10~∞回(疲れるまで)
そのときの運動データ(加速度)をスマホでセンシングします。
時系列データの中から「分析したいデータ(今回は腹筋データ)」のみを抽出する練習も兼ねて背筋データも取得しました。
データ確認
アプリでは取得したデータ(加速度)はCSV形式でテキストファイルに保存されます。
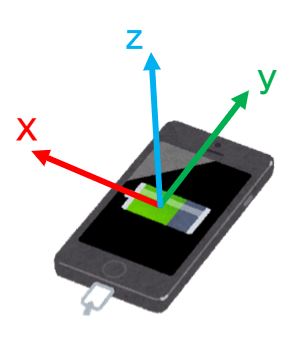
上図のxyz軸に対応した加速度データが存在しますが、今回はx軸のデータのみ分析します。
なので、まずはx軸の加速度データ(x.txt)の中身を確認します。
|
1 2 3 4 5 6 7 8 |
import pandas as pd import matplotlib.pyplot as plt import numpy as np df = pd.read_csv('./test_data/x.txt', sep=',') print(df.shape) df.head() |
↑のコードで以下の表を生成できます。
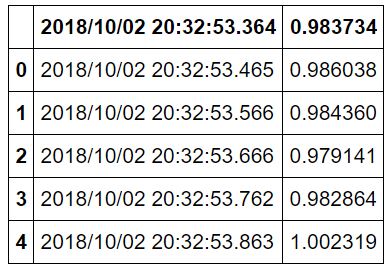
データ加工 -データ可視化の前処理-
次に↑表のデータを可視化(グラフ化)したいのですが…
横軸が日付入りの時間だと扱いにくいので、サンプリング周期(0.1sec)の”time”を生成します。
|
1 2 3 4 5 6 7 8 9 10 |
# df.iloc[行,列] y = df.iloc[:,1] # y.head() tmp_time = np.arange(0, len(y)) tmp_time = tmp_time * 0.1 time_df = pd.DataFrame(tmp_time) time = time_df time.head() |
データ可視化
以下のコードで腹筋データ(x軸方向の加速度)を可視化します。
|
1 2 3 4 5 |
plt.plot(time, y) plt.title("Muscle training !!") plt.xlabel("[s]") plt.ylabel("[m/s^2]") plt.grid(True) |
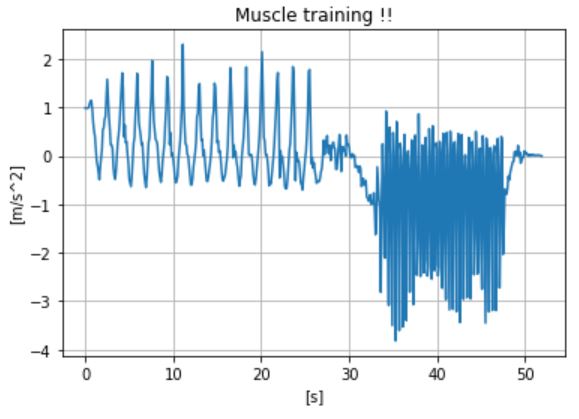
30sec付近で背筋に切り替えたのだろう…スケールが違い過ぎて見にくいので、腹筋データだけを抽出します。
分析データ(腹筋データ)の抽出
「腹筋のデータ分析」という意味では、安定して腹筋が出来ている部分のデータを分析したいので、10~20sec付近のデータを抽出します。
|
1 2 3 4 5 6 7 8 |
# 1列目の100~200行目を抽出 y = df.iloc[100:200, 1] time = time_df[100:200] plt.plot(time, y) plt.title("Muscle training !!") plt.xlabel("[s]") plt.ylabel("[m/s^2]") plt.grid(True) |
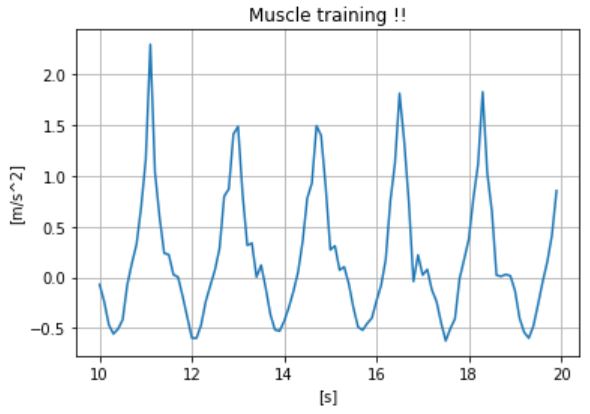
心電図みたい!笑
このような横軸が時間のデータのことを時系列データと呼びますが、制御分野では時刻歴応答と呼ぶことも多いです。また、時間軸が存在するデータを時間領域と呼んだりもします。
以上までがデータ分析(振動解析)を行う前に実施する”前処理”になります。
【実践】振動解析
↑の図を見て、波形が綺麗だし安定したペースで腹筋が出来てそう!…と思うだけでなく、データ分析により「本当に周期的なのか?」を”数値”で確認します。
【解析手法❶】時間領域から周期を観測する
山から山までが1周期なので、その間隔が一定なのかを確認します。
下記のコードでデータフレームに棒グラフを追加することができます。
|
1 2 |
tmp_y_df = df[100:200] tmp_y_df.style.bar() |
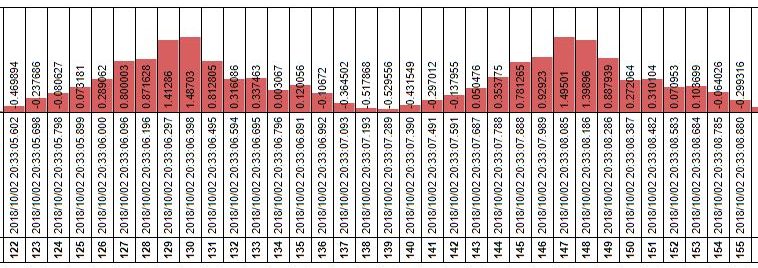
※説明の都合上↑の図は90°回転させています
この棒グラフを使って腹筋データの”周期”を観測します!以下が手順です(*・ω・)ノ♪
【周期性を確認手順】
- 時刻歴応答の13s(130行目付近)の山を↑棒グラフから見つける
- 次の山を見つける
- また次の山を見つける…
- 山から山までの間隔を算出する
実践してみます!まずは山の位置(時間)を確認します。
【山から山までの間隔】
- 一つ目の山:13.0s(130行目)
- 二つ目の山:14.7s(147行目)
- 三つ目の山:16.5s(165行目)
- 四つ目の山:18.3s(183行目)
以下のコードで山から山までの間隔を算出します(まるで電卓)
|
1 2 3 4 5 6 7 |
pitch1 = 14.7 - 13.0 pitch2 = 16.5 - 14.7 pitch3 = 18.3 - 16.5 print('{:.2f}sec'.format(pitch1)) print('{:.2f}sec'.format(pitch2)) print('{:.2f}sec'.format(pitch3)) |
1.70sec
1.80sec
1.80sec
他の山の間隔も確認しましたが、周期:1.6~1.8sで安定したペースで腹筋できていることが分かりました!
データを疑え!考察せよ!!
上記の結果をみて…
と思った人いますか?
確かに安定したペースで腹筋できているのはスゴイけど…腹筋のペースが1.6s/回ってスゴイと思いますか?
言葉や文字に騙されてはダメです!ちゃんと”データ”でスゴイかどうかを分析しましょう!
- 時系列データなどを折れ線グラフだけでなく、棒グラフなど様々なグラフで可視化すると”発見”があります!
- 良い分析とは、誰もが納得できる根拠のある分析です!(自論)
- 根拠のある分析とは、データ(数値)に裏付けされた分析です!(自論)
【解析手法❷】周波数領域から周期を観測する
腹筋のペースが1.6s/回って言われてもペースが速いのか/遅いのか分からないですよね?
例えば、足が速い/遅いなどの”速度”なら…
速度 = 距離 / 時間(m/s)
で求められますよね?つまり、一秒間に何m進んだかを算出することで、速いのか/遅いのかを把握ができます。
同様に、一秒間に何回腹筋(振動)したのかを算出すれば、速いペースか/遅いペースかを把握できます。
「一秒間に何回振動したか」は「周波数 Hz」というので覚えて下さいね。
(周波数の説明は”振動の用語リスト“にも書いてあります)
周波数の算出する手法は色々とありますが…今回は高速フーリエ変換(FFT)を使って周波数を算出してみます!
フーリエ変換とは
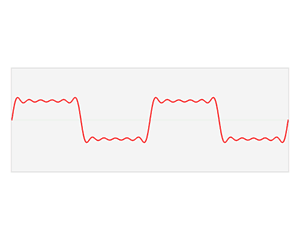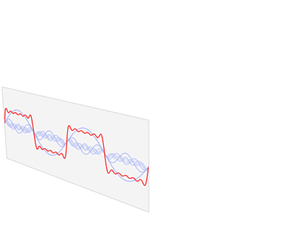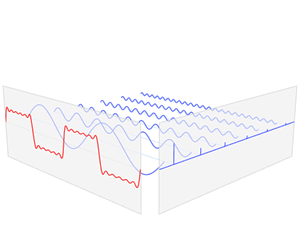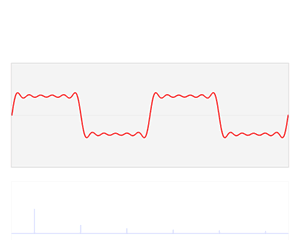
周波数領域の解析では、フーリエ変換などを使い振動波形を周波数成分に分解します。以下がイメージです。
あらゆる振動波形は複数の正弦波を合成することで生成することができます!(超重要!)これは、あらゆる振動波形は複数の正弦波に分解できる!という意味でもあります!
今回の場合、腹筋データの振動波形(時系列データ)をフーリエ変換することで「複数の正弦波(周波数成分)に分解」でき、かつ「各正弦波の大きさ(振幅スペクトル)」を算出できます!
つまり、フーリエ変換などの振動解析により、腹筋データの周波数特性を把握できます!!
- あらゆる振動波形は複数の正弦波を合成することで生成できます!
- あらゆる振動波形は複数の正弦波に分解することができます!
- 振動解析の各手法により振動波形の周波数特性を把握できます!
【実践】フーリエ変換
以下が腹筋データを高速フーリエ変換(FFT)するコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# データ数 N = len(y) # 周波数軸 freq = np.linspace(0, 1.0/dt, N) # 高速フーリエ変換(FFT) F = np.fft.fft(y) # 振幅スペクトル F_amp = np.abs(F) plt.plot(freq, F_amp) plt.xlabel("[Hz]") plt.ylabel("F") plt.grid(True) |
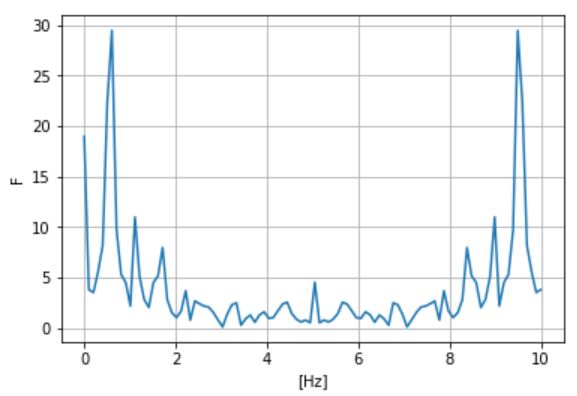
ある周波数(この例では7Hz)で左右対称に”周波数成分”が表示されますが、左側だけ見れば良いので、左半分のピーク付近を拡大します。
本記事では左右対称になる理由を割愛しますが、気になる人は本記事の最後”おまけ”の項目で紹介する参考書などで勉強してみてね!
以下のコードで左側のみ抽出。
|
1 2 3 4 5 6 |
plt.plot(freq, F_amp) plt.plot(freq, F_amp, 'o') plt.xlim([0, 2]) # x軸の範囲(0~2) plt.xlabel("[Hz]") plt.ylabel("[F]") plt.grid(True) |
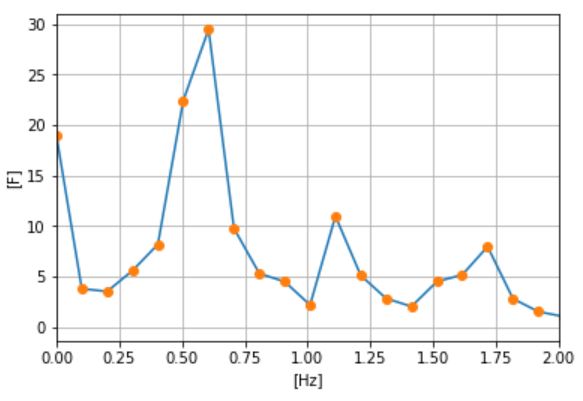
フーリエ変換により、解析した振動の中でも特に大きな周波数成分が0.6Hzであることを確認できました!
つまり…腹筋の周波数が0.6Hzだった!という意味です。
という笑い声が聞こえてきそうですが…ここまでの振動解析でデータ(数値)に裏付けされた根拠のあるデータ分析ができたことに関心を持ってほしいです(*・ω・)ノ♪
『1.6s/回という安定したペースで腹筋ができているが、0.6Hzと遅い!』ということが振動解析により分かりました!
振動解析の豆知識 -複数の周波数成分-
今回はフーリエ変換で大きな周波数成分が一つ(0.6Hz)しか出ませんでしたが…複数の周波数成分が大きく出る場合もあります。
腹筋で例えるなら、辛くてプルプル震えながら腹筋をすると2つの周波数を検出します。
- 高周波:プルプル震えながら
- 低周波:腹筋
今回の振動解析では高周波成分を観測出来なかったので、”安定したペースの腹筋”というだけでなく、以下ような評価もできます!
- まだ余裕がある/疲れていない(?)
- 腕をしっかり固定した綺麗なフォームで運動できている
振動解析などで可視化したデータを考察することで様々なことが分かります!(面白い!)
時間領域と周波数領域のリンク
今回説明した通り”フーリエ変換”を使うことで『時間領域のグラフを周波数領域のグラフ』に変換できました。
また、”逆フーリエ変換”をすると『周波数領域のグラフを時間領域のグラフ』に変換できます。
この他にもフランスの数学者ジョゼフ・フーリエ先生の名を持つ手法は沢山ありますが…
本記事は入門レベルなので、まずはフーリエ○○で『時間領域と周波数領域の行き来ができる!』ということを覚えて頂きたいです!
また、フーリエの名を持つ手法で解析することを『フーリエ解析』と呼ぶことがあります。
フーリエ解析により『時間領域と周波数領域の行き来ができる!』
中学校の数学で時間領域と周波数領域をリンク
ここまでの説明でフーリエ解析により『時間領域と周波数領域の行き来できる!』ということを説明をしましたが…
中学校の数学でも『時間領域と周波数領域の行き来できます!』
【ここまでの復習】
- 腹筋のペース(周期)がT=1.6s/回というのを確認
- 「一秒間の振動数(回/sec)」=「周波数(Hz)」
“T=1.6s/回” の “逆数1/T” を計算すれば、単位は”回/sec”ですよね?
つまり、以下のコードで演算する…
|
1 2 |
fc1 = 1/1.6 print('{:.3f}Hz'.format(fc1)) |
0.625Hz
というフーリエ変換と同じ値を求めることができました。
なので、実は時系列データから”主成分(一番大きな周波数成分)”の周波数を求めることもできました。
しかし、たまたま抽出した振動波形1個分の周波数が0.625Hzだっただけで、別の山から山の振動波形演算すると0.625Hzじゃない可能性もあります!
つまり腹筋運動をしていた30秒間「乱れなく安定したペースで腹筋ができていたか?」を確認するには、やはり周波数領域に変換して各周波数成分を観測するのがベストです!
中学校の数学で簡易的に時系列データから周波数を算出することができます。ただし、任意の時間帯(0~30s)の周波数を観測するなら、フーリエ解析により各周波数成分を確認するのがベストです!
振幅で腹筋の精度と回数を確認する
今までのデータ分析(振動解析)では、主に周波数(周期)に注目することで、腹筋のペースを確認することができました。
ここまでは『安定してるけど遅いペース』という評価でしたが…
回数は分かるけど…
という感じですよね?今回は腹筋の精度を以下のように定義しました。
【精度の良い腹筋の定義】
身体をしっかり起こせている腹筋(顎と膝がつくのが理想的)
精度の良い腹筋をするには、ある程度の勢いがないと難しい…
つまり、山が一定値より大きければ、精度の良い腹筋ができているといえます。
腹筋の時系列データ全体をサッと見たところ、山のピークが1.6m/s^2以上なら精度の良い腹筋といえそうです!
以下のコードで「精度の良い腹筋をした回数」を確認します。
|
1 2 3 4 |
y = df.iloc[0:300, 1] counter = [i for i in y if i >= 1.6] print(len(counter)) # counter |
13
ん?13回しか精度の良い腹筋できてない…だと……?
約30秒間 周期0.6Hz というペースで腹筋してたのだから、30 × 0.6 = 18回できてる予定だった…まぁ仮に18回でも少ないよね!…ってことがデータ分析により分かりますね!
データは嘘つかないので、5回ほど体を起こせてなかったということですね…
以上で腹筋データの分析(振動解析)は終了です!お疲れさまでした!
最後に『振動解析』と『データ分析』のポイントをまとめておきます(*・ω・)ノ♪
【振動解析ポイント】
振動解析では、対象データの”周波数”と”振幅”を明らかにすることが重要です。振動制御まで考えると”位相”も重要です。つまり、対象の周波数特性を把握することが重要です!
【データ分析ポイント】
データ分析では、振動解析などにより算出した数値や可視化したデータ(図)を考察して意味のある情報に昇華することが重要です。(自論)
まとめ -腹筋運動のデータ分析結果-
以上のデータ分析(振動解析)で周波数/振幅/振動数を明らかにできました。
今回の分析対象は腹筋データなので、それに合わせた言葉にすると…
- 腹筋のペースは?
- 体が起きているか?(腹筋の精度は良いか?)
- 腹筋の回数は?
以上のことを腹筋運動のデータ分析から明らかにできました。
振動解析に面白さが伝わったかな?振動解析に興味を持ってくれたかな?
本記事をきっかけに振動解析をもっと勉強したい!という人が現れたら最高に嬉しいです!
時間がある人は以下も読んでみてね(*・ω・)ノ♪
おまけ① -振動解析と異常検知-
本記事の冒頭で…
と書きました。
というのが気になったフクロウ(くるるちゃん@kururu_owl )がいるようなので、簡単に説明しておきます。
私が言っているのは『振動波形の異常検知』という課題に対しての発言です。
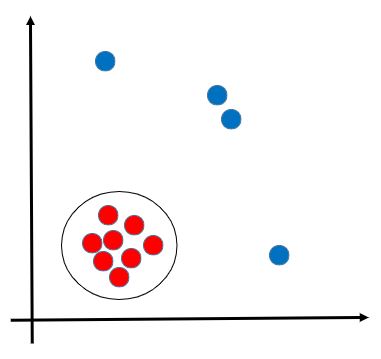
異常検知にも色々ありますが、『上図の赤プロットが正常値だと仮定したとき、赤プロットのグループから外れている異常値(外れ値)の青プロットを検知する!』というのが異常検知の基本的な考え方です。
機械学習の各手法を使うことで正常値と異常値の境界線を算出することができます。
しかし、今まで説明してきた振動解析を使い、対象の周波数特性を把握するだけでも、異常検知は可能です。
本記事では腹筋データの分析を実施しましたが、”ものづくり”の現場ではモータ/ロボット/生産設備などの工業製品を対象にデータ分析⇒異常検知をする場合が多いです。
腹筋運動では実施する人やその日の体調により、取得できるデータが異なりますが…
一般的な工業製品は周期的な運動をするものがほとんどです。
つまり、振動解析により対象(工業製品)の周波数特性を知ることで、その対象が正常に動作しているのか?異常状態なのか?の判断ができます。
外れ値を検知するのが異常検知の基本的な考え方です。そして、”正常と異常の線引き”の算出には、機械学習を含めた様々な手法が存在します。
振動解析による異常検知とは
復習ですが、本記事で振動解析により周波数/振幅/振動数を明らかにし、かつ明らかにした数値を分析し、意味のある情報に昇華させる方法を説明しました。
この周波数/振幅/振動数を分析することで『異常検知』に昇華させることができます。
| 分析する項目 | 異常の種類 |
|---|---|
| 主成分以外の周波数を観測 | ノイズまたは騒音発生 |
| 周波数が安定しない | 動作不安定 |
| 振幅が安定しない | 動作不安定 |
| 振幅が次第に大きくなる | 最悪の場合は対象および周囲を破壊 |
| 振幅が次第に小さくなる | エネルギー不足あるいは外力により力が抑制されている |
『異常とは普段と違うこと!』なので、分析する対象(工業製品)の周波数特性を把握し、普段と違う周波数特性を示していれば『異常』と判断することができます。
また、機械学習を使うにしても時間領域だけでなく、周波数領域に対して機械学習によるデータ分析を行うと、面白い結果が得られるかもしれませんよ(*・ω・)ノ♪
”振動解析”や”機械学習”を便利なツールと考えるなら、目的に合わせてツールを”選択”あるいは”組合わせる”のがカッコイイと思いますよ!
「時系列データの分析」=「機械学習」ではなく、機械学習も含めた数あるツールの中から、目的に合ったツールを”選択”あるいは”合わせ技”ができるとカッコイイと思います!
おまけ② -本の紹介-
おぉ~!フクロウの”くるる”から感嘆の声が聞こえてきた。
その通り!今回は『振動解析で異常検知ができる!』という説明をしましたが、
- 任意の周波数(ノイズや騒音など)を除去する
- 任意の振動を発生させる
などの振動制御にも”フーリエ”や”振動”といった知識が重要です!
喜んで!フーリエ含め”振動”について学べる本を紹介します!
フーリエ解析 -キャンパス・ゼミ シリーズ-
私が学生の頃にお世話になった”キャンパス・ゼミ シリーズ”は工学の参考書というより、数学の勉強用としてオススメの本!もしフーリエ解析に関する講義を受講しているなら、この1冊でテスト対策はバッチリだと思います!
ラプラス変換 -キャンパス・ゼミ シリーズ-
上記と同じ”キャンパス・ゼミ シリーズ”のラプラス変換編!制御分野では、フーリエ変換とラプラス変換の両方を使いますが、研究次第ではラプラス変換ばかり使う人もいます!こちらも勉強用にオススメの本です!
工学基礎 フーリエ解析とその応用
タイトルに工学基礎と付いていますが、基本的には数学の本という印象。フーリエ解析に必要な三角関数/微積分など基礎から説明が始まるので初学者には嬉しい本。”浅すぎず~深すぎず”な内容が丁寧かつコンパクトにまとまっている1冊です。
機械力学Ⅰ -線形実践振動論-
振動に関する研究・開発をするなら、必ず持ってた方が良い1冊!『振動現象を解析』に必要な本質的な内容は全てこの本に凝縮されています。私の知る最強の工学系参考書の1つです。
機械力学Ⅱ -非線形振動論-
上記と同じシリーズの第二弾!内容が非線形振動論なので、そこまでは扱わない…という人も多いかも(?) もし、非線形振動の研究・開発を実施する機会に恵まれたら、この本が参考になると思いますよ!
”振動”の勉強をしたら、修得した知識を分析や制御に応用してみて下さいね!