こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。データ分析力を向上させるために、統計学を勉強しています。
本記事は2標本t検定について勉強した内容の備忘録です。
- 統計学入門したい人
- 統計検定について知りたい人
- 数式を理解してPythonプログラミングで実践したい人
Contents
モチベーション -データ分析と2標本問題-
『AとBを比較して、Aの効果を検証したい』という問題に対し、統計学や機械学習を活用したデータ分析を実施することがあります。例えば、以下のような問題があります。
- 広告の有無で購買量が変化するか?
- 新薬に効果はあるか?
- 地域AとBに生息する同じ種類の魚に地域差は存在するか?
これらは『2つの母集団を比較して、差があるか否かを検証する問題』と考えることができます。
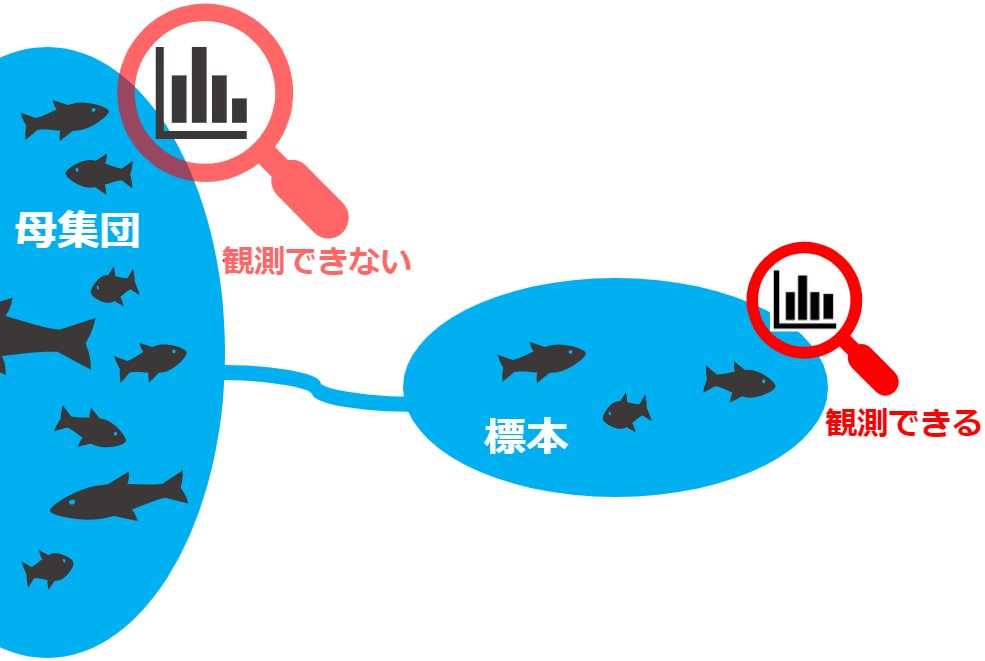
ただし、私たちは母集団から抽出した標本しか観測できないため、『2種の標本から2母集団を推定・比較する2標本問題(two-sample-problem)』として解くことになります。
標本平均の差を比較する
独立した2つの正規母集団 N(μ1, σ1^2)、N(μ2, σ2^2)から大きさm, nの標本を抽出し、標本:x1, x2, …, xm と 標本:y1, y2, …, yn の分布を可視化したものが、下図のパターン1またはパターン2だったとします。
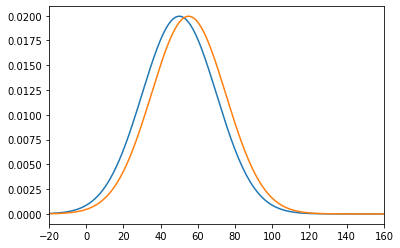
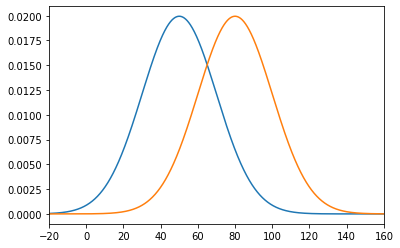
比較すると、パターン1の方が距離が近いので、2つの分布が類似していると判断できます。より正確には、標本平均の差分が小さいので、類似しているといえます。
【標本平均】
mean_X = (x1 + x2 + … + xm) / m
mean_Y = (y1 + y2 + … + yn) / n
【標本平均の差】
mean_X – mean_Y の大小を確認
少し整理すると、『AとBを比較して、Aの効果を検証したい』という問題に対し、以下のフローで検証したことになります。
- 独立した2つの正規母集団から標本を抽出
- 二つの標本A, Bの標本平均を算出
- 標本平均の差の大小を確認
- 差が小さい ⇒ AとBに差がない ⇒ Aに効果はない(Bと変わらない)
仮説検定
上記の簡易的な検証には以下の2つ問題があります。
- 何を基準に標本平均の差の大小を決めれば良いか分からない
- 本当に知りたいのは、標本平均の差ではなく母平均の差 μ1 – μ2
そこで効果の大/小は一旦置いといて、μ1 ≠ μ2 ならAとBに差があるので、Aに効果があるといえそうです。言い換えれば、μ1 = μ2 という仮説を検定し、棄却できれば良しと考えます。
2標本t検定 -母分散は未知だが等しい-
μ1 = μ2 という仮説の検定に、今回は2標本t検定を採用します。なお今回は、2つの正規母集団 N(μ1, σ1^2)、N(μ2, σ2^2) の母分散は未知だが等しい σ1^2 = σ2^2 = σ^2 と仮定します。
2標本t検定のフローは以下の通りです。
- 標本平均の差の分散(pooled variance)を求める
- 標本平均の差を標準化
- 2標本t検定量(two-sample t statisc)を算出
- 2標本t検定
順番に説明します。
標本平均の差の分散を求める
mean_X – mean_Y の分布は正規分布の性質から、N(μ1 – μ2, (σ1^2/m)+(σ2^2/n)) となりますが、今回は σ1^2 = σ2^2 = σ^2 と仮定したので、N(μ1 – μ2, (1/m+1/n)*σ^2) となります。
また母分散 σ^2 が未知と仮定したので、mean_X – mean_Y の分散を以下の式で推定します。
【合併した分散(pooled variance)】
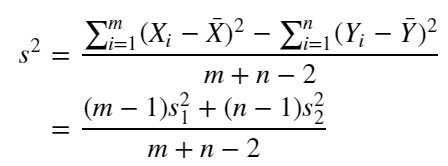
※ S1, S2 は不偏分散
標本平均の差の標準化
続いて、mean_X – mean_Y を標準化します。
【標準化】
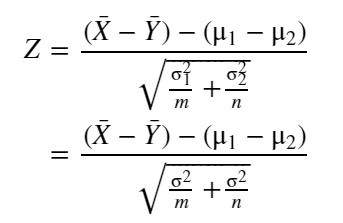
標準化なので、Zの分布は標準正規分布 N(0, 1) になります。
2標本t検定量(two-sample t statisc)
先ほど求めた Z から、以下の2標本t統計量を求めます。なお未知の母分散 σ^2 の代わりに s^2 を使います。
【2標本t統計量】
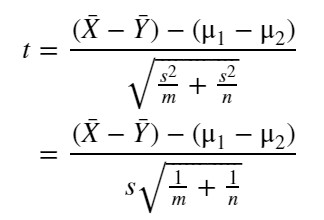
2標本t検定
仮説検定の章で「μ1≠μ2 ならAとBに差があるので、Aに効果があるといえそうです。言い換えれば、μ1=μ2 という仮説を検定し、棄却できれば良し」と説明しました。正確には以下の通りです。
【帰無仮説】
H0:μ1 = μ2
【対立仮説】
両側なら H1:μ1 ≠ μ2
なお単にAとBに差があれば…ではなく「(分布を可視化したとき)BよりAの平均が右側にあれば、またはBよりAの平均が左側にあれば、Aに効果あり」と考えるなら、以下のような対立仮説を採用します。
【対立仮説】
片側なら H1:μ1 > μ2 または μ1 < μ2
さて H0 が正しいなら、μ1 – μ2 = 0 なので、2標本t統計量は以下になります。
【2標本t統計量】
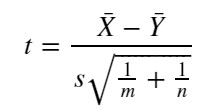
※分母は標準誤差
この t は 自由度:ν=m+n-2の t分布 に従うので、|t| > tα/2(ν) のとき、帰無仮説が棄却されます。
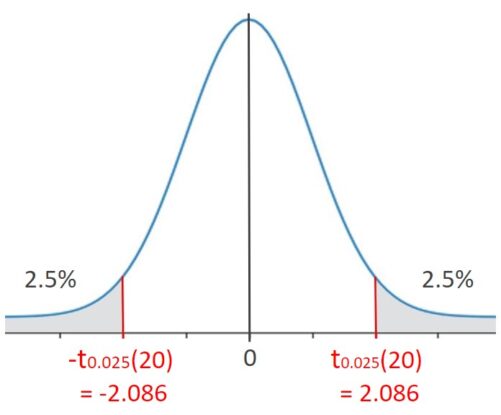
例えば、自由度:ν=20、有意水準:5%(α/2=0.025) のとき、t分布表を参照すると、t0.025(20)=2.086 だと分かります。図で表現すると下図のようになります。
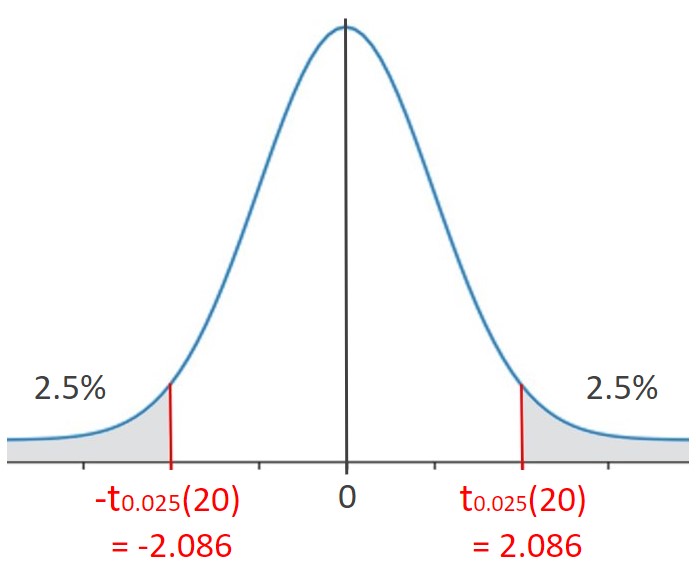
t = ±2.086 となるのは、確率0.05と稀なので、tが上図の灰色の区間に存在するという仮説には無理があります。つまり、帰無仮説 H0:μ1 = μ2 を棄却できます。
あるいはt値からp値を求めて、そのp値が設定した有意水準を下回る場合にも、帰無仮説を棄却できます。
実践!Pythonで2標本t検定
2標本t検定がどんなものか理解できたので、次はPythonで実践してみます。
Import
最初はimportから
|
1 2 3 4 |
import numpy as np import matplotlib.pyplot as plt from scipy import stats from statsmodels.stats.weightstats import ttest_ind |
サンプル生成
独立した2つの正規母集団 N(μ1, σ1^2)、N(μ2, σ2^2)から大きさm, nの標本(サンプル)を抽出します。ただし σ1^2 = σ2^2 = σ^2 と仮定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 母集団の統計量 m = 121 n = 121 mu1 = 50 mu2 = 60 sigma1 = 20 sigma2 = 20 # 標本:X = x1,x2,..,xm、標本:Y = y1,y2,..,yn X = stats.norm.rvs(loc=mu1, scale=sigma1, size=m, random_state=0) Y = stats.norm.rvs(loc=mu2, scale=sigma2, size=n, random_state=1) # X = np.random.normal(loc=mu1, scale=sigma1, size=m) # Y = np.random.normal(loc=mu2, scale=sigma2, size=n) # 分布をヒストグラムで可視化 plt.hist(X, bins=20, alpha=0.3, ec='blue') plt.hist(Y, bins=20, alpha=0.3, ec='blue') plt.show() |
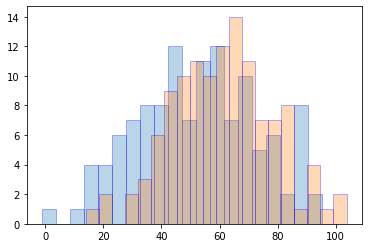
標本を可視化したものが上図です。
標本の統計量を算出
標本の統計量や自由度を算出します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 標本平均 mean_X = X.mean() mean_Y = Y.mean() # 標本分散 var_X = X.var() var_Y = Y.var() # 不偏分散 dvar_X = X.var(ddof=1) dvar_Y = Y.var(ddof=1) # 標本標準偏差 std_X = X.std() std_Y = X.std() # 自由度 dof = m + n - 2 print("mean_X:", mean_X) print("mean_Y:", mean_Y) print("var_X: ", var_X) print("var_Y: ", var_Y) print("dvar_X: ", dvar_X) print("dvar_Y: ", dvar_Y) print("std_X: ", std_X) # np.sqrt(var_X) print("std_Y: ", std_Y) # np.sqrt(var_Y) print("dof: ", dof) |
mean_X: 52.69253472142586
mean_Y: 60.70721318383728
var_X: 433.52810373909466
var_Y: 306.97487395161
dvar_X: 437.14083793692043
dvar_Y: 309.5329979012067
std_X: 20.82133770292136
std_Y: 20.82133770292136
dof: 240
Pythonで2標本t検定量を算出
先ほど求めた統計量から2標本t検定量を算出します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 推定した分散 v = ((m - 1) * dvar_X + (n - 1) * dvar_Y) / (m + n - 2) print("v:", v) # 推定した標準偏差 s = np.sqrt(v) print("s:", s) # 標準誤差 se = np.sqrt(v/m + v/n) print("se:", se) # t値(2標本t統計量)の算出 t_value = (mean_X - mean_Y) / se # t_value = (mean_X - mean_Y) / (s * np.sqrt(1/m + 1/n)) # 上式と同じ print("t_value:", t_value) # p値の算出 p_value = min(stats.t.cdf(t_value, dof), 1-stats.t.cdf(t_value, dof)) * 2 print("p_value:", p_value) |
v: 373.33691791906364
s: 19.321928421331645
se: 2.4841212022408525
t_value: -3.226363695612605
p_value: 0.0014283170541839487
自由度:dof=240、有意水準:5%(α/2=0.025) のとき、t分布表を参照すると、t0.025(20)=1.970 だと分かります。
【帰無仮説】
H0:μ1 = μ2
【対立仮説】
両側なら H1:μ1 ≠ μ2
算出したt値が |t| > tα/2(ν) を満たす(t < -1.970)ので、帰無仮説 H0:μ1 = μ2 は棄却されます。またp値が設定した有意水準を下回っていることも分かります。
実践!SciPyで2標本t検定量
ここまでは、Pythonでゼロから2標本t検定を実践しましたが、SciPyという便利なライブラリを活用して、検定をする方が実用的です。
SciPyで2標本t検定量 -母分散は未知だが等しい-
scipy.stats.ttest_ind()を使えば、たった1行でt値とp値を算出できます。なお母分散は未知だが等しい場合、equal_var=Trueとします(デフォルトでTrueです)。
|
1 2 3 4 5 6 7 8 |
t_value, p_value = stats.ttest_ind(X, Y, equal_var=True) print("t_value:", t_value) print("p_value:", p_value) if p_value < 0.025: print(f"p = {p_value:.3f} のため、帰無仮説が棄却されました。AとBに差があります") else: print(f"{p_value:.3f} のため、帰無仮説が採択されました。AとBに差はありません") |
t_value: -3.2263636956126045
p_value: 0.001428317054183951
p = 0.001 のため、帰無仮説が棄却されました。AとBに差があります
また有意水準を設定したif文で仮説を検定(仮説を棄却できたか否かを確認)できます。
SciPyでウェルチのt検定(Welch’s test) -母分散が等しくない-
母分散が等しくない場合、equal_var=Falseにすることでウェルチのt検定を実施できます。
|
1 2 3 4 5 6 7 8 |
t_value, p_value = stats.ttest_ind(X, Y, equal_var=False) print("t_value:", t_value) print("p_value:", p_value) if p_value < 0.025: print(f"p = {p_value:.3f} のため、帰無仮説が棄却されました。AとBに差があります") else: print(f"{p_value:.3f} のため、帰無仮説が採択されました。AとBに差はありません") |
t_value: -3.226363695612605
p_value: 0.0014336149070709279
p = 0.001 のため、帰無仮説が棄却されました。AとBに差があります
数式の説明は割愛しますが、母分散が等しいときは最初に求めたt値(equal_var=True)と同じになります。
そのため、最初から等分散性を考慮する必要のないウェルチのt検定を実施する方が良いという考え方もあるそうです。詳しくは下記の記事を参考にして下さい。
実践!statsmodelsで2標本t検定量
最後に statsmodels でも検定します。
statsmodelsで2標本t検定量 -母分散は未知だが等しい-
使い心地はSciPyと同様ですが、t値とp値に加え、自由度も算出されます。なお母分散は未知だが等しい場合、usevar=’pooled’とします(デフォルトで’pooled’です)。
|
1 2 3 4 5 6 7 8 9 |
t_value, p_value, dof = ttest_ind(X, Y, alternative='two-sided', usevar='pooled') print("t_value:", t_value) print("p_value:", p_value) print("dof:", dof) if p_value < 0.025: print(f"p = {p_value:.3f} のため、帰無仮説が棄却されました。AとBに差があります") else: print(f"{p_value:.3f} のため、帰無仮説が採択されました。AとBに差はありません") |
t_value: -3.2263636956126027
p_value: 0.001428317054183958
dof: 240.0
p = 0.001 のため、帰無仮説が棄却されました。AとBに差があります
SciPyと異なり、対立仮説に応じて、以下のようにalternativeを設定できます。
【対立仮説:H1】
- ‘two-sided’ (default):μ1 ≠ μ2
- ‘larger’:μ1 > μ2
- ‘smaller’:μ1 < μ2
※上から両側検定、片側検定(右側)、片側検定(左側)
statsmodelsでウェルチのt検定(Welch’s test) -母分散が等しくない-
最後にusevar=’unequal’として、ウェルチのt検定をして終わりたいと思います。
|
1 2 3 4 5 6 7 8 9 |
t_value, p_value, dof = ttest_ind(X, Y, alternative='two-sided', usevar='unequal') print("t_value:", t_value) print("p_value:", p_value) print("dof:", dof) if p_value < 0.025: print(f"p = {p_value:.3f} のため、帰無仮説が棄却されました。AとBに差があります") else: print(f"{p_value:.3f} のため、帰無仮説が採択されました。AとBに差はありません") |
t_value: -3.2263636956126027
p_value: 0.0014336149070709407
dof: 233.18915195086203
p = 0.001 のため、帰無仮説が棄却されました。AとBに差があります
※詳細な説明を割愛しますが、自由度が近似値になります。
まとめ
「ゼロから学ぶ2標本t検定 -Pythonによる実践あり-」というタイトルの通り、以下の点を丁寧に解説してみました。
- なぜ検定をするのか?
- どんな数式を使うのか?
- 実用的なソースコードの書き方は?
色々と調べて、頭の中を整理しながら書いた記事ですが、それもミスがあるかもしれないので、間違っている箇所を見つけた人は教えて頂けると嬉しいです。
本記事が統計学入門者の助けになることを願っています。
統計学を仕事で役立てたい人にオススメの書籍
本記事を書く上で参考にした本や仕事するときに手元にあると便利な本を紹介します。
統計学入門(基礎統計学Ⅰ)
統計学入門のバイブル!噂通りの良書でした。数式が沢山でてきますが、理論に関する丁寧な解説があるので、理解できるまで繰り返し読むことをオススメします。本記事を書く上で最も参考にした本です。
完全独習 統計学入門
統計学アレルギーの人や統計学に挫折した人は、本書で苦手意識を無くすことから始めるのが良いと思います。上記と同じ「統計学入門」というタイトルですが、こちらは更に説明がやさしい超入門書です。
効果検証入門
本記事は「効果を検証するために、検定する」というストーリで解説しています。このストーリ展開は本書を少し意識しています。統計学や機械学習を道具として使いながら、効果検証したい!因果推論したい!という人にオススメの一冊です。
仕事ではじめる機械学習 第2版
近年のAIブームに乗っかり、機械学習を勉強し始めた人も多いのでは?(そう私です)機械学習は面白いし、良書も学習サービスも多いので、どんどん知識を増やせると思います。ただ統計学を疎かにしていると、どこかで躓くと思います。本書の第7章に仮説検定の説明があります。「仕事ではじめる機械学習」という本なのに、なぜ統計学の仮説検定がでてくるのか?機械学習を仕事で使いたい人は、ぜひチェックしてみてください。
以上