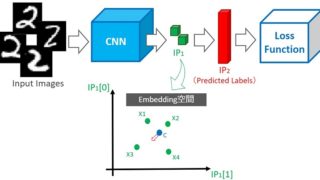
こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。前回、距離学習の記事を書きました。
今回は、深層距離学習（Deep Metric Learning）のSiamese Networkと損失関数のContrastive Lossについて勉強したので、備忘録も兼ねて本記事を書きます。
Contents
深層距離学習（Deep Metric Learning）とは
冒頭で紹介した距離学習（Metric Learning）入門から実践までの記事で深層距離学習の前知識となる「距離とは？」・「空間とは？」・「距離学習とは？」について丁寧に説明しました。
なので、前知識についてはサッパリとした説明のみしておきます。
- 距離の近いか遠いかで同じか否かを判定できる
- 座標ではない特徴量も空間に埋め込むことで距離算出ができる
- 距離学習では、最適な距離を実現するための学習を行う
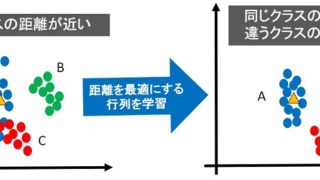
- 最適な距離とは、埋め込み空間内で同じクラスは近く、違うクラスは遠くなる距離のこと
下図が最適な距離のイメージです。
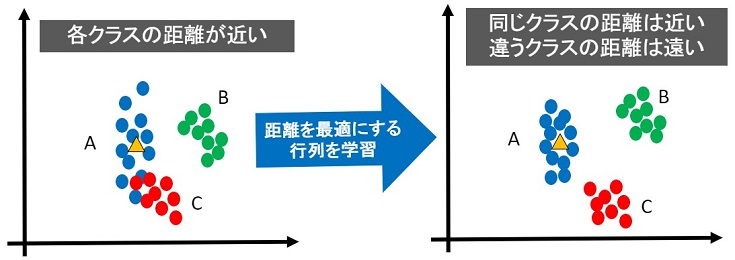距離学習を使えば、最適な距離による同じか否かの判定ができるため、以下のような問題を解決できます。
- データセットのラベル付けが適切かどうか判定（ノイズ判定）
- 画像分類で人と分類したあと、その人が”はやぶさ”か否かを判定
- 物体検出でフクロウ検出し、そのフクロウが”くるる”か否かを判定
など、クラスタリングや異常検知ができる距離学習は問題解決のための強力な武器になります。
この記事で紹介したマハラノビス距離学習では行列Mまたは行列Lの学習により、最適な距離を実現しました。
深層距離学習では行列ではなくニューラルネットワークの学習により、最適な距離を実現します。
Siamese Networkとは
2019年11月時点、様々な手法の深層距離学習が存在します。ただし、数ある手法の中で最初に説明したいのがSimese Network（以下 Simese）です。
Simeseが比較的古い（2006年ごろに提案された）手法だから、最初に説明した方が良いというのもありますが…
最適な距離を実現するアイデアが元制御屋の私にとって、とても納得のいくものだったからです。
まずは、Siameseの概要から説明します。
Siamese Architecture -ネットワーク構造-
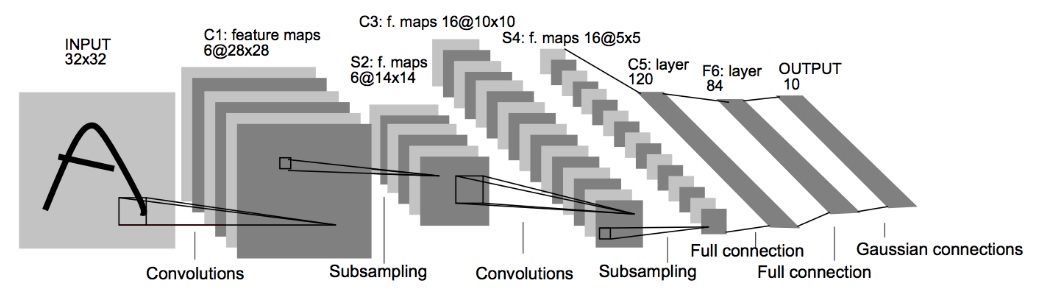
深層学習の勉強をしていると、下図のようなネットワークを目にする機会があると思います。
出展：これはCNNの元祖であるLeNetのネットワーク構造ですが、より高性能なGoogLeNet・ResNet・EfficientNetなど特徴的なネットワーク構造のCNNもあります。
Simeseには特徴的なネットワーク構造はありません…というよりベースネットワークに何を使っても距離学習を実現できます（CNNではなく、単純なNNでも問題ありません）。
Siameseによる推論
Siameseの特徴はネットワーク構造ではなく、ペア画像を入力し、最適な距離を出力する点と後ほど説明する学習アルゴリズムです。
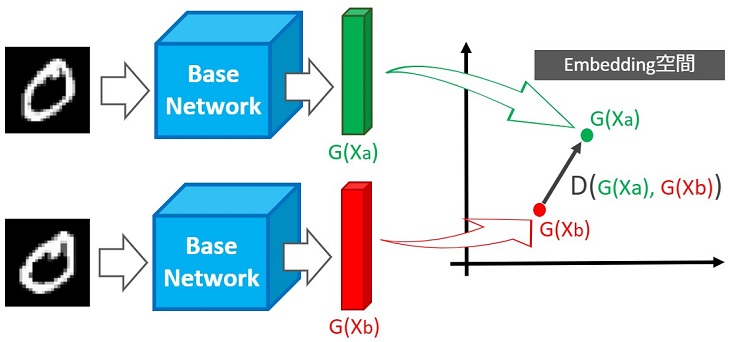簡易的な推論フローは以下の通りです。
【Siameseによる推論フロー】
- ベースネットワーク（CNNまたはNN）にペア画像を入力
- ベースネットワークから出力した特徴ベクトルを空間に埋め込む
- 最適な距離Dを出力する
上図の例では、同じクラス（同じ数字）のペア画像なので、距離Dが小さくなるよう学習します。
一方、違うクラス（違う数字）のペア画像なら、距離が遠くなるよう学習します。
Siameseアルゴリズム概要
学習アルゴリズムの詳細説明をする前に、Siameseが「どうやって最適な距離Dを実現するか？」のイメージを紹介します。
この動画は以下のチュートリアル記事 -Day7- で紹介したゲームの一部です。プレイヤーが操作しているのは猫だけで、ねずみは猫に自動追従しています（可愛い）。
原理（アルゴリズム）としては、猫とねずみを”仮想ばね”で接続することで実現しています。
Siameseも”ばね”の復元力を応用し、最適な距離を実現しています。
例えば、空間に埋め込んだ点Aと点Bが同じクラスなら、A-B間距離を”0”に収束させる”仮想ばね”を接続します。つまり、伸びた”ばね”を縮める方向に力を発生させます。
一方、点Aと点Bが違うクラスなら、A-B間距離が近いときに距離を遠ざける”仮想ばね”を接続します。つまり、縮んだ”ばね”を伸ばす方向に力を発生させます。
Siameseは、ばねの復元力を応用し、最適な距離を実現しています
Siameseアルゴリズム詳細
ここまでの内容がSiameseの概要説明になります。以降からはアルゴリズム詳細を説明します。
具体的には、深層距離学習のSiameseが「どうやって最適な距離Dを実現しているか？」の学習アルゴリズムを説明します。
概要（イメージ）は説明済みなので、数式を交えた詳細説明でも”スッと”理解できると思います。
Contrastive Lossとは
誤解を恐れずに言えば、深層学習は最適化問題を解くアルゴリズムです。最適化問題とは、何らかの数値を最小化あるいは最大化する問題のことで、深層学習の場合は損失関数の出力値：Lを最小化するため、ニューラルネットワークの学習（重みの自動調整）をします。
Siameseでは、損失関数にContrastive Lossが使われます。
【Contrastive Loss関数】
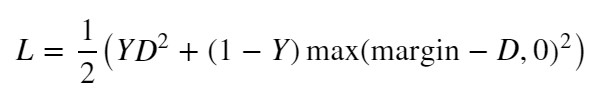L：Loss, Y：ラベル, D：距離, margin：ハイパーパラメータ
Yとmarginについては、あとで詳しく説明しますが、ラベル別で「Y=0 または Y=1」を入力し、「margin=1」がデフォルト設定でよく使われます（要するに学習時に更新するパラメータではありません）。
空間に埋め込んだ2点間距離を算数する距離関数Dには何を使っても良いのですが、本家の論文では、ユークリッド距離を採用しています。
【Euclidean Distance関数】
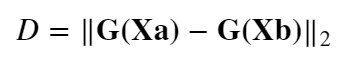
以上から、Contrastive Loss関数の出力値：Lを最適化（最小化）するには、Dを学習（調整）する必要があることを分かってくれると嬉しいです。
そして、距離Dの算出には、ベースネットワーク（CNNまたはNN）の出力値（特徴ベクトル）が使われるため、間接的にベースネットワークを学習（重みを自動調整）することになります。
Mechanical Spring System -距離を近づける”ばね”-
最初に説明した”ばね”のイメージとContrastive Loss関数をリンクさせていきます。
”ばね”の復元力は以下の式で算出できます。
【フックの法則】
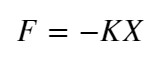F：復元力, K：ばね定数, X：距離
距離に比例して力が発生し、距離Xが”０”に収束すると力Fも”０”に収束します。この法則を応用した距離学習用の損失関数が以下です。
【損失関数❶】
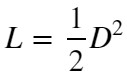L：Loss, D：距離
この式を微分したものが以下です。
【損失関数❶の微分】
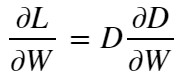
これはフックの法則と同じ形の式です。距離Dに比例して勾配dL/dwが大きくなり、距離Dが”０”に収束するとLossも”０”に収束します。
深層学習では、関数の微分により得られた勾配をもとに重みを調整し、Lossを最適化（最小化）していきます。
深層学習の学習アルゴリズムにより【損失関数❶】を微分し、重みを調整することで”ばね”の復元力に似た仕組みでLossの最適化を実現できます。
この【損失関数❶】を同じクラスの距離を近づけるのに使います（下図(a), (b)参照）
出典：Dimensionality Reduction by Learning an Invariant Mapping
Mechanical Spring System -距離を遠ざける”ばね”-
【損失関数❶】は縮む方向に力が働く”ばね”でした。今から説明する【損失関数❷】は、伸びる方向に力が働く”ばね”です。
【損失関数❷】
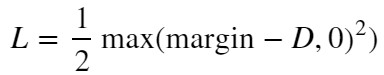L：Loss, D：距離, margin：ハイパーパラメータ
max関数は2値（この例では”margin-D”と”0”）を比較し、大きい方を出力します。そのため、この損失関数では以下の条件分岐で出力値が変化します。
- D < marginのとき ⇒ L = 0.5 * (margin – D)^2
- D >= marginのとき ⇒ L = 0
以上から、距離Dがmarginより遠くないとLossが”０”に収束しません。また、D < marginのとき【損失関数❷】を微分した式が以下です。
【損失関数❷の微分】
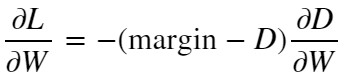
これもX = margin – Dとおけばフックの法則と同じ形の式になります。距離Dに比例して勾配dL/dwが小さくなり、D >= marginでmax関数により強制的にLossを”０”に収束させます。これにより、距離Dが遠い（D >= margin）状態で固定されます。
ここまで説明すると、ハイパーパラメータ：marginの調整方法が分かりますね。距離Dを遠くしたければ、marginを大きく設定すれば良いです。
この【損失関数❷】を違うクラスの距離を遠ざけるのに使います（下図(c), (d)参照）
Mechanical Spring SystemとContrastive Loss
【損失関数❶】と【損失関数❷】を組み合わせたものがContrastive Loss関数です。
【損失関数❶】
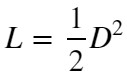
【損失関数❷】
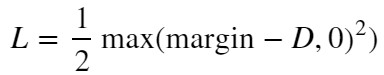
【Contrastive Loss関数】
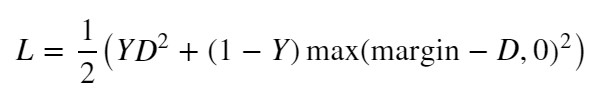L：Loss, Y：ラベル, D：距離, margin：ハイパーパラメータ
さて、【損失関数❶】は同じクラスの距離を近づけるのに使い、【損失関数❷】は違うクラスの距離を遠ざけるのに使うと説明しました。
入力するペア画像に応じて、以下のラベル付けを行います。
同じクラスのペア：Y＝1, 違うクラスのペア：Y=0
改めて、Contrastive Loss関数を見てみて下さい。ラベルＹ（ペア画像）を対比（Contrastive）して、【損失関数❶】と【損失関数❷】を切り替えていることが分かると思います。
この損失関数Contrastive Lossを採用したSimese Networkを学習すると、最終的には、引っ張り合った”ばね”が平衡状態になり、最適な距離に収束します（下図 (e)参照）
実践！深層距離学習 -Siamese Network編-
理論の説明はここまでにして、次は実践しましょう！keras公式ドキュメント-Trains a Siamese MLP-のコードがとても綺麗なので、このコードを解説しながら実践していきます。
また、せっかくなのでTensorFlow2.0に対応させます（基本的にはkeras⇒tf.kerasの変更でOK）
以降で説明するソースコードはGoogle Colaboratoryで動作確認しました。Google Colaboratoryを起動し、最初のセルで以下のコマンドを実行するとTensorFlow 2.x に切替え可能です（2019年11月時点）
%tensorflow_version 2.x
Import
最初はimportから
|
1 2 3 4 5 6 7 8 9 10 11 |
from __future__ import absolute_import from __future__ import print_function import numpy as np import random import tensorflow as tf from tensorflow.keras.datasets import mnist from tensorflow.keras.models import Model from tensorflow.keras.layers import Input, Flatten, Dense, Dropout, Lambda from tensorflow.keras.optimizers import RMSprop from tensorflow.keras import backend as K |
classes and epoch
データセットがMNIST（ラベル：0～9）なのでクラス数=10になります。epochは適当に設定してください。
|
1 2 |
num_classes = 10 # 0～9 epochs = 20 |
ユークリッド距離関数
距離関数Dを作成します。今回はユークリッド距離関数を使います。
|
1 2 3 4 5 6 7 8 |
def euclidean_distance(vects): x, y = vects sum_square = K.sum(K.square(x - y), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon())) def eucl_dist_output_shape(shapes): shape1, shape2 = shapes return (shape1[0], 1) |
Contrastive Loss関数
Contrastive Loss関数（損失関数）も作成します。
|
1 2 3 4 5 |
def contrastive_loss(y_true, y_pred): margin = 1 square_pred = K.square(y_pred) margin_square = K.square(K.maximum(margin - y_pred, 0)) return K.mean(y_true * square_pred + (1 - y_true) * margin_square) |
ペア作成関数（ラベル付け関数）
入力するペア画像に応じて、ラベル付けを行う関数を作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def create_pairs(x, digit_indices): '''Positive and negative pair creation. Alternates between positive and negative pairs. ''' pairs = [] labels = [] n = min([len(digit_indices[d]) for d in range(num_classes)]) - 1 for d in range(num_classes): for i in range(n): z1, z2 = digit_indices[d][i], digit_indices[d][i + 1] pairs += [[x[z1], x[z2]]] inc = random.randrange(1, num_classes) dn = (d + inc) % num_classes z1, z2 = digit_indices[d][i], digit_indices[dn][i] pairs += [[x[z1], x[z2]]] labels += [1, 0] return np.array(pairs), np.array(labels) |
同じクラスのペア：labels＝1, 違うクラスのペア：labels=0
ニューラルネットワーク設計
今回はCNNではなく、簡単なNN（MLP）にします。
|
1 2 3 4 5 6 7 8 9 10 11 |
def create_base_network(input_shape): '''Base network to be shared (eq. to feature extraction). ''' input = Input(shape=input_shape) x = Flatten()(input) x = Dense(128, activation='relu')(x) x = Dropout(0.1)(x) x = Dense(128, activation='relu')(x) x = Dropout(0.1)(x) x = Dense(128, activation='relu')(x) return Model(input, x) |
本家の論文に合わせてCNNにしても良かったのですが、シンプルなNNを採用することで、画像以外にも深層距離学習（Deep Metric Learning）が使えることをアピールできる気がしました（も同じ考えかも？）
Accuracy関数
Accuracy関数まで作成したら、前準備完了です。
|
1 2 3 4 5 6 7 8 9 10 11 |
def compute_accuracy(y_true, y_pred): '''Compute classification accuracy with a fixed threshold on distances. ''' pred = y_pred.ravel() < 0.5 return np.mean(pred == y_true) def accuracy(y_true, y_pred): '''Compute classification accuracy with a fixed threshold on distances. ''' return K.mean(K.equal(y_true, K.cast(y_pred < 0.5, y_true.dtype))) |
MNISTデータセットをダウンロード
MNISTデータセットをダウンロードして、trainデータとtestデータに分けます。
|
1 2 3 4 5 6 7 8 9 |
# The data, split between train and test sets mnist = tf.keras.datasets.mnist (x_train, y_train), (x_test, y_test) = mnist.load_data() x_train = x_train.astype('float32') x_test = x_test.astype('float32') x_train = x_train / 255.0 x_test = x_test / 255.0 # input_shape = (28, 28, 1) input_shape = x_train.shape[1:] # (28, 28) |
データセット可視化
データセットの中身（上から４つ）を確認すると、手書き数字画像が表示されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import matplotlib.pyplot as plt plt.subplot(2,2,1) plt.imshow(x_train[0], cmap='gray') plt.title("label={}".format(y_train[0])) plt.subplot(2,2,2) plt.imshow(x_train[1], cmap='gray') plt.title("label={}".format(y_train[1])) plt.subplot(2,2,3) plt.imshow(x_train[2], cmap='gray') plt.title("label={}".format(y_train[2])) plt.subplot(2,2,4) plt.imshow(x_train[3], cmap='gray') plt.title("label={}".format(y_train[3])) plt.tight_layout() plt.show() |
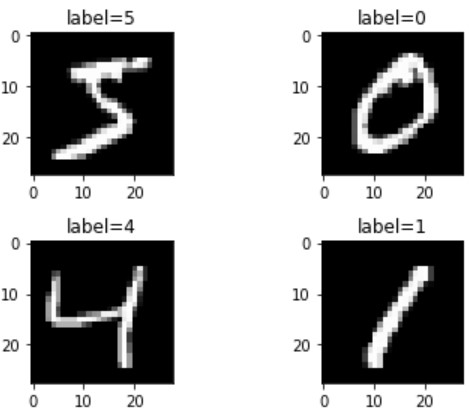
データセットの可視化は必須の処理ではありません。ただし、学習に使用するデータを確認する（じっくり見る）ことで新たな”気づき”があるかもしれません。なので、可視化をオススメしておきます。
ペア画像（ラベル付け）
ペア画像（ラベル付け）を定義します。
|
1 2 3 4 5 6 7 8 |
# create training+test positive and negative pairs digit_indices = [np.where(y_train == i)[0] for i in range(num_classes)] tr_pairs, tr_y = create_pairs(x_train, digit_indices) digit_indices = [np.where(y_test == i)[0] for i in range(num_classes)] te_pairs, te_y = create_pairs(x_test, digit_indices) print(np.shape(tr_pairs)) |
以下のコードで最初の2組を可視化してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
plt.subplot(2,2,1) plt.imshow(tr_pairs[0][0], cmap='gray') plt.title("positive pair {}".format(tr_y[0])) plt.subplot(2,2,2) plt.imshow(tr_pairs[0][1], cmap='gray') plt.title("positive pair {}".format(tr_y[0])) plt.subplot(2,2,3) plt.imshow(tr_pairs[1][0], cmap='gray') plt.title("negative pairs {}".format(tr_y[1])) plt.subplot(2,2,4) plt.imshow(tr_pairs[1][1], cmap='gray') plt.title("negative pairs {}".format(tr_y[1])) plt.tight_layout() plt.show() |
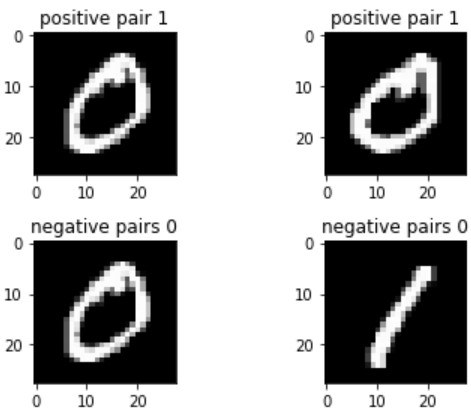
0番目と1番目のペアは以下の通りでした。
- 同じ数字のpositive pair（tr_y[0]=1）
- 違う数字のnegative pair（tr_y[1]=0）
Siamese Network定義
ペア画像を入力し、最適な距離を出力する（2入力1出力系）モデルを生成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# network definition base_network = create_base_network(input_shape) input_a = Input(shape=input_shape) input_b = Input(shape=input_shape) # because we re-use the same instance `base_network`, # the weights of the network # will be shared across the two branches processed_a = base_network(input_a) processed_b = base_network(input_b) distance = Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([processed_a, processed_b]) model = Model([input_a, input_b], distance) model.summary() tf.keras.utils.plot_model(model, to_file = 'model.png', show_shapes = True, show_layer_names = True) |
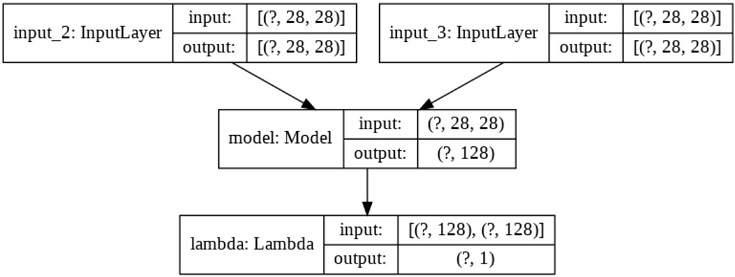
Lambdaを使うことで、自作関数（今回はユークリッド距離関数）をNNの層（Layer）として扱うことができます
学習
fit関数を使って学習します。オプティマイザとしてRMSPropを採用しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# train tr_y = tf.cast(tr_y, dtype='float32') te_y = tf.cast(te_y, dtype='float32') rms = RMSprop() model.compile(loss=contrastive_loss, optimizer=rms, metrics=[accuracy]) H = model.fit([tr_pairs[:, 0], tr_pairs[:, 1]], tr_y, batch_size=128, epochs=epochs, validation_data=([te_pairs[:, 0], te_pairs[:, 1]], te_y,)) plt.title('Train/validation loss') plt.plot(H.history['loss'], label = 'training loss') plt.plot(H.history['val_loss'], label = 'validation loss') plt.grid() plt.legend() plt.show() |
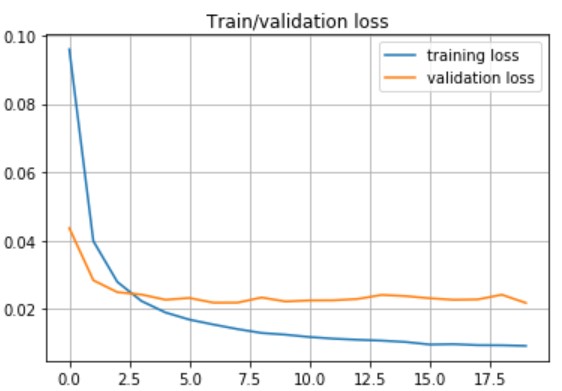
精度確認
自作のcompute_accuracy関数を使って精度を確認します。
|
1 2 3 4 5 6 7 8 |
# compute final accuracy on training and test sets y_pred = model.predict([tr_pairs[:, 0], tr_pairs[:, 1]]) tr_acc = compute_accuracy(tr_y, y_pred) y_pred = model.predict([te_pairs[:, 0], te_pairs[:, 1]]) te_acc = compute_accuracy(te_y, y_pred) print('Accuracy on training set: %0.2f%%' % (100 * tr_acc)) print('Accuracy on test set: %0.2f%%' % (100 * te_acc)) |
- Accuracy on training set: 99.58%
- Accuracy on test set: 97.59%
最適な距離を算出できたのかも簡易的に確認してみます。以下のコードでSimeseの出力結果を可視化します。
|
1 2 3 4 5 6 7 |
plt.figure(figsize = (10,5)) plt.plot(y_pred[0:10], label='distance') # plt.bar(range(0, 10), te_y[0:10]) plt.plot(te_y[0:10],label='Pos or Neg') plt.legend() plt.grid() plt.show() |
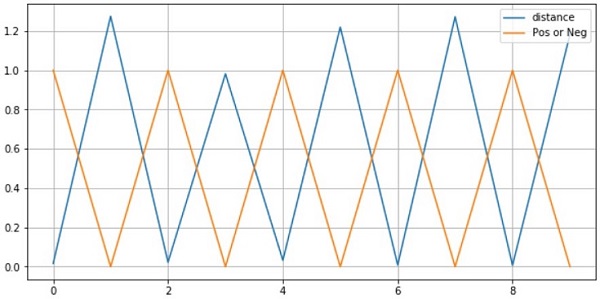
最初の10ペアの結果しか可視化していませんが、結果は以下の通りでした。
- 同じクラスのペア画像（Y=1）の距離は近い（D≒0）
- 違うクラスのペア画像（Y=0）の距離は遠い（D>=margin）
以上で実践も完了です。
まとめ
Siamese NetworkとContrastive Lossの理論から実践まで徹底解説してみました。
Siamese Networkは古い手法だし、既に多くの解説記事があるので、今更という気もしましたが…
機械系・制御系の人たち（もちろん私も含む）が好きそうな”ばね”を応用した学習アルゴリズムについて、丁寧に解説している記事を見つけられなかったので、本記事を書きました。
説明が難しくてまとめるの大変でしたが、本記事を読んでくれた多くの人が…
など、モチベーションが向上するような感想を抱いてくれたら嬉しく思います。
おまけ -本の紹介-
本記事では、深層学習フレームワーク”Keras”を使ってSiamese Networkを設計しました。
”Keras”を自由自在に使いたい人は以下の本が参考になりますよ。
（今回、Lambdaの使い方を思い出すのに、この本が役立ちました）
また、TensorFlow2.0でtf.kerasを使いたい人にも、この本をオススメしておきます。
