こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。距離学習 (metric learning)について勉強したので、備忘録も兼ねて本記事を書きます。
- 第一章：距離（Metric）の基礎
- 第二章：距離（Metric）によるクラスタリング・異常検知
- 第三章：距離学習（Metric Learning）によるクラスタリング・異常検知
本記事の文章構成は上記の通りなので、好きな所から読み進めて下さい。
深層距離学習（Deep Metric Learning）の説明はしません
Contents
【第一章】距離 (Metric)の基礎
最初に距離とは何か？距離からどんなことが分かるか？について説明します。
同じか否かの判定
人生で一度くらいは以下のような会話を聞く機会があると思ます。
- Aさんの顔とBさんの顔はよく似ている
- この店の料理は某有名店と同じ味がする
- あのモノマネ芸人の歌声は人気歌手にそっくりだ
- この地域に生息する動物たちは、日本の動物と同じ特徴がある
❶の顔については、Aさんの顔を基準とし、目・鼻・口などの形や位置が近い場合に似ていると判定できます。
❷の味についても、某有名店の味を数値化したレーダーチャートやグラフを基準とし、それらと同じ数値なら、味も同じといえます。
➌の歌声も同じで、人気歌手の声帯振動や息遣いのタイミングを数値化・基準とし、それに近い数値で唄うことができれば、そっくりな歌声と評価できます。
❹については、ある地域の動物を観察し、行動パターンや身体的特徴の統計量などを把握できたと仮定します。日本で同様の観察を行った結果、似た分布の統計量を観測できたなら「ある地域と日本の動物は特徴が同じ」と判定できます。
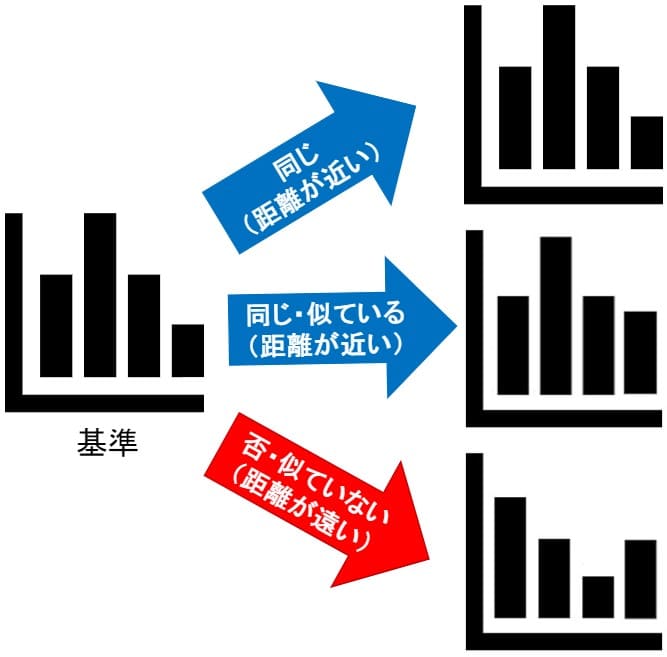４つの異なる例を挙げましたが、どの例でも「何らかの数値データを基準とし、その基準から遠いか近いかで、同じか否かを判定できる」という部分が共通点といえます。
と思った人がいるかもしれませんが、視覚情報＝画像（この例では顔写真）だと考えれば、画像は画素の集合体で行列（数値データ）として扱えます。
距離や空間について
「基準から遠いか近いかで、同じか否かを判定できる」と説明しました。つまり、基準Aと対象Bの距離を算出できれば、同じか否かを判定できます。
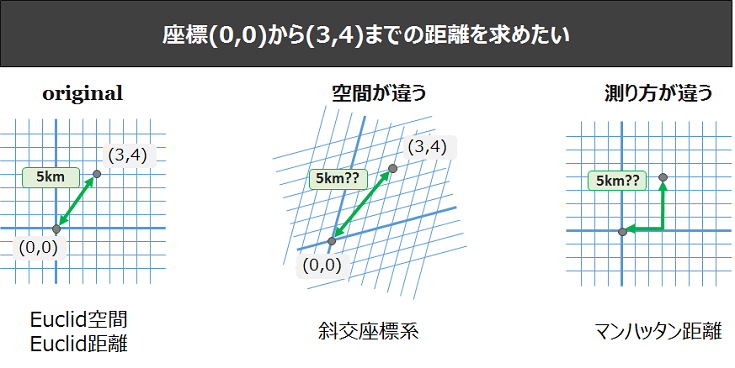
距離といえば、三角形の斜辺を求めるときに使う「三平方の定理」があります。この定理で算出できる距離は、正確にはユークリッド距離と呼ばれています。
ユークリッド距離以外にもマンハッタン距離やチェビシェフ距離などがあります。各距離を比較した面白い記事があるので紹介します。
地球上のA地点に住む織姫とB地点に住む彦星のAB間距離を様々な手法で算出した結果、ユークリッド距離では”16.91km”・マンハッタン距離では”20.9km”となり、演算方法の違いで距離が変わることが分かります。
もし、この記事の登場人物としてC地点に住むデネブ君を追加した場合、演算方法の違いでAB間距離とAC間距離の関係は以下のようになるかもしれません。
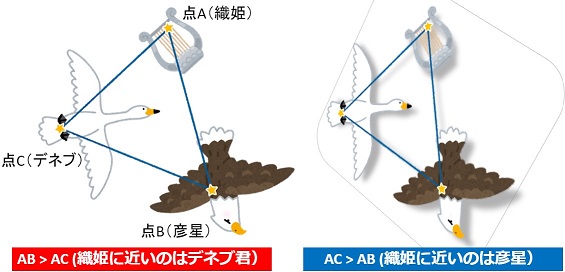
デネブ君は織姫に近づくような移動をしていないのに、採用する”距離”によっては彦星よりも織姫との距離が近くなるので、彦星が嫉妬するかもしれません。
つまり、目的に応じて「どんな距離関数が最適か？」を考える必要があります。ちなみにこの記事では「遠距離恋愛する二人（織姫と彦星）の距離が最も小さくなる距離関数を見つける」という問題設定をしていると感じました。
- ユークリッド距離以外にも様々な距離がある
- 物理的な移動がなくても距離関数（演算）の違いで2点間距離が変わる
特徴量と埋め込み空間（Embedding Space）について
織姫と彦星の例は、日常会話でよく使う距離（道のり）の話題だったので、分かりやすかったと思います。同様に、冒頭で説明した４つの例「AとBの数値データ（特徴量）が同じか否かの判定」も距離の話題です。
❷この店の料理は某有名店と同じ味がする
❷の例で説明してみます。味覚には、甘味・酸味・塩味・苦味・うま味の5つの特徴量があると言われています。例えば、A~C店に関する以下のテーブルがあったとします。
| 店の名前 | 甘未 | 酸味 | 塩見 | 苦味 | うま味 |
| A | ５ | ２ | ２ | ３ | ５ |
| B | ４ | １ | １ | １ | ５ |
| C | ４ | ２ | １ | ３ | 1 |
※単純な５段階で表記しています
全ての特徴量を使っても良いのですが、簡単に説明するため、２つの特徴量を選定して使います。
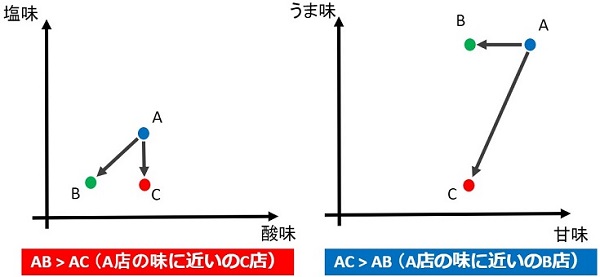
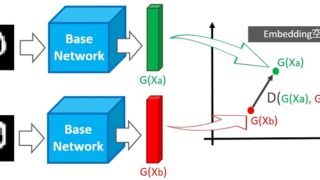
上図のように特徴量を空間（この例では二次元空間）に埋め込むことで、距離を算出できるようになります。つまり、地図上の座標でなくてもデータ（特徴量）を空間に埋め込むことで距離を求めることができます。
また、各ユークリッド距離（三角形の斜辺が最も距離が遠い）を算出すると、埋め込み空間（Embedding Space）の違いで、距離が変わってくることが分かります。
素人なので”味”の正解は判定できませんが、私が料理するときは「うま味」と「甘味」を意識して調理しています。なので「A店と味が近い店はB店・C店どっち？」という問題設定なら『AとBが近く、AとCが遠くなるように埋め込み空間を生成』すると思います。
- データ（特徴量）を空間に埋め込むことで距離を算出できる
- 生成する埋め込み空間により、距離は変化する
【第一章】まとめ -距離（Metric）の基礎-
ここまでの内容を整理します。
「何らかの数値データを基準とし、その基準から遠いか近いかで、同じか否かを判定できる」というのが基本かつ重要な概念です。
「基準から遠いか近いか」というのは距離から判定することできます。ただし、様々な距離の表現方法があるので、目的や問題設定に応じて最適な”距離（Metric）”を採用する必要があります。
また、座標情報ではない特徴量でも、空間に埋め込むことで距離を算出できるため、あらゆる特徴量に対し「距離による同じか否かの判定」が可能です。ただし、”距離”と同じように、目的や問題設定に応じて最適な”埋め込み空間（Embedding Space）”を生成する必要があります。
- ユークリッド距離以外にも様々な距離がある
- 座標情報ではない特徴量でも、空間に埋め込むことで距離算出が可能
- 目的・問題設定次第で最適な距離関数や埋め込み空間が変わる
- 問題設定としては「AB間距離は近く、AC間距離は遠くなる空間・距離を見つける」というものが多い
ここまでが『距離（Metric）の基礎』に関する内容でした。基礎だから単純というわけではなく、奥が深いことが伝わると嬉しいです。
また、データ分析を主軸にした説明を心掛けたので、第一章の内容だけでも「正誤判定」や「クラスタリング・異常検知の前処理」などで役立つと考えています。
第一章（完）
…ここまで読んで、まだ元気な人は第二章 -距離（Metric）によるクラスタリング・異常検知-も読んでみて下さい。
【第二章】距離 (Metric)によるクラスタリング・異常検知
第一章で説明した通り、最適な距離関数と埋め込み空間を採用することが重要です。
第二章では、第一章の内容を踏まえ「距離（Metric）によるクラスタリング・異常検知」について説明します。
分布と距離
第一章では「点A（基準）に近いのは点B・点Cどっち？」という問題設定でいくつか例を説明しました（下図の例など）。
ただし、問題によっては「任意の距離（閾値）よりも遠いか近いかで同じか否かを判定」したいときがあります。
❹この地域に生息する動物たちには、日本の動物と同じ特徴がある
❹の例で説明してみます。まずは、埋め込み空間を生成します。
- 点A：この地域（地域A）に生息する動物たち
- 点B：日本以外に生息する動物
- 点C：日本に生息する動物
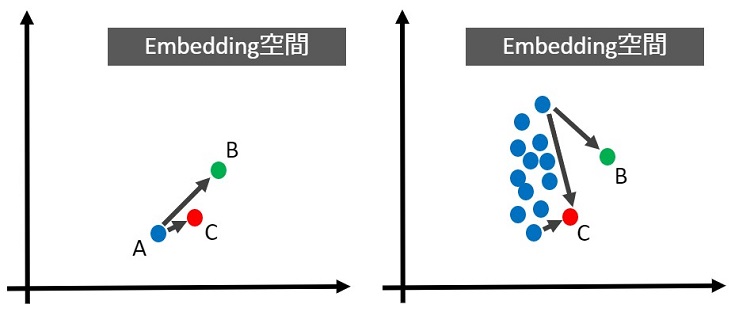
上図（左）の場合、第一章のように点Aとの距離を比較すれば、点Cが近いのは明らかです。しかし、地域Aに生息する”動物たち”と複数形なので、実際には上図（右）になると考えられます。
すると、上図（左）では明らかにAB＞ACだったのに対し、上図（右）ではAC＞ABにも見えます。これは、基準点および基準距離が曖昧なために、生じた問題です。
最適な距離（閾値）の決め方
基準点の決め方はケースバイケースですが、分布の重心・平均値・中央値などを採用するケースが多く、今回は下図の 点▲を基準点 とします。
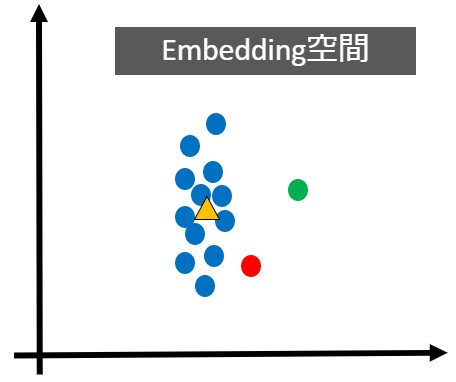この 点▲の基準点 から距離が近いと地域Aに生息する動物（あるいは特徴が同じ動物）、距離が遠いと地域A以外に生息する動物（あるいは特徴が異なる動物）という距離による分類ができます。
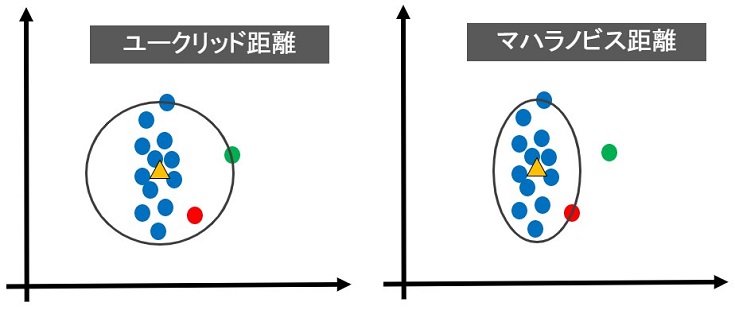基準点から最も離れた青い点のユークリッド距離を算出し、その距離を半径とする円を描き、円の内側（半径よりも近い）なら、地域Aに生息する動物と同じクラスという分類ができます。
しかし、上図（左）を見て分かる通り、ユークリッド距離を使った場合、赤・緑含め全てが同じクラスという分類になります。
一方、マハラノビス距離は相関関係（分散）を考慮して算出されるため、分布の形にフィットした距離を算出できます。その結果、上図（右）のようになり、緑は地域Aに生息する動物とは違うクラスという分類になります。
このように、機械学習を使わず距離によるクラスタリングや異常検知ができることが分かります。
最適な埋め込み空間の生成と最適な距離関数を採用することで、機械学習を使わず、距離によるクラスタリングや異常検知ができます
実践！マハラノビス距離による異常検知
本記事ではマハラノビス距離の概要しか説明しませんでしたが、以下の記事を読めば、マハラノビス距離の詳細を知ることができます。
また、この記事の（実践編）もあり、マハラノビス距離による異常検知を実践しています。勉強のために、マハラノビス距離関数を自作するも良し、scikit-learnのマハラノビス距離関数を使うも良しです。
第二章（完）
…もう疲れたかな？まだ元気な人は第三章 -距離学習（Metric Learning）によるクラスタリング・異常検知-も読んでみて下さい。
【第三章】距離学習 (Metric Learning)によるクラスタリング・異常検知
第二章で、機械学習を使わず距離によるクラスタリングや異常検知を実践できると説明しました。
しかし、問題によっては距離のみで解決できない場合もあります。
第三章（最終章）では、あらゆる問題解決に役立つ強力な武器「距離学習（Metric Learning）」について説明します。
距離の近いクラスの分類
第二章では「青い点群と同じか否か」という問題に対し、マハラノビス距離による判定ができることを説明しました（下図参照）。
しかし、「同じ特徴をもつ動物」ではなく「生息地域別」で分類したい場合、下図のような3クラスに分類する必要があります。
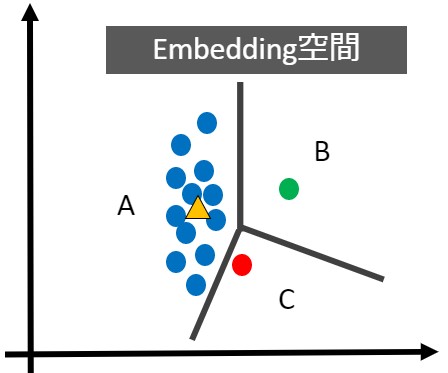
この場合、距離による分類は困難かもしれませんが、機械学習を使えば分類できそうです。ただし、下図のような場合はどうでしょう？
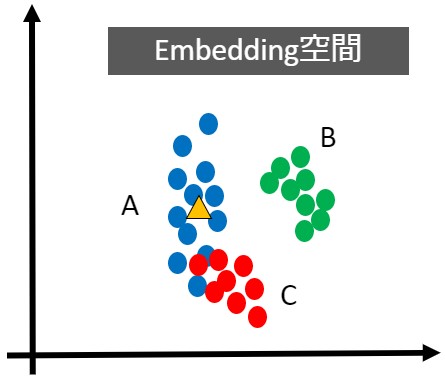
AクラスとCクラスの距離が近すぎて、分類困難ですね。
最適な空間を生成できてない可能性もありますが、ラベル（生息地域）が違うだけで同じ特徴をもつ対象（動物）に対し、綺麗に分布が分離している埋め込み空間を生成するのは難しいです。
このような問題を距離学習（Metric Learning）で解決します。
距離学習（Metric Learning）とは
距離が近すぎて分類が困難なら「同じクラスは距離が近く、違うクラスは距離が遠くなるように移動」させれば良いのです。
距離学習に限らず、ある空間の任意の点を移動させる場合、行列演算を使います。
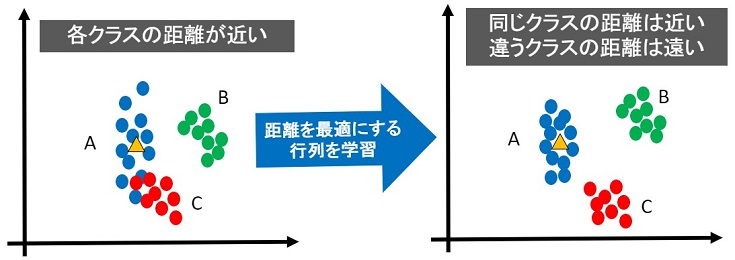距離学習では、上図のように最適な距離にする行列（の各要素）を学習します。
というのが気になる人は、以下の記事が参考になります。行列Mまたは行列Lを学習することで、各クラスの距離を最適化できることが分かります。
実践！距離学習（Metric Learning）
scikit-learn-contrib/metric-learnを使えば、様々な距離学習を簡単に実践できます。
今回は、第二章で説明したマハラノビス距離の学習を実践します。
scikit-learn-contrib/metric-learnをインストール
最初に、以下のコマンドで距離学習用のパッケージをインストールします。
pip install metric-learn
前準備はこれだけです。以降からはソースコードを作成していきます。
Import
必要なライブラリをimportします。
|
1 2 3 4 5 6 7 8 9 |
from sklearn.manifold import TSNE import metric_learn import numpy as np from sklearn.datasets import make_classification, make_regression # visualisation imports import matplotlib.pyplot as plt np.random.seed(42) |
Loading our dataset and setting up plotting
距離学習したくなるようなダミーデータを検討します。
【ダミーデータ】
- 100 points in 3 classes with 2 clusters per class
- 5 features, among which 3 are informative (correlated with the class labels) and two are random noise with large magnitude
以下のコードでダミーデータを生成します（本当は何らかの実データを使いたかった…）
|
1 2 3 4 |
X, y = make_classification(n_samples=100, n_classes=3, n_clusters_per_class=2, n_informative=3, class_sep=4., n_features=5, n_redundant=0, shuffle=True, scale=[1, 1, 20, 20, 20]) |
Visualization
第一章の例「A店と味が近い店はB店・C店どっち？」で5つある特徴量から2つを選定して埋め込み空間の生成および可視化を行いました。実は、全ての特徴量を使わなかったのは、以下ような理由があったからです。
- 特徴量選定の重要性を伝えたい
- 5次元データの埋め込み空間を図で表現できない
今回は、t-SNEで5次元データを次元削減し、2次元データにすることで可視化を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def plot_tsne(X, y, colormap=plt.cm.Paired): plt.figure(figsize=(8, 6)) # clean the figure plt.clf() tsne = TSNE() X_embedded = tsne.fit_transform(X) plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, cmap=colormap) plt.xticks(()) plt.yticks(()) plt.show() |
本記事では説明の都合上、2次元データの例を多用しましたが、多次元データでも距離学習を適用できるし、次元削減することで2Dの可視化が可能なことを理解して頂けると嬉しいです。
Plot the dataset
先ほど定義した関数で3クラス（100プロット）のデータを2Dで可視化します。
|
1 2 3 |
plot_tsne(X, y) |
クラスタリング困難な距離の近いデータセットであることが分かります。
このような各クラスの距離が近すぎるデータはクラスタリング困難なので、同じクラスのデータは距離が近く、違うクラスのデータは距離が遠くなるように距離学習を行います。
Mahalanobis Metric for Clustering
様々な距離学習がありますが、今回はマハラノビス距離学習を実践します。
【アルゴリズム概要】
MMC(Mahalanobis Metric for Clustering) is an algorithm that will try to minimize the distance between similar points, while ensuring that the sum of distances between dissimilar points is higher than a threshold. This is done by optimizing a cost function subject to an inequality constraint.
以下のコードで学習します（すごく簡単！さすがscikit-learnですね）
|
1 2 3 4 |
mmc = metric_learn.MMC_Supervised() X_mmc = mmc.fit_transform(X, y) plot_tsne(X_mmc, y) |
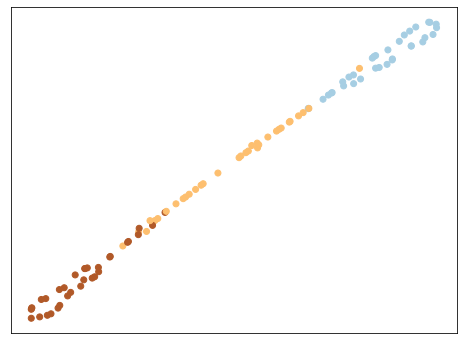
マハラノビス距離学習により、同じクラスの距離が近くなってますね。あとは機械学習などを使えば、分類できそうですね。
KISSME（Keep It Simple and Straightforward MEtric）の理論から実践まで
scikit-learn-contrib/metric-learnには、様々な距離学習関数がありますので、本記事で説明していない距離学習も是非実践してみてください。
また、scikit-learnにはないKISSME（Keep It Simple and Straightforward MEtric）は以下の記事で理論から実践まで説明していますので、こちらも是非実践してみて下さい。
まとめ
当初、深層距離学習（Deep Metric Learnig）に関する記事を書く予定でした。
しかし、深層距離学習を理解するための前知識として、距離学習（Metric Learnig）を先に説明した方が良いと考えました。
また、距離学習を理解するには「距離とは？空間とは？」といった基礎の説明も必要だと思い、以下の文章構成で本記事を書きました。
- 第一章：距離（Metric）の基礎
- 第二章：距離（Metric）によるクラスタリング・異常検知
- 第三章：距離学習（Metric Learning）によるクラスタリング・異常検知
第三章もある長文ですが、距離学習の入門から実践までカバーできてと思います（結構書くの大変でした！）
深層距離学習についても、いつか書きたいと思います（いつか…）
本記事をきっかけに、距離学習（Metric Learning）を実践しました！という人が現れたら最高に嬉しいです。
第三章（完）
おまけ -問題解決に使える武器たち-
(突然でてきたフクロウの”くるる”@kururu_owl が今日も可愛い)
本記事の冒頭で４つの例を提示しているに…
➌あのモノマネ芸人の歌声は人気歌手にそっくりだ
➌の例だけ、一切触れてないよね？
でも以下ことは説明済みだよ。
➌の歌声も同じで、人気歌手の声帯振動や息遣いのタイミングを数値化・基準とし、それに近い数値で唄うことができれば、そっくりな歌声と評価できます。
くるるちゃん振動や信号処理については以下の記事で勉強済みでしょ？
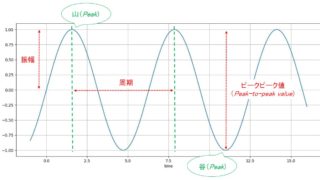
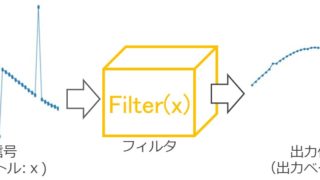
深層学習（LSTM）による時系列データ予測もやったことあるよね？
それで、今回は距離学習入門もしたと…
くるるちゃんは既に問題解決に使える「信号処理」・「振動解析」・「機械学習」・「距離学習」など、たくさんの武器を持ってる状態だよ。今のくるるちゃんなら、自力で➌の例を実践できると思うよ。
あらあら。好奇心旺盛に成長して先生は嬉しいです！笑
本サイト：はやぶさの技術ノートで公開している記事を自分なり理解・吸収できれば、問題解決の武器になります。
問題に対し、あらゆる解決手段を提案・実践できるエンジニアってカッコイイと思いますよ！くるるちゃんのように➌の例を色々なアプローチで実践してみませんか？
改めて…
おまけ（完）
