こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。仕事でもプライベートでも機械学習で色々やってます。
今回はGraph Neural Network(以下 GNN)について勉強したので、備忘録も兼ねて本記事を書きます。
Contents
データ構造とグラフ
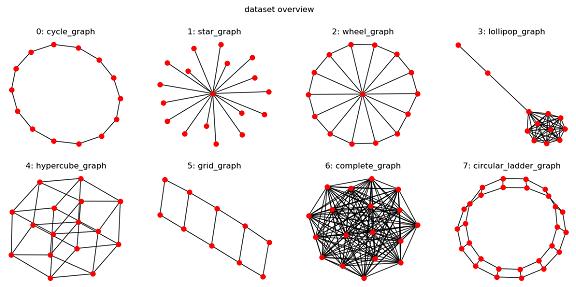
ここでいうグラフとは折れ線グラフや棒グラフではなく、下図のようなデータ構造のことをグラフと呼びます。
例えば、以下に示すネットワークや分子構造、3Dデータなどもグラフといえます。
- インターネット
- Web
- 交通網
- SNS(FacebookやTwitterなど)
- 分子構造(化合物など)
- 神経回路
- 3Dデータのポリゴン
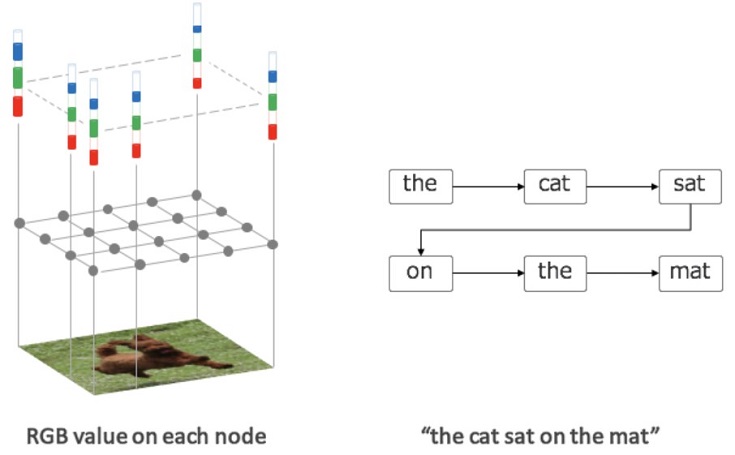
データとデータが繋がったものという意味で、画像(隣り合うピクセル)やテキスト(文字列)もグラフとして表現できます。
グラフとは -ノードとエッジなどの用語について-
SNSや分子構造などの様々なデータが下図のようなグラフで表現できます。
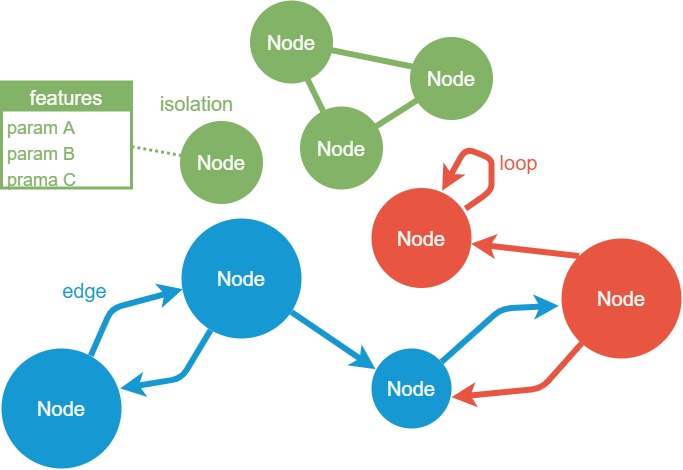
グラフの用語について簡単に整理したものが以下です。
- ノード(node):データ
- エッジ(edge):ノード間の関係、相互作用
- 有向エッジ:向きがあるエッジ
- 無向エッジ:向きがないエッジ
- 有向グラフ:有向エッジがあるグラフ
- 無向グラフ:有向エッジがないグラフ
- ループ(loop):エッジが1つのノードにしか繋がっていないもの
- 孤立ノード(isolation):ノードが孤立しているもの
- 属性:各ノードや各エッジがもつパラメータ(≒特徴量)
- ノードの位置情報:あり/なし
- ラベル:あり/なし ※
- 重み:あり/なし
※上図だと色でラベルを表現
例えば、SNSの場合は以下の通りです。
- ノード(node):人(アカウント名)
- エッジ(edge):フォロー関係(相互フォローなど)
- ノード属性:アカウント情報(生年月日など)
問題設定 -グラフと深層学習(GNN)-
グラフと深層学習(GNN)の活用により、解決できる問題(タスク)の例を紹介します。
グラフ分類
化合物の場合、グラフから毒性の有無などを分類することができます。
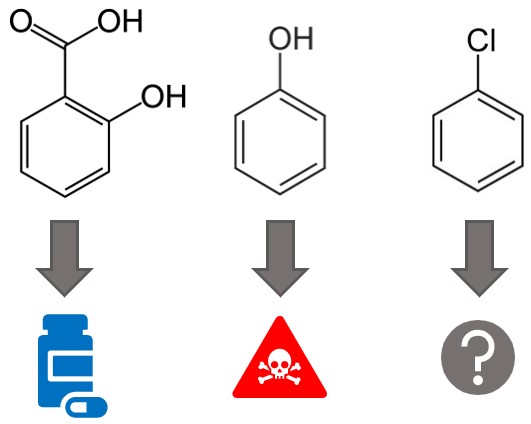
深層学習によるグラフ分類ができれば、未知の化合物に対し、毒性の有無などを予測できるようになります。
ノード分類
赤チーム・青チームで対戦するゲームの各キャラクタ相関図(グラフ)が下図だとします(所属が不明なノードはグレーで表現)。
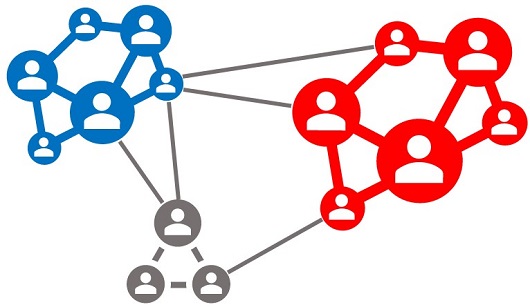
同じチーム内でも交友の有無があり、敵同士でもライバル関係などのエッジが存在します。
各ノードとエッジの情報から、グレーの所属(ラベル)を分類できれば、分類結果を考慮した戦略を検討できます(情報戦)。
このような各ノードのラベルを予測するノード分類にも深層学習が活用できます。
リンク予測
Amazonなどの購入履歴をグラフで表現したものが下図だとします。
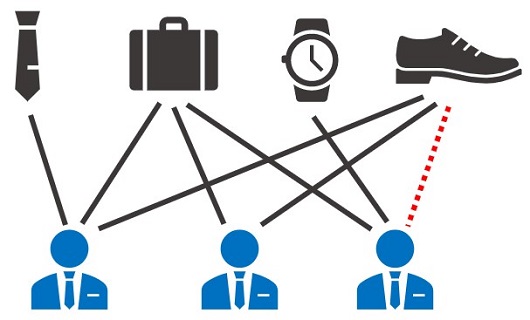
- カバン👜を購入する人は、革靴👞も一緒に購入する
- 革靴👞のページをn日間でm回以上閲覧している人は購入する
など
もし上記の関係性を予測できるなら、潜在的な顧客の発見に繋がります。このような関係性の予測(リンク予測)にも深層学習を活用できます。
本記事では分類タスクのみを紹介しましたが、回帰タスクもあります。
Graph Neural Network(GNN)とは
グラフの概要や深層学習(GNN)で解決できる問題(タスク)について説明したので、今度はGNN(主にGCN)のアルゴリズムについて説明します。
GNN・GCNについて
よくわかる Gated Graph Neural Network (GGNN)の記事で紹介している以下の動画がとても分かりやすいです。
この動画でイメージを掴んだら、次はGraph Convolutional Network(GCN)について学びます。以下の2つスライドがオススメです。
https://www.slideshare.net/ryosuke-kojima/ss-179423718
https://www.slideshare.net/ssuser0c8361/20200212-227754437?ref=https://dllab.connpass.com/event/159148/presentation/
最後に数式の意味を深く学びたい人のために、以下の記事をオススメしておきます。
Graph Neural Network(GNN)実践
各資料でGNNのアルゴリズムを勉強したので、次は実践します!
Graph Neural Network(GNN)ライブラリ
どのGNNライブラリを使うか迷ったので、Twitterのアンケート機能を使ってみました。
https://twitter.com/Cpp_Learning/status/1246038665014345729
アンケートにご回答いただき、ありがとうございました。ユーザーの多い PyTorch Geometric を使ってGNNを実践します。
インストール
メインで使用するライブラリは以下の通りです。
- PyTorch Geometric 1.4.3
- PyTorch 1.4.0
- CUDA 10.1
※Google Colaboratoryで動作確認しました(2020/04/18)
まずはGoogle Colaboratoryにプリインストールしてあるライブラリのバージョンを確認します。
|
1 2 3 4 |
import torch print("PyTorch ==", torch.__version__) print("CUDA available", torch.cuda.is_available()) print("CUDA ==", torch.version.cuda) |
PyTorch == 1.4.0
CUDA available True
CUDA == 10.1
CUDAについては以下のコマンドでも確認できます。
|
1 2 3 |
!nvcc --version |
nvcc: NVIDIA (R) Cuda compiler driver Copyright (c) 2005-2018 NVIDIA Corporation Built on Sat_Aug_25_21:08:01_CDT_2018 Cuda compilation tools, release 10.0, V10.0.130
※CUDAのバージョンに注意!
PyTorch Geometric|公式のインストール手順だと失敗するので、解決策を参考に以下のコマンドでインストールします。
|
1 2 3 4 |
!pip install torch-scatter==latest+cu101 torch-sparse==latest+cu101 -f https://s3.eu-central-1.amazonaws.com/pytorch-geometric.com/whl/torch-1.4.0.html !pip install torch-geometric |
以上でPyTorch Geometricを使う環境が準備できました。以降からソースコードを書いてきます。
PyTorch Geometricの基本的な使い方 -グラフ作成-
まずは下図の有向グラフ(ノードに属性とラベルあり)を作成してみます。
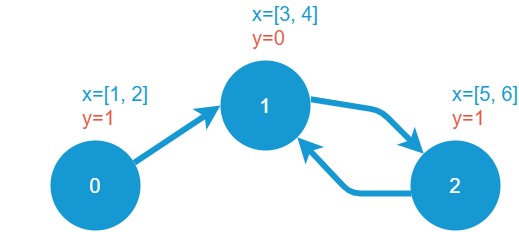
PyTorch Geometricを使えば、以下のコードで簡単にグラフを作成できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import torch from torch_geometric.data import Data # ノード src = [0, 1, 2] # 送信側 dst = [1, 2, 1] # 受信側 # エッジ edge_index = torch.tensor([src, dst], dtype=torch.long) # ノードの特徴量 x0 = [1, 2] x1 = [3, 4] x2 = [5, 6] x = torch.tensor([x0, x1, x2], dtype=torch.float) # ラベル y0 = [1] y1 = [0] y2 = [1] y = torch.tensor([y0, y1, y2], dtype=torch.float) data = Data(x=x, y=y, edge_index=edge_index) |
edge_indexでエッジを定義します。今回の場合「0⇒1, 1⇒2, 2⇒1」とメッセージを伝播させたいので、コードの4~9行目で設定しています。
各ノードの属性(特徴量)とラベルはtorch.tensorで定義します(コード 15行目、21行目)。
最後にDataモジュールでグラフを作成します(コード 23行目)。
慣れてくれば、以下のような短いコードでグラフを作成できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import torch from torch_geometric.data import Data # エッジ edge_index = torch.tensor([[0, 1, 2], [1, 2, 1]], dtype=torch.long) # ノードの特徴量 x = torch.tensor([[1, 2], [3, 4], [5, 6]], dtype=torch.float) # ラベル y = torch.tensor([[1], [0], [1]], dtype=torch.float) data = Data(x=x, y=y, edge_index=edge_index) |
今回は各ノードの特徴量とラベルを定義してますが、edge_indexだけでもグラフを生成できます
グラフ情報の確認
作成したグラフを以下の自作関数で確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def check_graph(data): '''グラフ情報を表示''' print("グラフ構造:", data) print("グラフのキー: ", data.keys) print("ノード数:", data.num_nodes) print("エッジ数:", data.num_edges) print("ノードの特徴量数:", data.num_node_features) print("孤立したノードの有無:", data.contains_isolated_nodes()) print("自己ループの有無:", data.contains_self_loops()) print("====== ノードの特徴量:x ======") print(data['x']) print("====== ノードのクラス:y ======") print(data['y']) print("========= エッジ形状 =========") print(data['edge_index']) check_graph(data) |
グラフ構造: Data(edge_index=[2, 3], x=[3, 2], y=[3, 1])
グラフのキー: [‘x’, ‘edge_index’, ‘y’]
ノード数: 3
エッジ数: 3
ノードの特徴量数: 2
孤立したノードの有無: False
自己ループの有無: False
====== ノードの特徴量:x ======
tensor([[1., 2.], [3., 4.], [5., 6.]])
====== ノードのクラス:y ======
tensor([[1.], [0.], [1.]])
======== エッジ形状 ========
tensor([[0, 1, 2], [1, 2, 1]])
ちゃんと下図のグラフを作成できてますね。

Graph Convolutional Network(GCN)実践
PyTorch Geometricによるグラフの扱い方が分かったので、今度はGCNによるノード分類を実践します。
Import
最初はimportから
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import torch import torch.nn.functional as F from torch_geometric.nn import GCNConv from torch_geometric.data import Data from torch_geometric.datasets import KarateClub # import torch_geometric.transforms as T from torch_geometric.utils import to_networkx import networkx as nx from matplotlib import pyplot as plt import numpy as np |
データセットのダウンロード
自作グラフのデータセットを作成しても良いのですが、今回はGNN界隈のMNISTに相当する空手クラブのデータセットを使います。
|
1 2 3 4 5 6 7 8 |
# データセットをダウンロード dataset = KarateClub() print("グラフ数:", len(dataset)) # グラフ数: 1 print("クラス数:",dataset.num_classes) # クラス数: 2 data = dataset[0] # 1つめのグラフ check_graph(data) |
グラフ数: 1
クラス数: 2
グラフ構造: Data(edge_index=[2, 156], x=[34, 34], y=[34])
グラフのキー: [‘x’, ‘edge_index’, ‘y’]
ノード数: 34
エッジ数: 156
ノードの特徴量数: 34
孤立したノードの有無: False
自己ループの有無: False
====== ノードの特徴量:x ======
tensor([[1., 0., 0., …, 0., 0., 0.],
[0., 1., 0., …, 0., 0., 0.],
[0., 0., 1., …, 0., 0., 0.],
…,
[0., 0., 0., …, 1., 0., 0.],
[0., 0., 0., …, 0., 1., 0.],
[0., 0., 0., …, 0., 0., 1.]])
==== ノードのクラス:y ====
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
========= エッジ形状 =========
tensor([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13, 13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 27, 27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 30, 30, 31, 31, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33],
[ 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31, 0, 2, 3, 7, 13, 17, 19, 21, 30, 0, 1, 3, 7, 8, 9, 13, 27, 28, 32, 0, 1, 2, 7, 12, 13, 0, 6, 10, 0, 6, 10, 16, 0, 4, 5, 16, 0, 1, 2, 3, 0, 2, 30, 32, 33, 2, 33, 0, 4, 5, 0, 0, 3, 0, 1, 2, 3, 33, 32, 33, 32, 33, 5, 6, 0, 1, 32, 33, 0, 1, 33, 32, 33, 0, 1, 32, 33, 25, 27, 29, 32, 33, 25, 27, 31, 23, 24, 31, 29, 33, 2, 23, 24, 33, 2, 31, 33, 23, 26, 32, 33, 1, 8, 32, 33, 0, 24, 25, 28, 32, 33, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 33, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]])
空手クラブの情報を簡単に整理すると以下の通りです。
- 会員数(ノード数):34
- 特徴量x:ノード番号(会員ナンバー)をone-hotベクトルで定義
- ラベルy:”0”または”1″の2クラス(2グループ)
- 交友関係(エッジ数):156
- グラフの種類:無向グラフ※
※各ノード間を有効エッジで相互に接続(0⇒1, 1⇒0など)することで無向グラフとして表現することがあります
グラフ構造の可視化
PyTorch Geometricにはグラフ構造を可視化する関数がないため、NetworkXを使って可視化します(ここのコードやここのコードを参考にしました)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# networkxのグラフに変換 nxg = to_networkx(data) # 可視化のためのページランク計算 pr = nx.pagerank(nxg) pr_max = np.array(list(pr.values())).max() # 可視化する際のノード位置 draw_pos = nx.spring_layout(nxg, seed=0) # ノードの色設定 cmap = plt.get_cmap('tab10') labels = data.y.numpy() colors = [cmap(l) for l in labels] # 図のサイズ plt.figure(figsize=(10, 10)) # 描画 nx.draw_networkx_nodes(nxg, draw_pos, node_size=[v / pr_max * 1000 for v in pr.values()], node_color=colors, alpha=0.5) nx.draw_networkx_edges(nxg, draw_pos, arrowstyle='-', alpha=0.2) nx.draw_networkx_labels(nxg, draw_pos, font_size=10) plt.title('KarateClub') plt.show() |
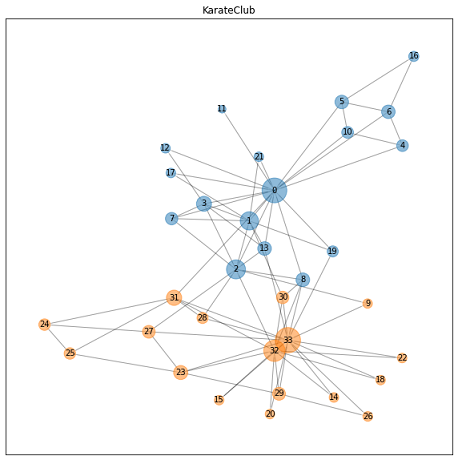
可視化によりリーダー格のノード”0”とノード”33”を中心とした2グループの存在が明確になりました。
またノード”8”やノード”9”は両グループと交友関係があることも分かります(伏線)。
この空手クラブのデータセットを使ってノード分類を実践します。
モデル設計
PyTorch Geometricは GCNConv などの メジャーなLayers をサポートしているので、ピュアPyTorchと同じ感覚でモデルを設計できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class Net(torch.nn.Module): def __init__(self): super(Net, self).__init__() hidden_size = 5 self.conv1 = GCNConv(dataset.num_node_features, hidden_size) self.conv2 = GCNConv(hidden_size, dataset.num_classes) def forward(self, data): x, edge_index = data.x, data.edge_index x = self.conv1(x, edge_index) x = F.relu(x) # x = F.dropout(x, training=self.training) x = self.conv2(x, edge_index) return F.log_softmax(x, dim=1) |
ピュアPyTorchと同じコードが使えます
各種設定
以下のコードで各種の設定を行います。
|
1 2 3 4 5 6 7 8 9 |
# デバイス設定 device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # モデルのインスタンス生成 model = Net() # print(model) # モデルを訓練モードに設定 model.train() |
学習
入力データ(入力するグラフ)、オプティマイザ設定、学習ループのコードは以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# input data data = dataset[0] # optimizer optimizer = torch.optim.Adam(model.parameters(), lr=0.01) # optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4) # learnig loop for epoch in range(100): optimizer.zero_grad() out = model(data) loss = F.nll_loss(out, data.y) loss.backward() optimizer.step() print('Epoch %d | Loss: %.4f' % (epoch, loss.item())) |
Epoch 0 | Loss: 0.6980
Epoch 1 | Loss: 0.6863
Epoch 2 | Loss: 0.6748
…
Epoch 97 | Loss: 0.0563
Epoch 98 | Loss: 0.0559
Epoch 99 | Loss: 0.0555
推論
以下のコードで推論します。
|
1 2 3 4 5 6 7 8 |
# モデルを評価モードに設定 model.eval() # 推論 _, pred = model(data).max(dim=1) print("結果:", pred) print("真値:", data[0]["y"]) |
結果: tensor([0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
真値: tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
ノード”8”を誤分類していることが分かります。
ノード”8”は両グループのリーダーと交流があるため、ラベル(所属)の判断が難しかったと考えられます
テストデータ作成
学習に未使用のテストデータでも推論してみます。空手クラブのデータセットを活用し、交友関係(リンク)を一部変更したグラフを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
test_dataset = KarateClub() test_data = test_dataset[0] x = test_data["x"] edge_index = test_data['edge_index'] # change link of ID:0, ID:2, ID:8, ID:9 and ID:33 edge_index[1][61] = 0 # 「ノード9⇒ノード2」から「ノード9⇒ノード0」にリンク変更 edge_index[1][7] = 9 # 「ノード0⇒ノード8」から「ノード0⇒ノード9」にリンク変更 edge_index[1][56] = 9 # 「ノード8⇒ノード0」から「ノード8⇒ノード9」にリンク変更 edge_index[1][62] = 8 # 「ノード9⇒ノード33」から「ノード9⇒ノード8」にリンク変更 edge_index[1][140] = 2 # 「ノード33⇒ノード9」から「ノード33⇒ノード2」にリンク変更 edge_index[1][30] = 33 # 「ノード2⇒ノード9」から「ノード2⇒ノード33」にリンク変更 t_data = Data(x=x, edge_index=edge_index) check_graph(t_data) |
変更前後のグラフは以下の通りです。

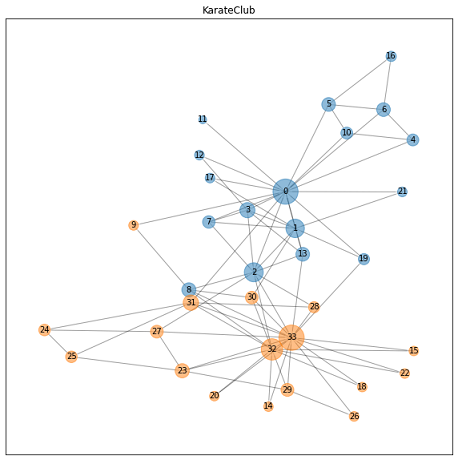
- ノード”2”とノード”33”のリンクを接続
- ノード”8”とノード”0”のリンクを切る
- ノード”9”とノード”33”のリンクを切る
- ノード”9”とノード”0”のリンクを接続
など
要するにリーダとの交友関係の有無(リンク変更)により、モデルのラベル予測(ノード分類結果)がどう変わるかを検証するために、グラフに色々と手を加えました。
- モデルがリーダとの交友関係を考慮して、ノード分類をしているか検証
- GNNとモデルの説明性に興味津々
リンク変更によるノード分類結果について
リンク変更後のグラフに対し、学習済みモデルによるノード分類(ラベル予測)を行います。
|
1 2 3 4 5 6 7 |
model.eval() #モデルを評価モードにする。 _, pred = model(t_data).max(dim=1) print(" ======== リンク変更前のラベル ======== ") print(data["y"]) print(" ==== リンク変更後のラベル予測結果 ==== ") print(pred) |
======== リンク変更前のラベル ========
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
==== リンク変更後のラベル予測結果 ====
tensor([0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
ノード分類結果を反映したグラフが下図です。

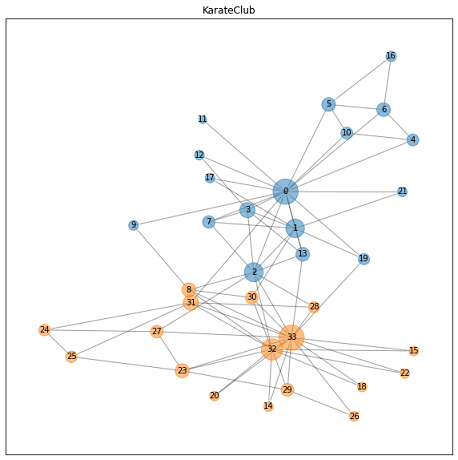
つまり今回のモデルは、以下の予測傾向があると考えられます。
- 交流のあるリーダと同じグループだと予測
- 両リーダーと交流がある場合、ノード”0”と同じグループと予測
以上 簡単な検証ですが、リンク変更による検証からGNNのモデル説明性を深堀りできそうです。
- GNN(GCN)により、ノード分類(ラベル予測)ができる
- リンク変更によりモデルのノード分類結果が変化する
- 結果の変化からモデルの予測傾向を把握できそう(モデル説明性)
- 分類結果に大きく影響を与える重要なノードを把握できそう(潜在的なリーダの予測に活用できそう)
まとめ
Graph Neural Network(GNN)の概要からPyTorch Geometricを使ったノード分類の実践などについて説明しました。
と考えている人の参考になれば嬉しいです。
また私自身もGNN入門したばかりなので、本記事の内容について間違っている箇所があれば、教えて頂けると嬉しいです。