こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
今回は確率的プログラミング言語のPyroによるベイズ統計モデリングに挑戦したので、備忘録も兼ねて本記事を書きます。
Contents
まえおき
確率的プログラミング言語については、以下の記事で説明済みなので、本記事では割愛します。
また上の記事では事後分布の算出にMCMCを使いましたが、本記事では変分推論(variational inference)を使います。
変分推論ではなく、変分近似(variational approximation)や変分ベイズ(variational Bayes)と呼ぶこともあります(以下 参考記事)。
変分推論とは
機械学習とは『モデルの出力結果と真値との距離(loss)を最小化するアルゴリズムです』と説明するなら…
変分推論とは『モデルの確率分布とデータから得られた真の確率分布間の距離(KLダイバージェンス)を最小化するアルゴリズムです』という説明ができます。
また機械学習が目的関数(MSE:平均二乗誤差 など)からの出力結果(loss)を評価指標に使うのに対し、変分推論ではELBOなどを評価指標に使います。
もっと詳しく知りたい人のために、以下の本をオススメしておきます。
実践!Pyroでベイズ回帰モデルをつくる -変分推論-
MCMCと比較できるように、以下の記事と同じ問題設定「会計総額からチップ額を予測」にベイズ回帰モデル + 変分推論を活用します。

インストール
公式サイトに従い、先にPyTorchをインストールしてください。
PyTorchがインストール済みなら、以下のコマンドで Pyro をインストールするだけでOKです。
pip install pyro-ppl
以降からコード書いていきます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns import torch import torch.distributions.constraints as constraints import pyro import pyro.distributions as dist import pyro.infer as infer from pyro.infer import SVI, Trace_ELBO from pyro.infer import Predictive from pyro.optim import Adam |
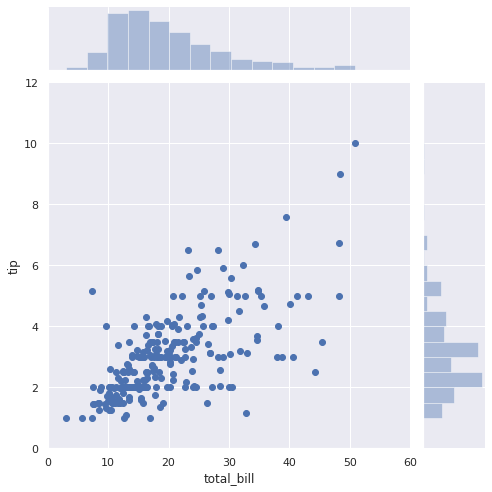
データ可視化
使用するデータを可視化します。
|
1 2 3 4 5 6 7 8 9 10 |
# チップのデータセット df = sns.load_dataset("tips") # 会計総額とチップのデータを可視化 sns.set(style="darkgrid") sns.jointplot(x="total_bill", y="tip", data=df, kind="scatter", xlim=(0, 60), ylim=(0, 12), color="b", height=7); |
説明変数と目的変数 -torch.tensorに変換–
説明変数:X と 目的変数:Y を定義します。
|
1 2 3 4 5 6 7 |
# dfからnumpy.ndarrayに変換 Y = df['tip'].values # 目的変数:Y = [y0, y1, y2, ... yi] X = df['total_bill'].values # 説明変数:X = [x0, x1, x2, ... xi] # numpy.ndarrayからtorch.tensorに変換 Yt = torch.tensor(Y, dtype=torch.float) # 目的変数:Y = [y0, y1, y2, ... yi] Xt = torch.tensor(X, dtype=torch.float) # 説明変数:X = [x0, x1, x2, ... xi] |
※PyroのバックエンドがPyTorchなので、torch.tensorを扱います
ベイズ統計モデリング -線形回帰モデル-
この記事と同じモデルを設計します。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 線形回帰モデルの設計 def model(X, Y=None): pm_a = pyro.sample('pm_a', dist.Normal(0.0, 10.0)) pm_b = pyro.sample('pm_b', dist.Normal(0.0, 10.0)) mu = pm_a * X + pm_b sigma = 1.0 pm_Y = pyro.sample('pm_Y', dist.Normal(mu, sigma), obs=Y) return pm_Y |
近似事後分布
データから得られる複雑な確率分布(以降 真の事後分布 と呼ぶ)が、簡単な確率分布(以降 近似事後分布 と呼ぶ)でも近似できると考え、以下のように近似事後分布を設計します。
|
1 2 3 4 5 6 7 8 9 |
def my_guide(X, Y): # 変分パラメータ a_mu = pyro.param('a_mu', torch.tensor(0.0)) b_mu = pyro.param('b_mu', torch.tensor(0.0)) a_sigma = pyro.param('a_sigma', torch.tensor(1.0), constraints.positive) b_sigma = pyro.param('b_sigma', torch.tensor(1.0), constraints.positive) pyro.sample('pm_a', dist.Normal(a_mu, a_sigma)) pyro.sample('pm_b', dist.Normal(b_mu, b_sigma)) |
以下のように既に準備してあるものを使うこともできます。
|
1 2 3 |
guide = infer.autoguide.guides.AutoDiagonalNormal(model) |
※今回は AutoDiagonalNormal を使います
各種設定
変分推論のインターフェースを作ります。
|
1 2 3 4 5 6 7 8 |
# 変分パラメータの辞書を空にする pyro.clear_param_store() # 最適化手法 optimizer = Adam({"lr": 0.001}) # 変分推論のインターフェース svi = SVI(model, guide, optimizer, loss=Trace_ELBO()) |
※Adamは深層学習でもお馴染みですね
変分推論
以下のコードで指定した回数だけ推論(機械学習でいう学習)を実行します。
|
1 2 3 4 5 6 |
num_iterations = 20000 # calculate the loss and take a gradient step for i in range(num_iterations): loss = svi.step(Xt, Yt) if i % 100 == 0: print("[iteration %04d] loss: %.4f" % (i + 1, loss / len(Xt))) |
[iteration 0001] loss: 4904.6740
[iteration 0101] loss: 3820.1017
[iteration 0201] loss: 4124.2043
…
[iteration 19701] loss: 1.5044
[iteration 19801] loss: 1.4919
[iteration 19901] loss: 1.4918
途中経過を割愛してますが、上記のようにlossが下がっている様子を確認できます。
これは近似事後分布と真の事後分布との距離が近くなる変分パラメータを推論できている、あるいは 真の事後分布を簡単な確率分布で近似できる変分パラメータを推論できている…といえます。
変分パラメータ取得
変分パラメータは pyro.get_param_store() に辞書型で格納されます。なので以下のコードでkeyとvalueを確認しておきます。
|
1 2 3 |
for key, value in pyro.get_param_store().items(): print(' {}: {}'.format(key, value)) |
今回は以下のコードで変分パラメータを取得できます。
|
1 2 3 4 5 6 7 8 9 |
# mu = [a_mu, b_mu], sigma = [a_sigma, b_sigma] mu = pyro.get_param_store()["AutoDiagonalNormal.loc"] sigma = pyro.get_param_store()["AutoDiagonalNormal.scale"] # 変分パラメータ a_mu = mu[0] b_mu = mu[1] a_sigma = sigma[0] b_sigma = sigma[1] |
変分パラメータの格納形式について、以下の記事が参考になりました。
事後分布の可視化
変分パラメータを使って事後分布を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
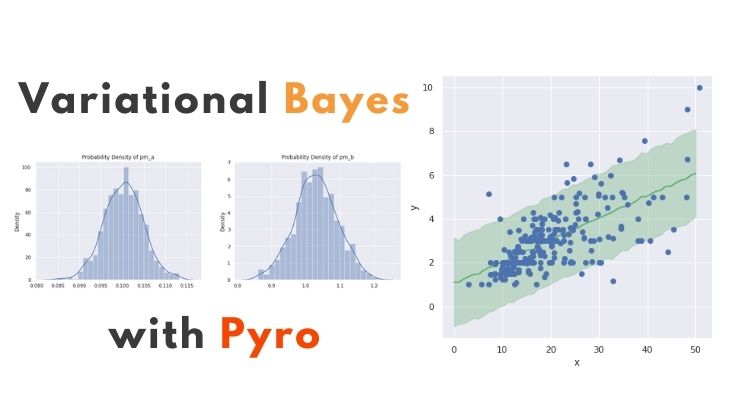
# 事後分布 pm_a = np.random.normal(a_mu.detach().numpy(), a_sigma.detach().numpy(), 1000) pm_b = np.random.normal(b_mu.detach().numpy(), b_sigma.detach().numpy(), 1000) # 可視化 sns.set(style="darkgrid") plt.figure(figsize=(15, 5)) plt.subplot(1, 2, 1) sns.distplot(pm_a) plt.title("Probability Density of pm_a") plt.subplot(1, 2, 2) sns.distplot(pm_b) plt.title("Probability Density of pm_b") plt.show() |
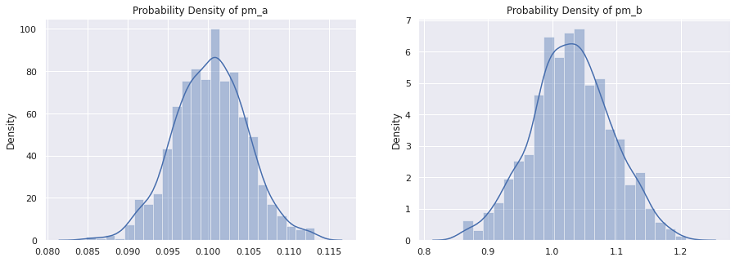
推論
以下のコードで X=0, 1, …, 49, 50 のときの Y を予測します。
|
1 2 3 4 5 6 7 8 |
X_range = torch.tensor(np.linspace(0, 50, 50)) predictive = Predictive(model=model, guide=guide, num_samples=1000, return_sites=["pm_Y"]) predict_samples = predictive.get_samples(X_range, None) # print(predict_samples.items()) pm_Y = predict_samples['pm_Y'] print(pm_Y) |
以下のコードで予測結果を可視化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
mean_Y = predict_samples['pm_Y'].mean(0).detach() std_Y = predict_samples["pm_Y"].std(0).detach() y_low = mean_Y - std_Y * 2 y_high = mean_Y + std_Y * 2 # 可視化 fig = plt.figure(figsize=(6.0, 6.0)) plt.plot(X_range, mean_Y, '-', color='g') plt.fill_between(X_range, y_low, y_high, color='g', alpha=0.3) plt.plot(X, Y, "o") plt.xlabel('x'), plt.ylabel('y') plt.show() |
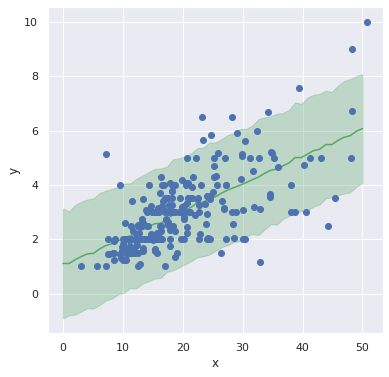
今回はMCMCとほとんど同じ結果が得られました。
【おまけ】ベイズ回帰やるなら、どの手法を使う?
本記事を書く前に以下のアンケートを行いました。
https://twitter.com/Cpp_Learning/status/1320190510141640704
回答してくれた人ありがとうございました。MAP推定を使っている人や…
と考えて、回答に悩んだ人がいたら、ごめんなさい。
変分推論 ユーザーは少ないようですが、本記事が参考になれば嬉しいです。
まとめ -変分ベイズ入門-
ベイズ統計モデリングについて勉強し、Pyroで実践(変分推論)した内容をまとめました。
本記事の内容について間違っている箇所があれば、教えて頂けると嬉しいです。
以下 本記事の前半で紹介した書籍を改めてオススメしておきます。