こんにちは。現役エンジニアの”はやぶさ”@Cpp_Learningです。
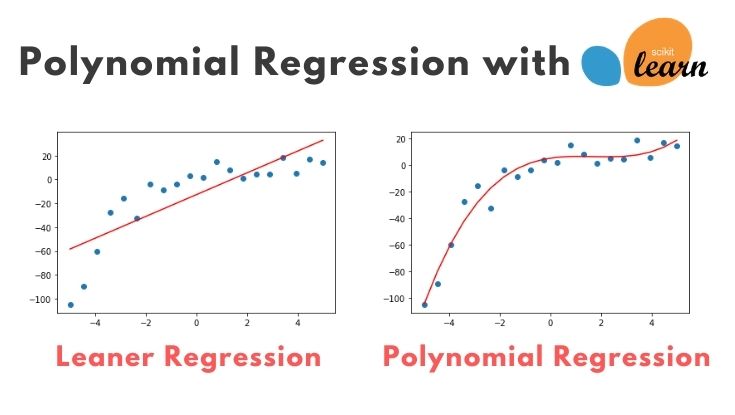
多項式回帰(Polynomial Regression)を実践するときに、sklearnのPolynomialFeaturesがとても便利だったので、使い方を紹介します。
- 線形回帰(Linear Regression)では上手くフィットしなかった
- 多項式回帰(Polynomial Regression)にトライ
- モデリング自動化とオーバーフィットについて
Contents
実践!sklearnで線形回帰
回帰とは?については下記で説明済みのため、本記事では割愛します。
以降からソースコードを交えて説明します。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 |
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error, r2_score from sklearn.preprocessing import PolynomialFeatures np.random.seed(0) |
データセット作成
適当なデータセットを作成します。
|
1 2 3 4 5 6 |
x = np.linspace(-5, 5, 20) y = 2 * x - 2 * (x ** 2) + 0.5 * (x ** 3) + np.random.normal(loc=0, scale=10, size=len(x)) # [a,b,c,..] to [[a], [b], [c]] x = x[:, np.newaxis] y = y[:, np.newaxis] |
今回は3次式にノイズを加えたデータにしました。
実際の問題では、データがどんな数式に従うのか不明なので、データにフィットする数式モデルを検討することが重要です。
線形回帰(Linear regression)
初手では線形回帰モデルを適用してみます。つまり 一次式:y = b0 + b1x がデータにフィットすると考え、機械学習でパラメータ b0, b1 を推定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# モデル:y = b0 + b1x の b0 と b1 を算出 model = LinearRegression() model.fit(x, y) # 推論 y_pred = model.predict(x) # 評価 rmse = np.sqrt(mean_squared_error(y, y_pred)) r2 = r2_score(y, y_pred) print(f'rmse : {rmse}') print(f'R2 : {r2}') # 可視化 plt.scatter(x, y) plt.plot(x, y_pred, color='r') plt.show() |
rmse : 19.313677119446293
R2 : 0.672751565398112
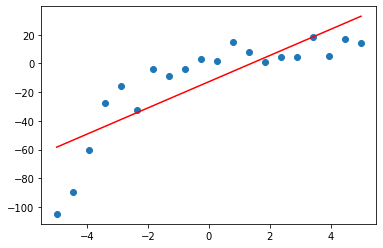
「RMSE と R2 の評価」と「データと線形回帰モデルの関係」を確認したものが上記です。
RMSE や R2 などの評価指標については、以下の記事が参考になります。
実践!sklearnで多項式回帰(2次)
y = b0 + b1x では上手くいかなかったので、 y = b0 + b1x + b1x^2 の多項式を採用します。
scikit-learnのPolynomialFeatures
scikit-learnのPolynomialFeaturesを使えば、簡単に多項式や交互作用の特徴量を生成できます。
例えば degree=2 をセットすると、特徴量 X を以下のように変換してくれます。
【origin】
X = [[x1], [x2], [x3]]
【transform】
X = [[1, x1, x1^2], [1, x2, x2^2], [1, x3, x3^2]]
あとは先ほど同様、多項式:y = b0 + b1x + b2x^2 のパラメータ b0~b2 を機械学習で推定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
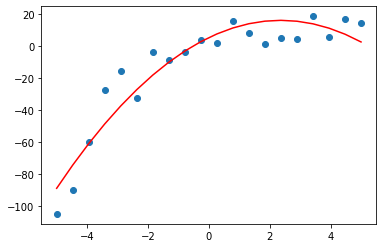
# 2次元の特徴量に変換 polynomial_features= PolynomialFeatures(degree=2) x_poly = polynomial_features.fit_transform(x) # y = b0 + b1x + b2x^2 の b0~b2 を算出 model = LinearRegression() model.fit(x_poly, y) y_pred = model.predict(x_poly) # 評価 rmse = np.sqrt(mean_squared_error(y, y_pred)) r2 = r2_score(y, y_pred) print(f'rmse : {rmse}') print(f'R2 : {r2}') # 可視化 plt.scatter(x, y) plt.plot(x, y_pred, color='r') plt.show() |
rmse : 11.007765829915302
R2 : 0.8936968806347743
実践!sklearnで多項式回帰(3次)
最後に degree=3 を試してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 3次元の特徴量に変換 polynomial_features= PolynomialFeatures(degree=3) x_poly = polynomial_features.fit_transform(x) # y = b0 + b1x + b2x^2 + b3x^3 の b0~b3 を算出 model = LinearRegression() model.fit(x_poly, y) y_pred = model.predict(x_poly) # 評価 rmse = np.sqrt(mean_squared_error(y, y_pred)) r2 = r2_score(y, y_pred) print(f'rmse : {rmse}') print(f'R2 : {r2}') # 可視化 plt.scatter(x, y) plt.plot(x, y_pred, color='r') plt.show() |
rmse : 7.304125160357986
R2 : 0.9531958828956855
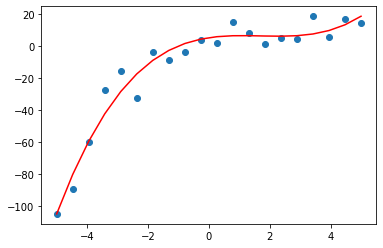
データセットを3次式から作成したので、degree=3 が高評価なのは明らかですね。
推定パラメータ取得
機械学習で推定したパラメータ b0~bn は 以下のコードで取得できます。
|
1 2 3 4 5 6 7 8 9 |
# y = b0 + b1 * x + b2 * x ** 2 + b3 * x ** 3 b0 = model.coef_[0, 0] b1 = model.coef_[0, 1] b2 = model.coef_[0, 2] b3 = model.coef_[0, 3] intercept = model.intercept_[0] print("data: y = 0.0 + 2x - 2x^2 + 0.5x^3 + random.normal") print(f'model: y = {b0} + {b1}x + {b2}x^2 + {b3}x^3 + {intercept}') |
どんな出力結果になるかは、手を動かして確認してみてください。
モデリング自動化とオーバーフィット
今回のデータセットについては degree=3 の多項式モデルを採用するのがベストでした。
ただし、以下のポイントを繰り返し明示しておきます。
実際の問題ではデータがどんな数式に従うのか不明なので、データにフィットする数式モデルを検討することが重要です。
例えば、事前に運動方程式を立て、それを数式モデルに採用し、機械学習などでパラメータ推定を自動化するのがベストだと考えています。
ただし、何らかの理由で数式モデルを事前に検討できない場合は、以下の方法で数式モデルの検討も含めて自動化できる見込みがあります。
- degree を少しづつ増やし、R2などの評価を確認(※1)
- R2 > 0.9 となる degree (多項式) を採用(※2)
(※1)どの評価指標を採用すべきかはユーザー判断
(※2)閾値についてもユーザー判断
「degree を 1~20まで振ったとき、最も評価が高かった degree (多項式) を採用」とすると、失敗するので要注意!
ソースコードは割愛しますが、degree=20 のときの結果が以下です。評価は高いものの、明らかなオーバーフィットとなります。
rmse : 0.009193268722323728
R2 : 0.9999999258540295
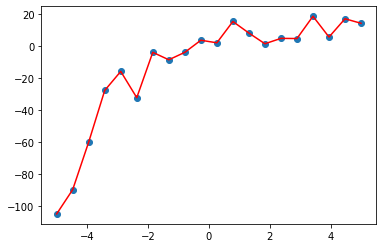
機械学習は手段なので、ユーザー判断で適切に活用しましょう。
まとめ
多項式回帰(Polynomial Regression)の入門から実践までを説明しました。
- 線形回帰と多項式回帰の比較
- sklearnのPolynomialFeaturesの使い方
- 多項式回帰とオーバーフィットに関する注意点
上記について学べる記事なので、参考になれば嬉しいです。
多項式回帰の次のステップとしては、一般化線形モデル(GLM)を学ぶのがオススメです。良ければ以下の記事を参考にしてください。

※GLMでは「数式モデルだけでなく、データがどんな分布に従うか」まで検討します
本ブログでは、多くの技術記事を無料で公開しています。Twitterで公開速報を出すので、良ければ @Cpp_Learning をフォローしたり、お友達にも教えてあげて下さい。