こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。仕事でもプライベートでも機械学習で色々やってます。
今回は次元低減の各手法を比較したので、備忘録も兼ねて本記事を書きます。
Contents
モチベーション
高次元データを扱う場合、UMAPのみで次元削減するのではなく、PCAで次元削減⇒UMAPで次元削減するのが有効とのこと。
次元削減手法(PCA+UMAPなど)を組み合わせるとか考えたこともなかった。
元データの次元にもよるけど、どの手法でどれだけ次元削減すべきか把握できるだろうか？🤔 https://t.co/zSpvH0Mm8J
— はやぶさ (@Cpp_Learning) September 4, 2020
そもそも複数の次元削減手法を組み合わせるという発想がなかったので、新鮮に感じたと同時に…
というのが気になったので、簡単な比較をしてみました。
実践！PythonでUMAP, PCA, t-SNE, “PCA & UMAP”を比較
以降からUMAP, PCA, t-SNE, “PCA & UMAP”の次元削減手法を実装していきます。
データセット
高次元かつ他の人も入手しやすいデータセットが load_digits（手書き数字の画像）しか思いつかなかったので、それを使います。
データセット可視化
一応データセットを可視化してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def plot_gallery(images, labels, h=8, w=8, n_row=2, n_col=4): """Helper function to plot a gallery of portraits""" plt.figure(figsize=(1.4 * n_col, 2.0 * n_row)) plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35) for i in range(n_row * n_col): plt.subplot(n_row, n_col, i + 1) plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray) plt.title(labels[i], size=16) plt.xticks(()) plt.yticks(()) # 数枚を可視化 plot_gallery(x_test, y_test) |
こんな感じの0~9の手書き数字データセットです。
t-SNEによる次元削減から可視化まで
本ブログでもお馴染みの t-SNE は以下のように関数化して使い回しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def plot_tsne(x, y, colormap=plt.cm.Paired): '''Visualize features with t-SNE''' plt.figure(figsize=(8, 6)) # clean the figure plt.clf() tsne = TSNE(n_components=2, random_state=0, perplexity=5) # tsne = TSNE(n_components=2, random_state=0, perplexity=5, metric="cosine") x_embedded = tsne.fit_transform(x) plt.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=colormap) plt.colorbar() plt.title("Embedding Space with t-SNE") plt.show() # Visualize features plot_tsne(x_train, y_train, 'Spectral') |
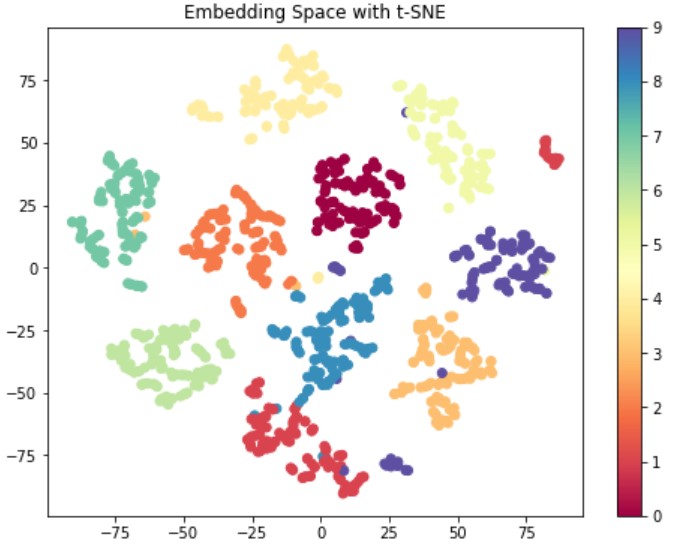
64次元のデータ（画像）を2次元に圧縮して空間に埋め込んだものが上図です。
0~9の10classあり、同じクラス同士の距離が近く、異なるクラス同士の距離が遠い空間を生成できました。つまり、t-SNEによりクラスタリング容易な埋め込み空間を生成できたといえます。
PCAによる次元削減から可視化まで
さきほどの関数を少し変更するだけで、別の次元削減手法を試せます。以下はPCAのコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def plot_pca(x, y, colormap=plt.cm.Paired): '''Visualize features with PCA''' plt.figure(figsize=(8, 6)) # clean the figure plt.clf() pca = PCA(n_components=2, random_state=0) x_embedded = pca.fit_transform(x) plt.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=colormap) plt.colorbar() plt.title("Embedding Space with PCA") plt.show() # Visualize features plot_pca(x_train, y_train, 'Spectral') |
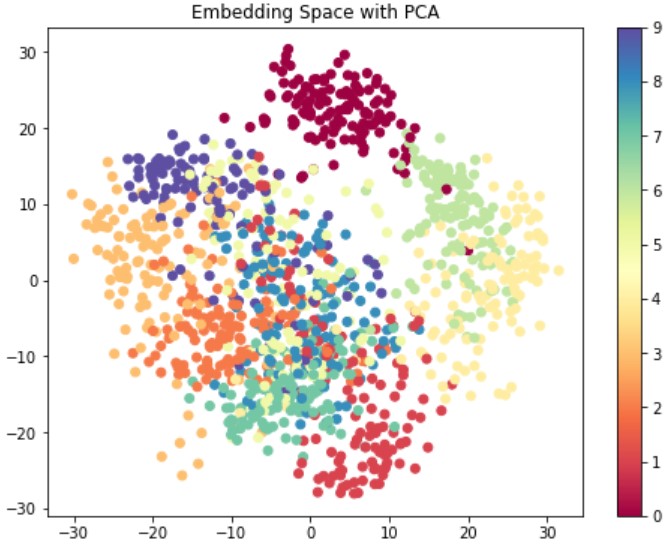
t-SNEと比べるとクラスタリングしにくい埋め込み空間といえます。（この図を見せられて「クラスを分類する境界線を引いて」と言われても困りますよね？）
UMAPによる次元削減から可視化まで
もう分かると思うけど、今まで使ってきた関数の8行目を変更するだけで、UMAPも試せます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def plot_umap(x, y, colormap=plt.cm.Paired): '''Visualize features with UMAP''' # 略 umap = UMAP(n_components=2, random_state=0, n_neighbors=5) # umap = UMAP(n_components=2, random_state=0, n_neighbors=5, metric="cosine") x_embedded = umap.fit_transform(x) # 略 plt.title("Embedding Space with UMAP") plt.show() # Visualize features plot_umap(x_train, y_train, 'Spectral') |
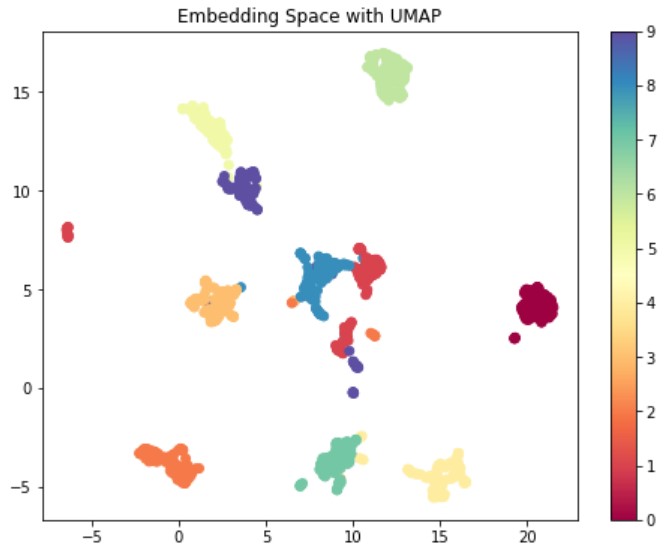
t-SNEよりもコンパクトにまとまった埋め込み空間を生成できました。これもクラスタリングしやすい良い空間だと思います。
“PCA & UMAP”による次元削減から可視化まで
本題の”PCA & UMAP”による次元削減をしてみます。Twitter経由でPCAで50次元に圧縮するのが良いかも（？）という情報を頂きました。
In many t-SNE applications, a value of 50 is recommended, although there’s no guarantee that this is appropriate for all settings.
ただ、今回は64次元のデータなので、50次元だとあまり圧縮できません。なので、とりあえずPCAで元データを2/3（40次元）に圧縮してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def plot_pca_umap(x, y, colormap=plt.cm.Paired): '''Visualize features with PCA''' plt.figure(figsize=(8, 6)) # 略 pca = PCA(n_components=40, random_state=0) umap = UMAP(n_components=2, random_state=0, n_neighbors=5) pca_x = pca.fit_transform(x) x_embedded = umap.fit_transform(pca_x) # 略 plt.title("Embedding Space with PCA and UMAP") plt.show() # Visualize features plot_pca_umap(x_train, y_train, 'Spectral') |
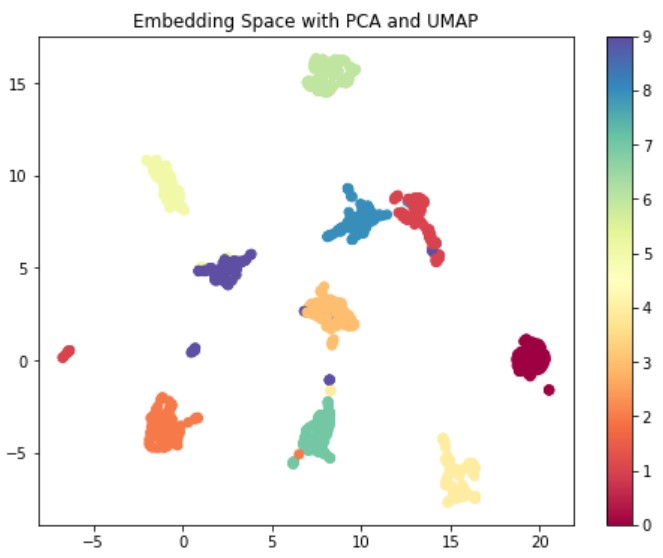
- 64次元の入力データをPCAで40次元に圧縮
- さらにUMAPで2次元に圧縮
UMAP単体より、少しだけ良い埋め込み空間を生成できた気がします。
主成分分析（PCA）と累積寄与率
PCAでn次元に圧縮したとき、第1主成分（PC1）から第n主成分（PCn）が存在します。
また各主成分の寄与率（元データの情報が何%含まれているか）を算出し、累積寄与率80%の主成分までを使うのが良いようです。
|
1 2 3 4 5 |
plt.plot(np.cumsum(pca.explained_variance_ratio_), '-o') plt.xlabel("principal components(PC1, PC2, .., PC39, PC40)") plt.ylabel("cumulative contribution rate") plt.grid() plt.show() |
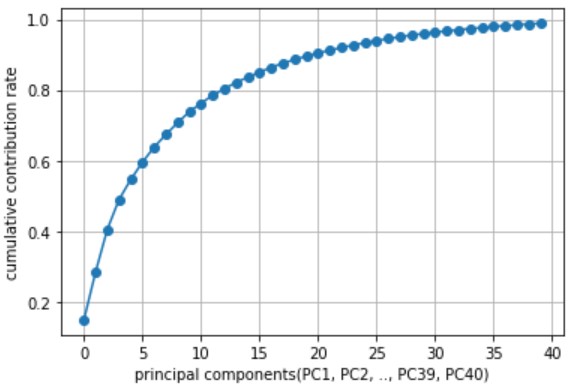
上図を参考に第13成分（PC13）までを使い、改めて”PCA & UMAP”による次元削減をした結果が以下です。
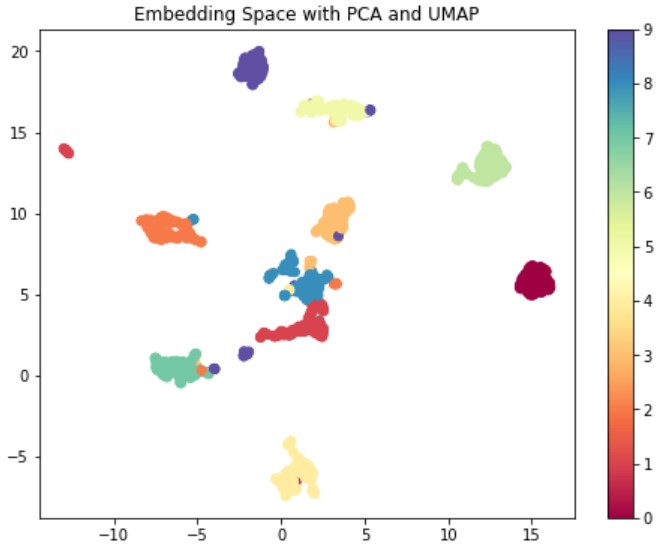
PCA13＆UMAPがPCAで元データ（64次元）を13次元に圧縮し、さらにUMAPで2次元に圧縮した結果です。
今回の場合、PCAで元データを2/3（40次元）に圧縮した埋め込み空間が最もクラスタリングしやすい（パッと見で境界線を引けそうな）結果だと感じました。
おわりに
複数の次元削減手法を組み合わせることで、クラスタリング容易な埋め込み空間を生成できるのか？というのが気になり、各手法を簡単に比較してみました。
今回扱った64次元のデータ（画像）の場合、”PCA＆UMAP”の組み合わせが僅差で良い結果だと感じました。ただし、以下の点が検証不足です。
- 画像以外のデータの場合はどうなる？
- もっと高次元のデータの場合は？
- あるいはもっと低次元のデータの場合は？
- PCA以外の手法とUMAPを組み合わせた場合は？
など
各種検証した結果をまとめたら面白そうだなぁと思いつつ、一人で実践するのは非常に時間がかかりそうなので、ここで終わります。
本記事をきっかけに、次元削減手法の組み合わせに興味をもった人が現れたら嬉しいです。また何らかの検証を行い、情報共有してくれたら最高に嬉しいです。
ディープラーニングで埋め込み空間を生成する手法（深層距離学習）も面白いよ。
