こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近、距離学習を楽しく勉強しています。
今回は、損失関数のCenter Lossについて勉強したので、備忘録も兼ねて本記事を書きます。
Contents
深層距離学習(Deep Metric Learning)とは
深層距離学習の概要については、以下の記事で説明済みなので割愛します。
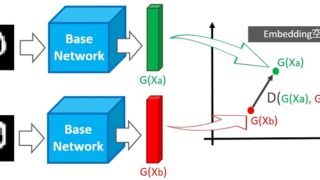
また、以降の説明でSiamese Network(以下 Siamese)との比較もするので、先にSiamese記事を読むと、本記事の内容を効率よく理解できます。
分類問題の課題
クラスタリング・異常検出・画像分類などを実践すると簡単なサンプルと難しいサンプルがあることに気づくと思います。
感覚的にも、人と犬の分類は簡単でフクロウと猫の分類は難しいと思いませんか?
 出典:TensorFlowの学習済みモデルを変換してONNXRuntimeで物体検出|はやぶさの技術ノート
出典:TensorFlowの学習済みモデルを変換してONNXRuntimeで物体検出|はやぶさの技術ノート
という声が聞こえてきそうですが、人の顔を分類(見分ける)って難しいと思いませんか?
簡単なサンプルと難しいサンプル
ここまでの説明で感覚的に簡単なサンプルと難しいサンプルがあり、特に顔認識(Face Recognition)は難しいことを理解して頂けたら嬉しいです。
ここからは、なぜ顔認識が難しいのかを説明します。
上記の距離学習(Metric Learning)記事で、特徴量を空間に埋め込めると説明しました。埋め込み手法(次元削減)については後で説明するとして、画像も空間に埋め込むことができます。
ここでいう画像をAさん・Bさん・Cさんの顔写真と考え、埋め込み空間(Embedding Space)を生成したものが下図だとします。
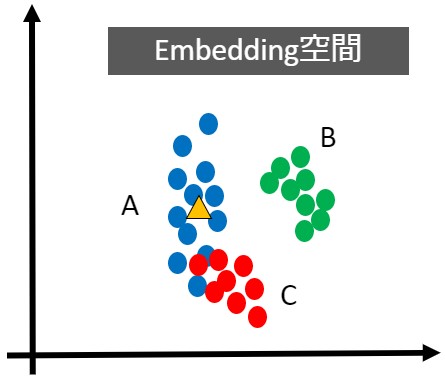
同じAさんでも髪型や化粧で雰囲気(特徴)が変わったり、横顔がCさんに似ているなどのケースが考えられます。
つまり、Aさんの顔写真を複数準備して空間に埋め込むと、全てが同じ座標というわけではなく、上図の青色プロットのような分布ができます。
同様にBさん・Cさんも分布ができ、AさんとCさんの横顔を埋め込んだ座標は距離が近くなります。「距離が近い=特徴が似ている(同じ)」という意味なので、分類困難です。
改めて図を見てみると、Aさん・Cさんの分布は距離が近いため分類が困難といえます。一方、AさんとBさんの分布は距離が離れているため、分類が簡単といえます(サンプル数を増やすとAさんとBさんの分類も困難になる可能性があります)
- 分類が難しいサンプル=距離が近い
- 分類が簡単なサンプル=距離が遠い
距離学習の課題
距離学習を活用すれば、最適な距離(あるいは最適な埋め込み空間)を学習できます。
下図が最適な距離(最適な埋め込み空間)のイメージです。
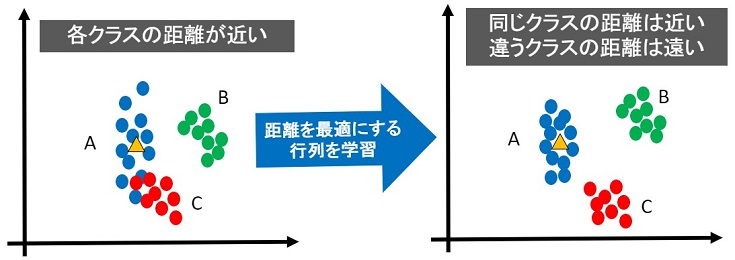
上図のように綺麗に分離できれば、精度の良い分類ができます。ただし、以下のようなサンプルではどうでしょう?
深層距離学習のSiameseは、伸びた”ばね”が縮むように同じクラスの距離を近づけ、縮んだ”ばね”が伸びるように違うクラスの距離を遠くすることで最適な距離を実現します。
しかし、上図のように各サンプルの距離が近い場合、最適な距離で”ばね”が平衡状態にならない可能性があります。
また、Contrastive Loss関数を使用するには、ペア画像のラベル付けが必要です。そのため、分類したいクラスが多い場合、ペアの組み合わせが非常に多くなるという問題があります。
このような問題をCenter Loss関数で解決します。
深層距離学習(Deep Metric Learning)の効果
Center Lossの詳細説明をする前に、深層距離学習(Deep Metric Learning)の効果について説明します。ただし、前知識として深層学習と次元削減について理解していた方が良いので、1つずつ順番に説明していきます。
深層学習と次元削減
多次元データを可視化する場合、PCAやt-SNEにより、データを2次元に圧縮することで2D空間に埋め込み可視化することができます。
ニューラルネットワークも入力データの次元削減(データ圧縮)をしています。
例えば、深層学習のCNNを用いた画像分類(データセットMNIST)の場合、28×28サイズの画像をCNNに入力し、10次元ベクトルが出力されます。これは各層で次元削減した結果、最終的には28×28サイズのデータを10次元ベクトルに圧縮したことになります。
もし、ニューラルネットワークのどこかで2次元の特徴ベクトルを出力する層があったとします。その特徴ベクトルを2D空間に埋め込めば、可視化できます。
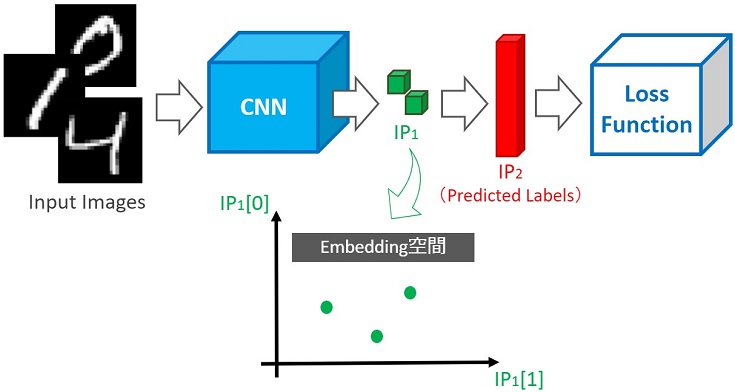
上図の例では、CNNから出力された2次元の特徴ベクトルを空間に埋め込み可視化しています。
この2次元特徴ベクトルはFC層(Fully Connected layer)に入力され、推定結果が10次元ベクトルで出力されます。さらに、10次元ベクトルはLoss関数で演算・評価され、ニューラルネットワークの重みを更新(学習)することで、分類精度を向上させていきます。
ニューラルネットワーク構造の工夫で分類精度が向上できる点については一旦置いておいて…
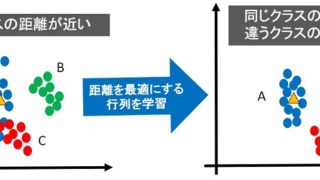
ここで注目したいのは、可視化した2次元特徴ベクトルの距離が最適な空間(綺麗に各クラスが分離され、クラスタリング容易な空間)の方が、精度の良い分類を行える点です。
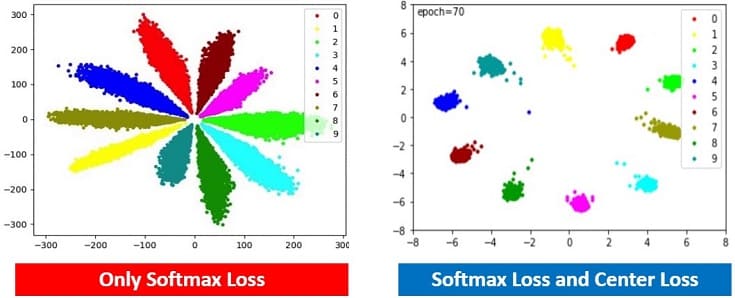
つまり、上図の左よりも右の方が精度の良い分類ができます。
深層距離学習(Deep Metric Learning)の狙い
深層学習により、次元削減が行われ、埋め込み空間を生成できることを説明しました。

しかし、必ずしも分類が容易な埋め込み空間が生成できるわけではありません。そこで、深層距離学習(Deep Metric Learning)を使い、距離が最適な埋め込み空間(Embedding Space)を生成することで、分類精度を向上させる狙いがあります。
深層距離学習のSiameseでは、ペア画像を入力するネットワーク構造とContrastive Loss関数により、最適な埋め込み空間を生成していました。
出典:A Discriminative Feature Learning Approach for Deep Face Recognition
今回は、ペア画像用のラベル付けは必要なく、従来のCNNとSoftmax LossにCenter Lossを組み込むだけで、最適な埋め込み空間を生成できます。
Center Lossとは
既に説明済みですが、Center Lossを使うことで、各クラスの距離が最適な埋め込み空間(各クラスの分類が容易な埋め込み空間)を生成できます。
以降からCenter Lossが「どうやって距離が最適な埋め込み空間を実現しているか?」のアルゴリズム詳細を説明します。
従来のSoftmax Loss関数を使った分類
深層学習による画像分類では、Softmax Loss関数が使われます。
【Softmax Loss関数】
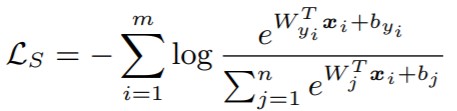
m:ミニバッチサイズ, W:重み, b:バイアス, Xi:CNNの出力特徴ベクトル
よく使われるのでSoftmaxの説明は不要だと思いますが、分類誤差を算出しています。

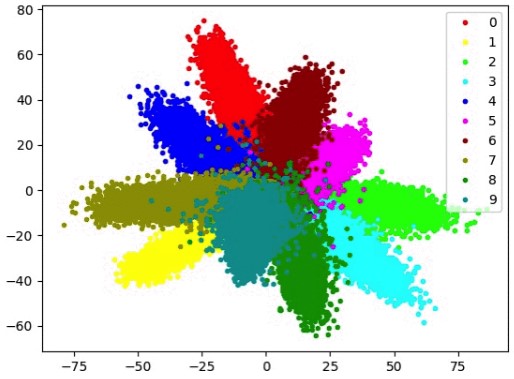
MNISTの分類にSoftmax Loss関数を使い、埋め込み空間を可視化したものが上図(左)です。綺麗に分離できているように見えますが、Center Loss関数を使った方がより良い埋め込み空間を生成できています。
Center Loss関数による最適な埋め込み空間の生成
以下の式がCenter Loss関数です。
【Center Loss関数】
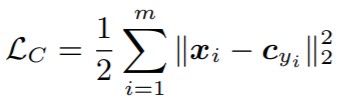
m:ミニバッチサイズ, Cyi:各クラスyの中心, Xi:CNN出力の特徴ベクトル
MSE(平均二乗誤差)に似ていますが、1/mではなく1/2を使います(条件分岐のないHuber Loss関数という説明の方が適切かな?)
1/2を使う理由は微分すると綺麗に消えて都合が良いからでしょう(下記参照)
【Center Loss関数の微分】
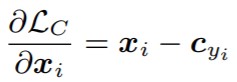
Cyi:各クラスyの中心, Xi:CNN出力の特徴ベクトル
深層学習では、Lossを最小化(最適化)するために学習を行います。つまり、各クラスの中心Cyiと各特徴ベクトルXiの距離を最小化(最適化)するために学習を行います。
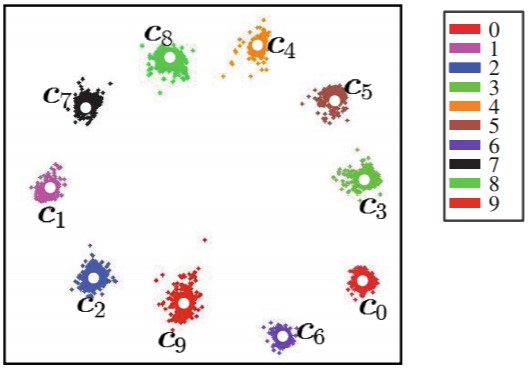
出典:A Discriminative Feature Learning Approach for Deep Face Recognition
と思ったかもしれません。Center Lossの面白いのところは、下記の式で中心Cjを更新する点です。
【Updata Center関数】
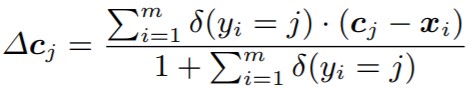
※δ(yi=j) = 1 または δ(yi=j) = 0
j:クラスid, α:ハイパーパラメータ, Cj:ミニバッチ毎の各クラスの中心
MNISTの場合、クラスidが0~9まであります。つまり、j=0~9まであります。もし、j=2の中心移動量ΔC2を算出するなら、Yi=j=2の条件を満たすときのみ演算します。
例えば、ミニバッチの入力データの内、4つのデータがYi=j=2の条件を満たす場合、空間に埋め込んだ4つの特徴ベクトルX1~X4と中心C2のみから移動量ΔC2を算出します。
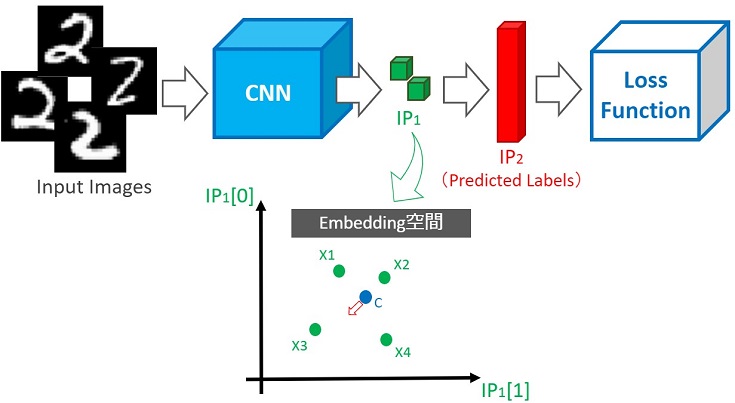
上図の中心Cですが、少し左下に移動させた方が、より最適だと思いませんか?この移動を実現するアルゴリズムについて説明します。
中心更新アルゴリズム
まず最初に、各特徴ベクトルと中心までの距離ベクトルD1~D4を算出します。
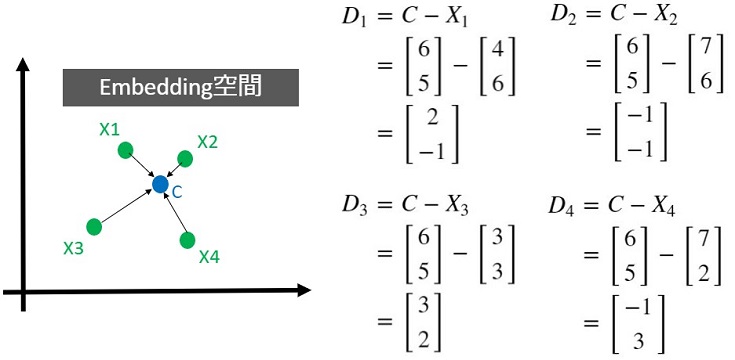
上図を見てみると距離ベクトルD3が比較的大きいことが分かります。つまり、中心Cを左下に移動(X3に近づく方向に移動)させた方が、良いと考えられます。

各距離ベクトルD1~D4を合計し、5(=1+距離ベクトル数)で割ったものが移動量ΔCです。中心更新の関数を噛砕いて書き直したものが以下です。
【Updata Center関数】
移動後の中心C = 移動前の中心C – α*ΔC
ハイパーパラメータαで移動量を調整できます。例えばα=1としたとき、各軸で-0.6移動(X3に近づく方向に移動)できることが分かります。
以上のアルゴリズムでミニバッチ毎に各クラスの中心を更新していきます。
Softmax LossとCenter Loss関数を使った分類
改めて、ネットワーク構造と損失関数(Loss関数)を確認してみます。
出典:A Discriminative Feature Learning Approach for Deep Face Recognition
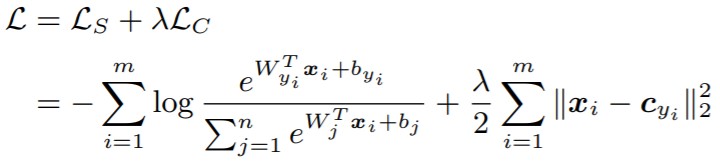
λ:ハイパーパラメータ
深層学習により、Softmax Lossで分離誤差を最小化(最適化)しつつ、Center Lossで最適な埋め込み空間を生成しています。
また、先ほど説明した通り、中心はミニバッチ毎に更新しています。
最後にハイパーパラメータのλについてですが、Center Lossの影響を調整するのに使います(下図参照)
出典:A Discriminative Feature Learning Approach for Deep Face Recognition
実践!深層距離学習 -Center Loss編-
理論の説明はここまでにして、次は実践しましょう!”ググると”以下のソースコードを見つけることができました。
論文に忠実で綺麗なコードはChainer実装ですが、Chainerは開発停止しましたね…ありがとうChainer(´;ω;`)
論文のCenter Lossを少しアレンジしていますが、今回はMNIST_center_loss_pytorchのコードを解説しながら実践していきます。
以降で説明するソースコードはGoogle Colaboratoryで動作確認しました。
import
最初はimportから
|
1 2 3 4 5 6 7 8 9 10 11 |
import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import torch.optim.lr_scheduler as lr_scheduler # from CenterLoss import CenterLoss from torch.autograd.function import Function import matplotlib.pyplot as plt |
8行目をコメントアウトしているのは、本記事のコードをGoogle Colaboratoryに写経すれば簡単に実践できる形に修正したためです。
ニューラルネットワーク設計
次にCNNを設計します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
class Net(nn.Module): def __init__(self): super(Net, self).__init__() self.conv1_1 = nn.Conv2d(1, 32, kernel_size=5, padding=2) self.prelu1_1 = nn.PReLU() self.conv1_2 = nn.Conv2d(32, 32, kernel_size=5, padding=2) self.prelu1_2 = nn.PReLU() self.conv2_1 = nn.Conv2d(32, 64, kernel_size=5, padding=2) self.prelu2_1 = nn.PReLU() self.conv2_2 = nn.Conv2d(64, 64, kernel_size=5, padding=2) self.prelu2_2 = nn.PReLU() self.conv3_1 = nn.Conv2d(64, 128, kernel_size=5, padding=2) self.prelu3_1 = nn.PReLU() self.conv3_2 = nn.Conv2d(128, 128, kernel_size=5, padding=2) self.prelu3_2 = nn.PReLU() self.preluip1 = nn.PReLU() self.ip1 = nn.Linear(128*3*3, 2) self.ip2 = nn.Linear(2, 10, bias=False) def forward(self, x): x = self.prelu1_1(self.conv1_1(x)) x = self.prelu1_2(self.conv1_2(x)) x = F.max_pool2d(x,2) x = self.prelu2_1(self.conv2_1(x)) x = self.prelu2_2(self.conv2_2(x)) x = F.max_pool2d(x,2) x = self.prelu3_1(self.conv3_1(x)) x = self.prelu3_2(self.conv3_2(x)) x = F.max_pool2d(x,2) x = x.view(-1, 128*3*3) ip1 = self.preluip1(self.ip1(x)) ip2 = self.ip2(ip1) return ip1, F.log_softmax(ip2, dim=1) |
ip1が空間に埋め込まれ、かつCenter Lossにより演算される特徴ベクトルです。
Center Loss関数
Center Loss関数を自作します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
class CenterLoss(nn.Module): def __init__(self, num_classes, feat_dim, size_average=True): super(CenterLoss, self).__init__() self.centers = nn.Parameter(torch.randn(num_classes, feat_dim)) self.centerlossfunc = CenterlossFunc.apply self.feat_dim = feat_dim self.size_average = size_average def forward(self, label, feat): batch_size = feat.size(0) feat = feat.view(batch_size, -1) # To check the dim of centers and features if feat.size(1) != self.feat_dim: raise ValueError("Center's dim: {0} should be equal to input feature's \ dim: {1}".format(self.feat_dim,feat.size(1))) batch_size_tensor = feat.new_empty(1).fill_(batch_size if self.size_average else 1) loss = self.centerlossfunc(feat, label, self.centers, batch_size_tensor) return loss class CenterlossFunc(Function): @staticmethod def forward(ctx, feature, label, centers, batch_size): ctx.save_for_backward(feature, label, centers, batch_size) centers_batch = centers.index_select(0, label.long()) return (feature - centers_batch).pow(2).sum() / 2.0 / batch_size @staticmethod def backward(ctx, grad_output): feature, label, centers, batch_size = ctx.saved_tensors centers_batch = centers.index_select(0, label.long()) diff = centers_batch - feature # init every iteration counts = centers.new_ones(centers.size(0)) ones = centers.new_ones(label.size(0)) grad_centers = centers.new_zeros(centers.size()) counts = counts.scatter_add_(0, label.long(), ones) grad_centers.scatter_add_(0, label.unsqueeze(1).expand(feature.size()).long(), diff) grad_centers = grad_centers/counts.view(-1, 1) return - grad_output * diff / batch_size, None, grad_centers / batch_size, None |
kerasも良いですが、Loss関数を自作するならPytorchの方が柔軟だと感じています。
埋め込み空間を可視化
空間に埋め込まれた特徴ベクトルip1を可視化する関数も作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def visualize(feat, labels, epoch): plt.ion() c = ['#ff0000', '#ffff00', '#00ff00', '#00ffff', '#0000ff', '#ff00ff', '#990000', '#999900', '#009900', '#009999'] plt.clf() for i in range(10): plt.plot(feat[labels == i, 0], feat[labels == i, 1], '.', c=c[i]) plt.legend(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], loc = 'upper right') plt.xlim(xmin=-8,xmax=8) plt.ylim(ymin=-8,ymax=8) plt.text(-7.8,7.3,"epoch=%d" % epoch) # plt.savefig('./images/epoch=%d.jpg' % epoch) plt.draw() plt.pause(0.001) |
可視化は推論フェーズでは不要になりますが、Center Lossの評価やハイパーパラメータを調整するのに便利なので、可視化をオススメしておきます。
学習用の関数
学習用の関数まで作成したら、前準備完了です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def train(epoch): print("Training... Epoch = %d" % epoch) ip1_loader = [] idx_loader = [] for i,(data, target) in enumerate(train_loader): data, target = data.to(device), target.to(device) ip1, pred = model(data) loss = nllloss(pred, target) + loss_weight * centerloss(target, ip1) optimizer4nn.zero_grad() optimzer4center.zero_grad() loss.backward() optimizer4nn.step() optimzer4center.step() ip1_loader.append(ip1) idx_loader.append((target)) feat = torch.cat(ip1_loader, 0) labels = torch.cat(idx_loader, 0) visualize(feat.data.cpu().numpy(),labels.data.cpu().numpy(),epoch) |
epoch毎に空間に埋め込んだ特徴ベクトルを可視化するので、train()からvisualize()を呼びます。
GPU/CPU設定
Pytorchでは、GPU/CPUどちらを使用するかの設定が必要です。なので、GPUが使用可能な環境ならGPUを使用し、そうでない場合はCPUを使用するようにします。
|
1 2 3 4 |
use_cuda = torch.cuda.is_available() and True device = torch.device("cuda" if use_cuda else "cpu") |
MNISTデータセットをダウンロード
MNISTデータセットをダウンロードします。
|
1 2 3 4 5 |
# Dataset trainset = datasets.MNIST('../MNIST', download=True,train=True, transform=transforms.Compose([ transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])) train_loader = DataLoader(trainset, batch_size=128, shuffle=True, num_workers=4) |
今回は割愛しますが、Siamese記事と同じように訓練データを可視化するのも良いかと。
学習
モデル/損失関数(Loss関数)/オプティマイザ(今回はSGD)/スケジューラ(必須ではない)を設定して、学習します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# Model model = Net().to(device) # NLLLoss nllloss = nn.NLLLoss().to(device) #CrossEntropyLoss = log_softmax + NLLLoss # CenterLoss loss_weight = 1 centerloss = CenterLoss(10, 2).to(device) # optimzer4nn optimizer4nn = optim.SGD(model.parameters(),lr=0.001,momentum=0.9, weight_decay=0.0005) sheduler = lr_scheduler.StepLR(optimizer4nn,20,gamma=0.8) # optimzer4center optimzer4center = optim.SGD(centerloss.parameters(), lr =0.5) for epoch in range(100): sheduler.step() # print optimizer4nn.param_groups[0]['lr'] train(epoch+1) |
※ハイパーパラメータλをloss_weightと定義しています
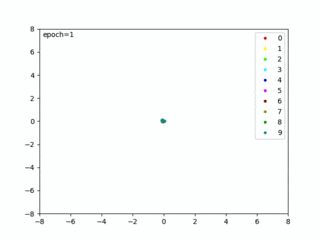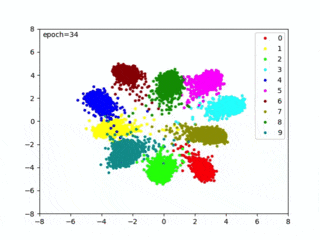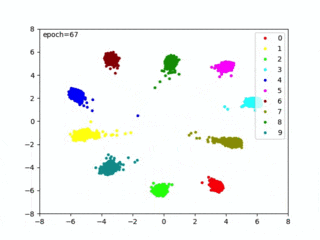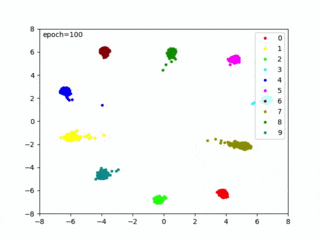
本コード実行すると、CNNから出力された特徴ベクトルip1が可視化され、距離が最適な埋め込み空間を生成する様子を確認できます(改めて、概要図を以下に置いておきます)

以上で実践も完了です。
まとめ
Center Lossの理論から実践まで徹底解説してみました。
Center LossはSiameseやTriplet Loss(本サイトで紹介してない)と違い、以下の点がスマートだと感じました。
- ペア画像のラベル付けが不要
- 従来のCNNとSoftmax LossにCenter Lossを組み込むだけで使える
- 中心(Center)の更新も簡単
- ハイパーパラメータλでCenter Lossの影響を調整可能
アルゴリズムが面白いのに加え、シンプルで扱いやすいのが、とても良いですね。
数式を交えた理論の説明は、難しくなりがちですが、図を多く使った丁寧な説明により、”スッと”理解できることを期待して書き上げました。
まとめるの大変でしたが、本記事を読んでくれた多くの人が…
など、モチベーションが向上するような感想を抱いてくれたら嬉しく思います。

























