こんにちは!
元制御屋の”はやぶさ”@Cpp_Learningです。
以前、機械学習未使用で時系列データを分析する方法について記事を書きました。
今回は、機械学習未使用シリーズ第2弾『信号処理で外れ値検出(異常検知)』について書きました。
Contents
本記事を書くモチベーション
信号処理を学ばずに、機械学習の知識を習得した人だと「時系列データの異常検知」を実現する手段が”機械学習”一択になっている気がします。
ケースバイケースですが…
と思うときがあります。
機械学習の適用が目的なら問題ありませんが、もし信号処理の知識がなくて、解決手段の選択肢が狭くなっているとしたら…誰かが教えてあげないと!
微力ではありますが、元制御屋の”はやぶさ”が皆様の勉強をサポートさせて頂きます。本記事をきっかけに…
という人や
という人が増えると嬉しいなぁ(*・ω・)ノ♪
時系列データの異常検知(外れ値検出)とは
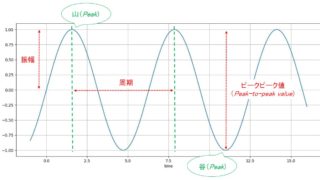
時系列データの異常には、様々なタイプがあります。本記事では下図のような、異常(外れ値)を扱います。
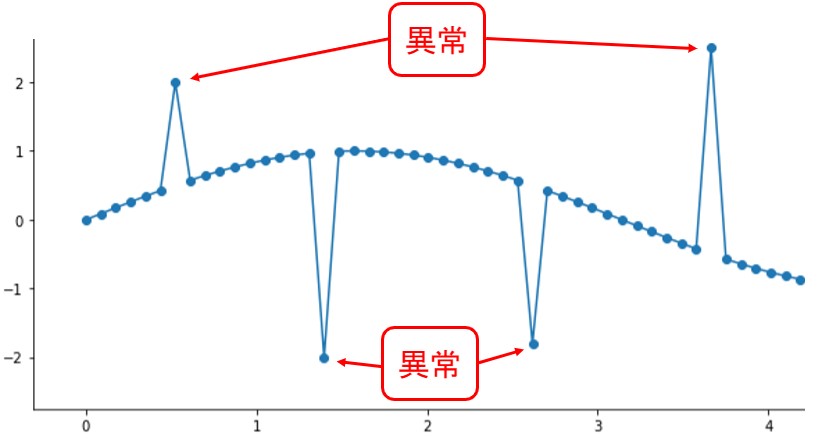
※瞬間的に大きな信号が入ることをスパイク(スパイク信号・スパイクノイズ)と呼びます
このような外れ値(スパイク)の検出に、機械学習ではなく信号処理のフィルタを適用したいと思います。
外れ値を検出できるフィルタ -Hampelフィルタ-
入力信号の外れ値(スパイク)を検出・排除できるフィルタの代表はHampelフィルタとMedianフィルタです。
本記事ではHampelフィルタを採用します。
Hampelフィルタの特徴
Hampelフィルタによる外れ値検出のアルゴリズムについて説明します。
- 窓サイズ(フィルタを適用するプロット数)を設定
- 窓内のプロット値から中央値を算出
- 中央絶対偏差を用いて、中央値に対する標準偏差を推定
- プロット値が標準偏差のn倍より大きい場合は、中央値に置き換える※
※デフォルトだとn=3(標準偏差の3倍)を使用
上記の説明で、機械学習や統計を学んだ人は”ピン”ときたかもしれません。
データを小さく(窓サイズ)で区分けして、3σ法で外れ値を検出するのがHampelフィルタの特徴です。
本記事は、信号処理入門したい人にも読んでもらいたいので、以降から信号処理の基礎について説明します。
信号処理入門
Hampelフィルタを例に信号処理の基礎について説明します。
フィルタとは
信号処理・画像処理・制御工学などで”フィルタ”という用語をよく使います。
フィルタの役割を『入力信号を変換させること』と説明する人がいます。そういった一面があることも否定できませんが…
フィルタの基本的な考えは『要らない情報を検出・排除し、欲しい情報のみ通過させる』です。
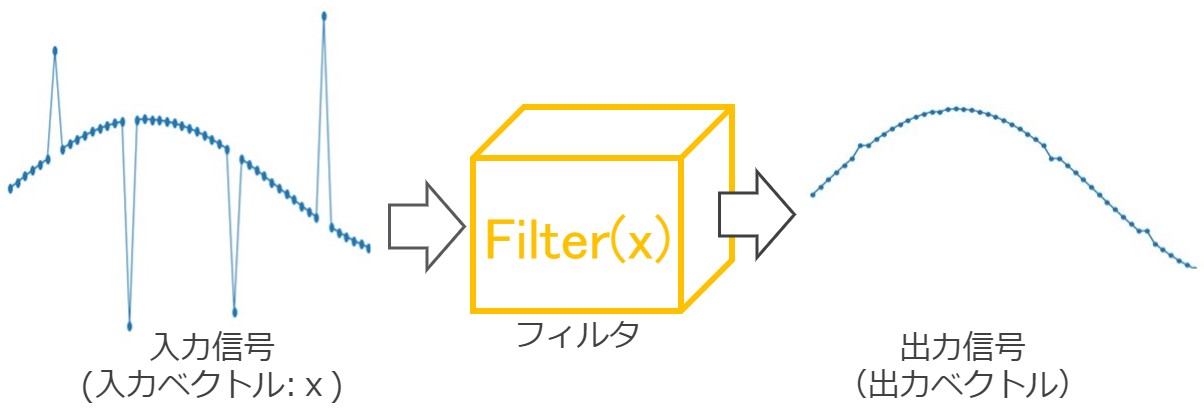
上図はHampelフィルタの例ですが、入力信号に含まれる外れ値(スパイク)をフィルタで検出・排除し、フィルタに引っかからなかった値は、そのまま通過させています。
フィルタの役割:要らない情報を検出・排除し、欲しい情報のみ通過させる
フィルタ設計
大事なことなので繰り返しますが、フィルタの役割は『要らない情報を検出・排除し、欲しい情報のみ通過させる』です。
色々と勉強し、画像処理や信号処理でフィルタ関数を使うようになると、入力値と全然違う出力値が得られる場合があるため、勘違いしそうになりますが…
基本的な考え方は、空気清浄機やマスクの”フィルタ”と同じで『フィルタでゴミをキャッチして、綺麗な空気は通過させる』というイメージです。
続いて、どんなゴミをキャッチしたいか?・どうやってキャッチするか?を考えてみます。
例えば、PM2.5などの小さな物質もキャッチするなら、どんなフィルタ(網目)を使えばキャッチできるか?を検討します。

信号処理の場合、入力信号はベクトル(画像処理なら行列)で表現できるため、以下ことを検討して、フィルタ設計をします。
- 入力ベクトルからどんな値を検出するか?
- どんなアルゴリズムで検出するか?
- 検出した値をどう排除するか?
Hampelフィルタ設計の場合は以下の通り
- 入力ベクトルに含まれる外れ値(スパイク)が検出対象
- 窓ごとに3σ法を適用して、外れ値(スパイク)を検出
- 検出した値を窓ごとの中央値に置き換える
既存のフィルタで対象(外れ値など)を検出できない場合は、上記した【フィルタ設計❶~➌】の3ステップで独自フィルタを設計することになります。
- 入力信号はベクトルで表現できる
- 3ステップでフィルタ設計
窓サイズ(ウィンドウサイズ)とは
ここまでの説明で”窓”という単語を使ってきました。窓とは下図の黄枠のことです。
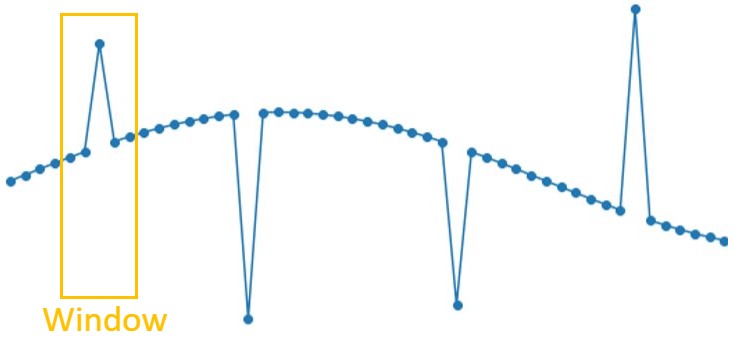
フィルタ処理の多くは、入力信号(入力ベクトル)の全パラメータに対し、同時に演算するのではなく、窓と呼ばれる単位で区分けし、窓ごとに演算します。
上図の例では、窓サイズが5プロット/窓で区分けされています(窓サイズは入力信号や検出対象次第で設定変更します)
(画像処理のフィルタだと、窓サイズ以外にカーネルサイズ3×3などと表現する場合があります)
- 入力信号を小さく区分けしたものを”窓”と呼ぶ
- 窓ごとにフィルタ処理することが多い
- 窓サイズは任意に設定できる場合が多い
- (画像処理のフィルタだと窓ではなくカーネルと表現するときもある)
実践!Hampelフィルタ設計
既に説明した通りですが、データを小さく(窓サイズ)で区分けして、3σ法で外れ値(スパイク)を検出するのがHampelフィルタの特徴です。
以下がHampelフィルタによる外れ値検出アルゴリズムの図解です。
❶ 窓サイズを設定(以下の例では5プロット/窓)

❷ 窓内のプロット値から中央値を算出
➌ 中央絶対偏差を用いて、中央値に対する標準偏差を推定
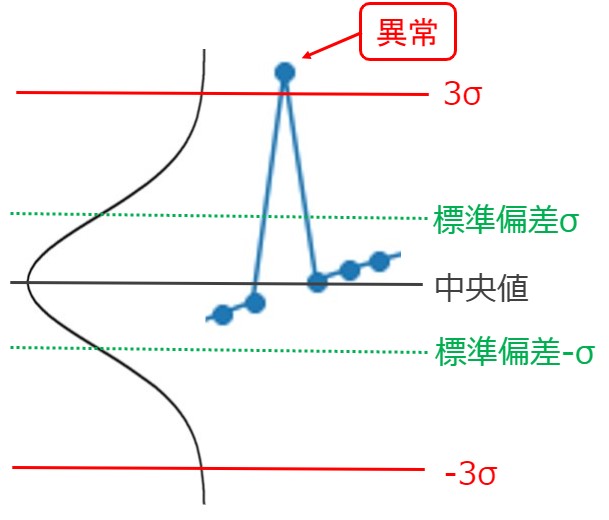
❹ プロット値が標準偏差の3倍より大きい場合は、中央値に置き換える
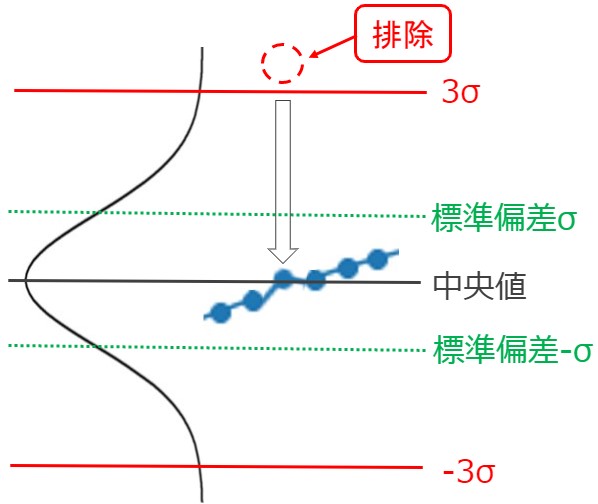
窓を少しずつ移動させながら❶~❹の処理を繰り返し、全データ(入力ベクトル)の外れ値を検出・排除します。
- 中央値以外を使う場合もあります
- 基本的には3σ基準で外れ値検出しますが、2σなどに調整する場合もあります
Hampelフィルタのソースコード作成
フィルタの検討・設計ができたら、ソースコードを作成してます。Hampelフィルタ関数は以下の通りです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
import numpy as np ''' * Input * x input data * k half window size (full 2*k+1) * thr threshold (defaut 3), optional * Output * output_x filtered data * output_Idx indices of outliers ''' def Hampel(x, k, thr=3): arraySize = len(x) idx = np.arange(arraySize) output_x = x.copy() output_Idx = np.zeros_like(x) for i in range(arraySize): mask1 = np.where( idx >= (idx[i] - k) ,True, False) mask2 = np.where( idx <= (idx[i] + k) ,True, False) kernel = np.logical_and(mask1, mask2) median = np.median(x[kernel]) std = 1.4826 * np.median(np.abs(x[kernel] - median)) ''' print("mask1 =", mask1) print("mask2 =", mask2) print("kernel =", kernel.astype(int)) print("x[kernel] =", x[kernel]) print("median =", median) print("std =", std) print("") ''' if np.abs(x[i] - median) > thr * std: output_Idx[i] = 1 output_x[i] = median # return output_x, output_Idx.astype(bool) return output_x, output_Idx |
実践!Hampelフィルタで外れ値検出(異常検知)
Hampelフィルタを適用し、入力信号の外れ値検出(異常検知)を実践してみます。
入力信号を用意
正弦波+スパイクの入力信号を用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np import matplotlib.pyplot as plt # sin波を用意 t = np.arange(0, 2*np.pi, np.pi/36) x = np.sin(t) # 外れ値を挿入 x[6] = 2 x[16] = -2 x[30] = -1.8 x[42] = 2.5 x[60] = -2.5 plt.plot(t, x, marker="o") plt.title('Input Signal') plt.xlabel('t') plt.ylabel('x') plt.grid() plt.show() |
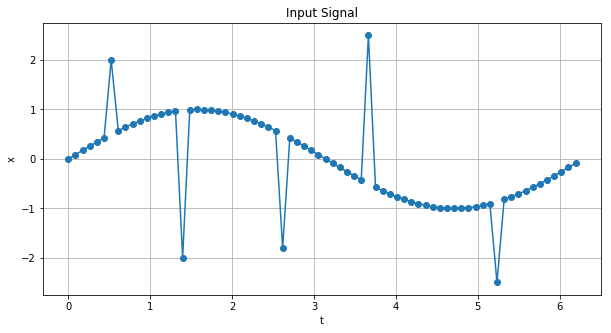
このコードで上図の入力信号:xを生成しました。
フィルタ処理
今回は以下の設定でフィルタ処理します。
- 窓サイズ:5 ( 2 * k + 1, k = 2)
- 閾値:3σ (thr = 3)
以下のコードで入力信号:xにフィルタ処理します。
|
1 2 3 |
result = Hampel(x, k=2, thr=3) print('Filtered Signal =', result[0]) print('Index =', result[1]) |
フィルタ処理後の出力結果は以下の通りです。
- Filtered Signal(result[0]):フィルタ処理後の出力信号
- Index(result[1]):外れ値を検出した位置(x[6]検知など)
Filtered Signal = [ 0 0.08 0.17 … -0.26 -1.74 -0.09 ]
Index = [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
出力信号を可視化
以下のコードで入力信号:xと出力信号:result[0]を重ねて描画します。
|
1 2 3 4 5 6 7 8 |
plt.plot(t, x, marker="o", label = 'Input signal') plt.plot(t, result[0], linewidth = 2.0,label = 'Filtered signal') plt.title('Hampel Filter') plt.xlabel('t') plt.ylabel('x') plt.legend() plt.grid() plt.show() |
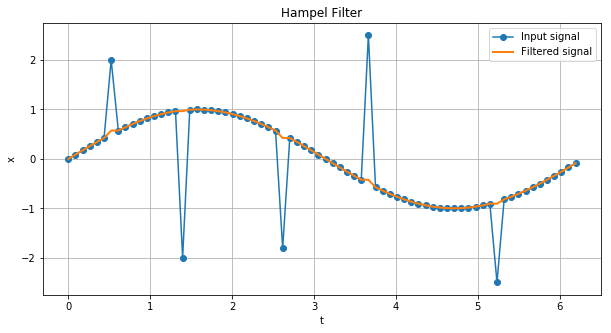
Hampelフィルタを適用により、外れ値(スパイク)の検出・排除ができました。
現場で扱う信号が今回のような単純なものとは限りませんが、機械学習を使用せず、信号処理のフィルタのみで外れ値検出(異常検知)できる場合もあります。
もし、信号処理のみで異常検知できない場合でも、フィルタ処理後の検出結果や出力信号を特徴量とし、機械学習と組み合わせることで課題解決できることもあります。
- 信号処理のみで異常検知ができる場合がある
- フィルタ処理後の検出結果や出力信号は特徴量として使える
信号処理で外れ値検出(異常検知)まとめ
機械学習による異常検知が流行っていますが、信号処理でも異常検知(外れ値検出)ができることを知ってほしくて本記事を書きました。
Hampelフィルタによる外れ値検出の説明だけでも良かったのですが…
信号処理入門したい人を後押ししたかったので、以下の項目について丁寧に説明しました。
- 信号処理の基本
- フィルタの検討・設計のやり方
- フィルタ実装(ソースコード)
- 信号処理による外れ値検出の実践
機械学習の勉強は楽しいですか?覚えるアルゴリズムが多くて大変ですか?
頑張って機械学習ちょっと分かるレベルになった人は、信号処理技術も習得しませんか?
本記事をきっかけに信号処理をもっと勉強したい!という人が現れたら最高に嬉しいです!
時間がある人は以下も読んでみてね(*・ω・)ノ♪
おまけ -記事の紹介-
「本記事を書くモチベーション」で説明しましたが、本記事は機械学習より信号処理が良い!という内容ではなく…
異常検知などの課題解決に信号処理も使えるよ!機械学習以外の解決手段も増やしてほしい!と想って書きました。
同様の想いで以下の記事(機械学習未使用シリーズ第1弾)も書きました。

この記事は機械学習だけでなく、振動解析(フーリエ解析)という手段を増やしてほしい!という内容です。
また、最近読んだモータ制御マンさん@motorcontrolmanの記事が個人的に大ヒットでした!
この記事の内容を一部引用します。
統計学の専門家と制御屋との溝は案外深く、これは文化的な違いによるものと思います。お互いが歩み寄れればもっとよい製品、もっとよいサービスの実現に繋がると思いますので、この記事が相互理解の助けになれば幸いです(今更)
(略)
「どのフィルタを使うべきか」はエンジニアの腕の見せ所と思います。移動平均フィルタやローパスフィルタを冷遇することなく、場面に合わせて使い分けられるこなせる事こそがチョットデキルエンジニアとしての理想ではないでしょうか。
完全に同意です。
あらゆる専門分野の理解を深め、課題に応じて最適な技術を選択あるいは組み合わせを検討できるエンジニアはとてもカッコイイと思います(*・ω・)ノ♪
本記事が『信号処理による異常検知や特徴量生成』を実践するときのヒントや課題解決の選択肢を広げるきっかけになれば嬉しく思います。









![[新刊] 機械学習の炊いたん2。](https://cpp-learning.com/wp-content/uploads/2019/10/Taitan2-e1570628999904-320x180.jpg)











