こんにちは。
現役エンジニアの”はやぶさ”@Cpp_Learningです。最近は統計モデリングを勉強しています。
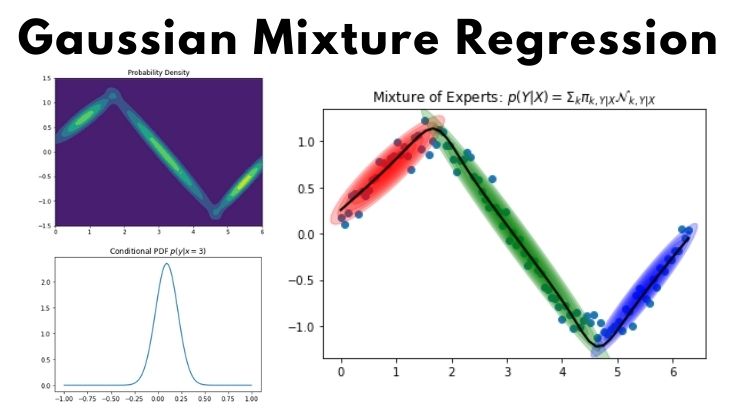
今回はGMR(Gaussian Mixture Regression)について勉強したので、備忘録も兼ねて本記事を書きます。
Contents
ベイズ統計モデリングに関する用語集
本記事に登場する用語を簡単に整理します。
- 確率分布:確率変数 x の確率分布は P(x) と書く
- 同時分布:確率変数 x, y など複数の場合、同時分布(確率分布の一種)は P(x, y) と書く
- 条件付き確率分布:同時分布 P(x, y) について、y=1 など特定の値が与えれたときの確率変数 x の確率分布を P(x|y=1) と書く※
- ベイズの定理:原因 x から結果 y が得られる確率を P(y|x) と考えたとき、この確率などを用いて、結果 y から原因 x が得られる確率 P(x|y) を算出する定理
- ガウス混合モデル:あるデータが複数のガウス分布を混ぜたような分布に従うとき、ガウス混合モデル(GMM:Gaussian Mixture Model)を使うことで、各分布に所属するデータにクラスタリングができる
※P(x|y)と書く場合は、yが変数ではなく特定の値であることを明示している
本記事では各用語どうしの関連や数式などの詳細を割愛しますが、以下の書籍が非常に参考になるので、是非読んで頂きたいです。
書籍以外では、以下の記事が参考になります。
GMR(Gaussian Mixture Regression)とは
GMR(Gaussian Mixture Regression)とは、ガウス混合モデル (GMM:Gaussian Mixture Models) をクラスタリングだけでなく、回帰分析にも活用する手法です。
簡易フローは以下の通りです。
- GMMより、同時分布p(x, y)を算出
- p(x, y)とベイズの定理より、条件付き確率p(y|x)を算出
詳細については、以下の資料が参考になります。
【GMMについて】
【GMRについて】
実践!GMR(Gaussian Mixture Regression)
ここまでの説明でGMRが何なのか理解できない人もいると思いますが…
以降のGMR実践で具体的なイメージを確認してから、本記事で紹介した資料を読むと理解が捗ると思います。
インストール
sklearn で GMM によるクラスタリングはできますが GMR(回帰)は未サポートなので、今回は gmr|Github を使います。
以下のコマンドでインストールします。
pip install gmr
Google Colab を使う場合はこれだけで準備完了です。
本記事で紹介するソースコードは Google Colab で動作確認しました
import
最初はimportから
|
1 2 3 4 5 |
import matplotlib.pyplot as plt import numpy as np from gmr import GMM, plot_error_ellipses from gmr.utils import check_random_state |
サンプル用意
適当なサンプルを用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# Generate dataset n_samples = 100 random_state = check_random_state(0) X = np.ndarray((n_samples, 2)) X[:, 0] = np.linspace(0, 2 * np.pi, n_samples) X[:, 1] = np.sin(X[:, 0]) + random_state.randn(n_samples) * 0.1 # Visualize plt.scatter(X[:, 0], X[:, 1]) plt.title("Samples") plt.show() |
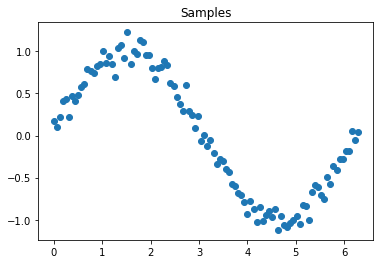
今回はSinカーブにノイズを混ぜたデータを使います(上図参照)。
GMM -モデル設計-
今回はクラスタ数が3個のガウス混合モデル(GMM)を使います。
|
1 2 |
gmm = GMM(n_components=3, random_state=0) gmm.from_samples(X) |
sklearn とほとんど同じコードが使えます。ただし fit() ではなく、from_samples() を使います。
GMMの可視化
plot_error_ellipses() を使い、GMM(クラスタリング結果)を可視化します。
|
1 2 3 4 5 6 7 |
COLOR_LIST = ["r", "g", "b"] ax = plt.gca() plot_error_ellipses(ax, gmm, colors=COLOR_LIST) plt.scatter(X[:, 0], X[:, 1], s=40, zorder=2) plt.title("Gaussian Mixture Model") plt.show() |
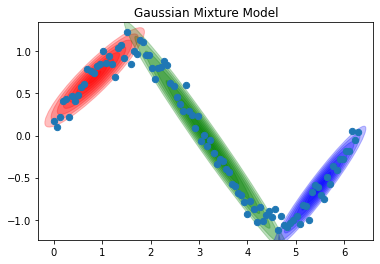
綺麗にクラスタリングできました。このときの同時分布 P(x, y) は2次元ガウス分布なので、P(x, y) = この確率密度関数 で表現できます。
確率密度関数(ガウス分布)を等高線で可視化
以下のコードで確率密度関数 P(x,y) を可視化できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Generate grid point (80 * 40 point) x, y = np.meshgrid(np.linspace(0, 6, 80), np.linspace(-1.5, 1.5, 40)) Grid_point = np.vstack((x.ravel(), y.ravel())).T # Compute probability density (Compute height for grid point) p = gmm.to_probability_density(Grid_point) p = p.reshape(*x.shape) # Visualize grid point plt.figure(figsize=(15, 5)) plt.subplot(1, 2, 1) plt.scatter(Grid_point[:, 0], Grid_point[:, 1], s=3) plt.title("Grid point") # Visualize Probability Density plt.subplot(1, 2, 2) plt.contourf(x, y, p) plt.title("Probability Density") plt.show() |
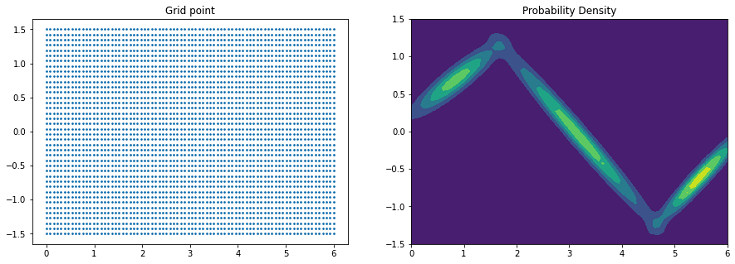
左図の格子点(x, y)ごとの P(x, y) を算出し、数値の大きさに応じた色付けにより、2次元ガウス分布を等高線で可視化しています(右図参照)。
ソースコード 2行目で格子点の数を調整できます。格子点を増やせば、より滑らかな等高線を描けます。
条件付き確率の算出と可視化
条件付き確率 p(y | x=3) を算出して可視化します。これは『x=3 を与えたときの y の確率を予測する』と考えても良いです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Axis x_axis, y_axis = np.array([0]), np.array([1]) # Test data test_x, test_y = np.array([3.0]), np.array([-0.5]) # Compute conditional distribution over given indices. y_cond = gmm.condition(x_axis, test_x) # p(y | x = 3) # x_cond = gmm.condition(y_axis, test_y) # p(x | y = -0.5) # Generate Grid point (x axis) Grid_X = np.linspace(-1, 1, 100) # Compute probability density (Compute height for grid point) Y_cond = y_cond.to_probability_density(Grid_X[:, np.newaxis]) # Visualize Conditional PDF plt.plot(Grid_X, Y_cond) plt.title("Conditional PDF $p(y | x = 3)$") plt.show() # Output print(" ==== y_cond.means ==== ") print(y_cond.means) # print(" ==== x_cond.means ==== ") # print(x_cond.means) |
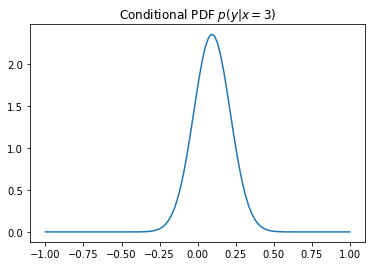
μ=0.09459223(以降 μ[3] と呼ぶ)の分布が予測できました。つまり『x=3 のとき y は上記の分布に従い μ[3] 付近でばらつく』と予測できました。
GMR -GMMを活用した回帰-
p(y | x=3) 同様に、x=n のときの p(y | x=n) を算出し、条件付き確率ごとの μ[n] から回帰分析を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# Test data X_test = np.linspace(0, 2 * np.pi, 50) # Predict Y = gmm.predict(np.array([0]), X_test[:, np.newaxis]) # Visualize GMR plot_error_ellipses(plt.gca(), gmm, colors=COLOR_LIST) plt.plot(X_test, Y.ravel(), c="k", lw=2) plt.scatter(X[:, 0], X[:, 1]) plt.title("Mixture of Experts: $p(Y | X) = \Sigma_k \pi_{k, Y|X} \mathcal{N}_{k, Y|X}$") plt.show() |
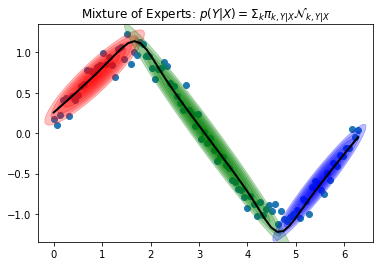
今回は適当なデータ(X_test)50個に対応する Y を予測し、黒線で予測結果を可視化しました。綺麗な回帰曲線になってますね。
まとめ
GMR(Gaussian Mixture Regression)について勉強した内容をまとめました。
本記事の内容について間違っている箇所があれば、教えて頂けると嬉しいです。
ベイズ統計モデリングは難しいけど、強力な武器になると感じた(それに奥が深くて面白い)ので、今後も勉強した内容を記事にしたいと考えています。
以下 本記事の前半で紹介したオススメの書籍を改めて載せておきます。