こんにちは。現役エンジニアの”はやぶさ”@Cpp_Learningです。
最適化問題を気軽に解くための最適化フレームワーク:codable-model-optimizer が非常に魅力的だったので、回帰モデルのパラメータ調整を題材に、使い方を解説します。
Contents
Codable Model Optimizerとは
Codable Model Optimizer に興味ある人は、Recruit Data Blog にある以下の公式ブログ記事を必ず読んでほしいです!
私自身の言葉で Codable Model Optimizer について、あれこれ書くことも考えましたが、蛇足だと判断しました。なので本記事では、公式ブログには無い「実用例」の説明に注力して書きます。
実践!Codable Model Optimizer
Codable Model Optimizer による「回帰モデルのパラメータ自動調整」について説明します。
正確には「回帰モデルの評価指標の1つである、決定係数(R2)が最大となるパラメータをCodable Model Optimizer で算出する」という表現が適切です。
インストール
以下のコマンドでインストールします。
pip install codableopt
依存ライブラリは numpy のみです。なので最低限の動作環境は以下の通りです。
- Python >= 3.8
- codableopt == 0.1.2
- numpy >= 1.22.0
以降からソースコード書いていきます。
Import
まずはimportから
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np import matplotlib.pyplot as plt from sklearn.metrics import mean_squared_error, r2_score from codableopt import Problem, Objective from codableopt import DoubleVariable # from codableopt import IntVariable, DoubleVariable, CategoryVariable from codableopt import OptSolver, PenaltyAdjustmentMethod np.random.seed(0) |
説明変数と目的変数
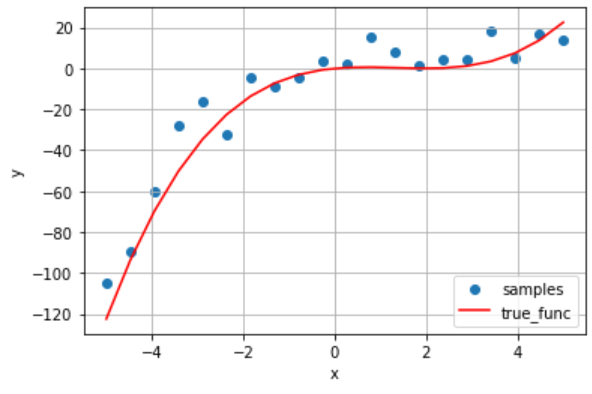
適当な説明変数と目的変数を用意します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# データ数 N = 20 # 真の関数 def true_func(x): y = 2 * x - 2 * (x ** 2) + 0.5 * (x ** 3) return y # 説明変数 x = np.linspace(-5, 5, N) # x = np.random.uniform(-5, 5, N) # 目的変数 y = true_func(x) + np.random.normal(loc=0, scale=10, size=N) # 可視化 plt.scatter(x, y, label="samples") plt.plot(x, true_func(x), color="r", label="true_func") plt.xlabel('x') plt.ylabel('y') plt.legend(loc="lower right") plt.grid() plt.show() |
Problemオブジェクト作成
Problemオブジェクトを生成します。引数が is_max_problem=True の場合は最大化問題、False の場合は最小化問題です。
|
1 2 |
# set problem problem = Problem(is_max_problem=True) |
目的関数の設定
目的関数:y = b0 + b1x + b2x^2 + b3x^3 の最適値を算出します。正確には R2 を最大化するパラメータ b0~b3 を算出します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# define model def model(b0, b1, b2, b3, x): y_pred = b0 + b1*x + b2*x**2 + b3*x**3 return y_pred # define objective function def objective_function(b0, b1, b2, b3, X, Y): Y_pred = [] for x in X: y_pred = model(b0, b1, b2, b3, x) Y_pred.append(y_pred) # rmse = np.sqrt(mean_squared_error(Y, Y_pred)) r2 = r2_score(Y, Y_pred) # return rmse return r2 |
最適化で利用する変数を定義
最適化で利用する各パラメータ b0~b3 が上下限-5.0~5.0の範囲の連続値だと定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# define variables b0 = DoubleVariable(name='b0', lower=np.double(-5.0), upper=np.double(5.0)) b1 = DoubleVariable(name='b1', lower=np.double(-5.0), upper=np.double(5.0)) b2 = DoubleVariable(name='b2', lower=np.double(-5.0), upper=np.double(5.0)) b3 = DoubleVariable(name='b3', lower=np.double(-5.0), upper=np.double(5.0)) # arguments args_map = { 'b0': b0, 'b1': b1, 'b2': b2, 'b3': b3, 'X': x, 'Y': y, } # set objective function and its arguments problem += Objective( objective=objective_function, args_map=args_map ) print(problem) |
「チューニング対象のパラメータが連続値で、探索範囲を-5.0~5.0に設定」という表現の方が分かりやすいかも。
最適化の実行
ソルバーオブジェクトと最適化手法オブジェクトを生成し、最適化計算を行います。
|
1 2 3 4 5 6 7 8 9 10 |
# ソルバーを生成 solver = OptSolver() # 最適化手法を生成 # generate optimization methods to be used within the solver method = PenaltyAdjustmentMethod(steps=10000) # 最適化実施 answer, is_feasible = solver.solve(problem, method) print(f'answer:{answer}, answer_is_feasible:{is_feasible}') |
answer:{‘b0’: 4.9598541557333915, ‘b1’: 2.468429435349079, ‘b2’: -1.9206374732463405, ‘b3’: 0.40126042390510896}, answer_is_feasible:True
回帰モデルとR2の評価
算出した回帰モデルのR2評価と可視化を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
y_pred = model(answer['b0'], answer['b1'], answer['b2'], answer['b3'], x) r2 = objective_function(answer['b0'], answer['b1'], answer['b2'], answer['b3'], x, y) print("r2:", r2) # 可視化 plt.scatter(x, y, label="samples") plt.plot(x, y_pred, color='g', label="model") plt.plot(x, true_func(x), color="r", label="true_func") plt.xlabel('x') plt.ylabel('y') plt.legend(loc="lower right") plt.grid() plt.show() |
r2: 0.9529992755681892
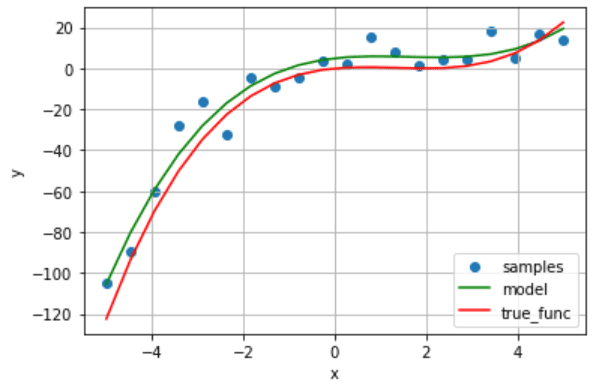
以上 Codable Model Optimizer による「回帰モデルのパラメータ自動調整」の解説でした。
まとめ
最適化フレームワーク:codable-model-optimizer について、簡単な「実用例」を交えて紹介しました。開発者が意図した通り、最適化ソルバーを簡単に利用できました。
なお本記事で紹介できなかった機能もありますので、公式ドキュメントを是非チェックしてみてください。
以下 オススメのPython書籍を紹介。




















